DFS（二）岛屿问题合集

news2024/9/29 17:34:44

目录

一、 463. 岛屿的周长

二、 130. 被围绕的区域

三、 200. 岛屿数量

四、695. 岛屿的最大面积

一、463. 岛屿的周长

给定一个 row x col 的二维网格地图 grid ，其中：grid[i][j] = 1 表示陆地， grid[i][j] = 0 表示水域。

网格中的格子 水平和垂直 方向相连（对角线方向不相连）。整个网格被水完全包围，但其中恰好有一个岛屿（或者说，一个或多个表示陆地的格子相连组成的岛屿）。

岛屿中没有“湖”（“湖” 指水域在岛屿内部且不和岛屿周围的水相连）。格子是边长为 1 的正方形。网格为长方形，且宽度和高度均不超过 100 。计算这个岛屿的周长。

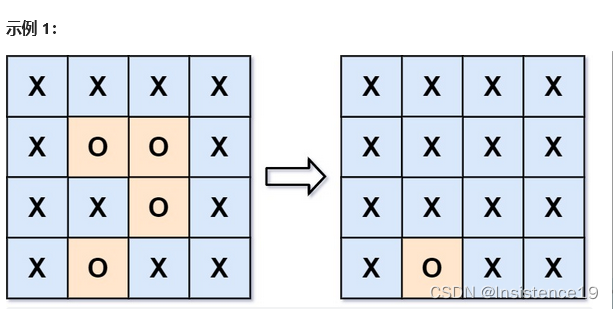
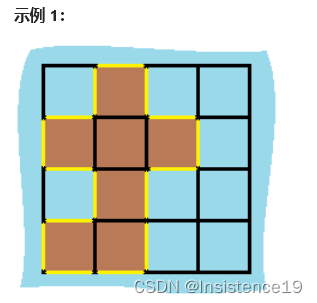
示例 1：

输入：grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]]
输出：16
解释：它的周长是上面图片中的 16 个黄色的边

 【解法一】

        //随便找到第一个1的位置判断它的四面环绕情况
        // 从这个位置出发上下左右遍历每一块陆地
        // 遇到新的陆地并且没有走过就DFS

int nextP[4][2] = {{0,1},{0,-1},{1,0},{-1,0}};
class Solution {
public:
    int dfs(vector<vector<int>>& grid, int curX, int curY, vector<vector<bool>>& book, int row, int col)
    {
        int line = 0;
        // 如果左边是边界或者为海line++
        if(curY==0 || grid[curX][curY-1]==0)
            line++;
        if(curY==col-1 || grid[curX][curY+1]==0)
            line++;
        if(curX==0 || grid[curX-1][curY]==0)
            line++;
        if(curX==row-1 || grid[curX+1][curY]==0)
            line++;
        book[curX][curY] = true;

        for(int i = 0; i < 4; i++)
        {
            int newX = curX + nextP[i][0];
            int newY = curY + nextP[i][1];

            if(newX<0||newX>=row||newY<0||newY>=col)
                continue;//越界
            if(book[newX][newY]==false && grid[newX][newY]==1)// 新的陆地并没有走过
                line += dfs(grid, newX, newY, book, row, col);
        }
        return line;
    }

    int islandPerimeter(vector<vector<int>>& grid) {
        //随便找到第一个1的位置判断它的四面环绕情况
        // 从这个位置出发上下左右遍历每一块陆地
        // 遇到新的陆地并且没有走过就DFS
        int curX = 0;
        int curY = 0;
        int row = grid.size();
        int col = grid[0].size();
        for(int i = 0; i < row; i++)
        {
            int flag = 0;
            for(int j = 0; j < col; j++)
            {
                if(grid[i][j]==1)
                {
                    curX = i;
                    curY = j;
                    flag = 1;
                    break;
                }
            }
            if(flag==1)break;
        }
        vector<vector<bool>> book(row,vector<bool> (col, false));
        return dfs(grid, curX, curY, book, row, col);
    }
};

【解法二】数学思维

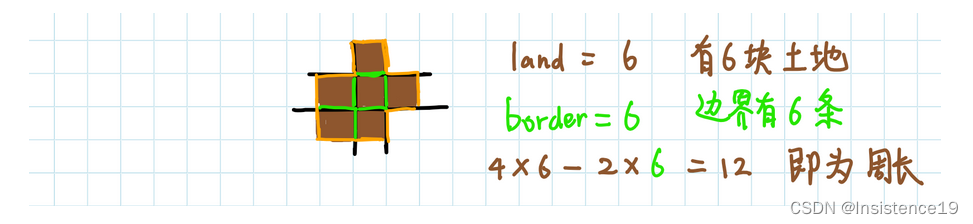
每块陆地有四条边，如果俩块陆地接壤就会少俩条边

依次从左到右从上到下遍历grid，如果遇到陆地land++，如果该陆地下或者右为陆地那么接壤+=2

class Solution {
public:
    int islandPerimeter(vector<vector<int>>& grid) {
        int row = grid.size();
        int col = grid[0].size();
        int land = 0;
        int boder = 0;
        for(int i = 0; i < row; i++)
        {
            for(int j = 0; j < col; j++)
            {
                if(grid[i][j]==1)
                {
                    land++;
                    if(i+1<row &&grid[i+1][j]==1)
                        boder++;
                    if(j+1<col &&grid[i][j+1]==1)
                        boder++;
                }
            }
        }
        return 4*land-2*boder;
    }
};

二、 130. 被围绕的区域

给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' ，找到所有被 'X' 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。

输入：board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
输出：[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
解释：被围绕的区间不会存在于边界上，换句话说，任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上，或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。

 第一个思路是for循环从（1,1）下标开始遍历，并判断是否被围绕（想想都复杂果断抛弃）

直接去在边界上找可以连通的把不被围绕的找出来重新赋值

        for(int i = 0; i < row; i++)
        {
            for(int j= 0; j < col; j++)
            {
                if(board[i][j]=='Z')
                    board[i][j] = 'O';

              // if(board[i][j]=='O')  错误！！！
                else if(board[i][j]=='O')
                    board[i][j] = 'X';
            }  又犯这个小错误，if与if进行二次判断，在第一次的结果上进行修改结果错误
        }      双if相同判断会进行数据二次修改，尽量使用else if

int nextP[4][2] = {{0,1},{0,-1},{1,0},{-1,0}};
class Solution {
public:
    void dfs(vector<vector<char>>& board, int curX, int curY, vector<vector<bool>>&book, int row, int col)
    {
        // 进行赋值为Z
        board[curX][curY] = 'Z';
        book[curX][curY] = true;

        // 进行上下左右搜索
        for(int i = 0; i < 4; i++)
        {
            int newX = curX + nextP[i][0];
            int newY = curY + nextP[i][1];

            // 越界检测
            if(newX<0||newX>=row 
            || newY<0||newY>=col)
                continue;
            // book标志位可以不用加入
            //if(book[newX][newY]==false && board[newX][newY]=='O')
            if(board[newX][newY]=='O')
                dfs(board, newX, newY, book, row, col);
        }
    }

    void solve(vector<vector<char>>& board) {
        if(board.empty())return;
        int row = board.size();
        int col = board[0].size();
        vector<vector<bool>> book(row, vector<bool>(col, false));
        for(int i = 0; i < row; i++)
        {
            if(board[i][0]=='O' && book[i][0]==false)
                dfs(board, i, 0, book,row,col);
            if(board[i][col-1]=='O'&&book[i][col-1]==false)
                dfs(board,i, col-1, book,row,col);
        }
        for(int j = 1; j < col; j++)
        {
            if(board[0][j]=='O'&&book[0][j]==false)
                dfs(board, 0, j, book,row,col);
            if(board[row-1][j]=='O'&&book[row-1][j]==false)
                dfs(board, row-1, j, book,row,col);
        }
        for(int i = 0; i < row; i++)
        {
            for(int j= 0; j < col; j++)
            {
                if(board[i][j]=='Z')
                    board[i][j] = 'O';
                else if(board[i][j]=='O') // 又犯这个小错误，if与if进行二次判断，在第一次的结果上进行修改结果错误
                    board[i][j] = 'X';
            }
        }
    }
};

 book标志位可以进行去掉，因为之前已经将走过的赋值为“Z”了，如果是重复的比如之前的题中走过了防止再重复走就使用book向量进行判断

            // book标志位可以不用加入
            //if(book[newX][newY]==false && board[newX][newY]=='O')
            if(board[newX][newY]=='O')
                dfs(board, newX, newY, book, row, col);

修改后：

int nextP[4][2] = {{0,1},{0,-1},{1,0},{-1,0}};
class Solution {
public:
    void dfs(vector<vector<char>>& board, int curX, int curY, int row, int col)
    {
        // 进行赋值为Z
        board[curX][curY] = 'Z';

        // 进行上下左右搜索
        for(int i = 0; i < 4; i++)
        {
            int newX = curX + nextP[i][0];
            int newY = curY + nextP[i][1];

            // 越界检测
            if(newX<0||newX>=row 
            || newY<0||newY>=col)
                continue;
            if(board[newX][newY]=='O')
                dfs(board, newX, newY, row, col);
        }
    }

    void solve(vector<vector<char>>& board) {
        if(board.empty())return;
        int row = board.size();
        int col = board[0].size();
        for(int i = 0; i < row; i++)
        {
            if(board[i][0]=='O')
                dfs(board, i, 0,row,col);
            if(board[i][col-1]=='O')
                dfs(board,i, col-1,row,col);
        }
        for(int j = 1; j < col; j++)
        {
            if(board[0][j]=='O')
                dfs(board, 0, j,row,col);
            if(board[row-1][j]=='O')
                dfs(board, row-1, j,row,col);
        }
        for(int i = 0; i < row; i++)
        {
            for(int j= 0; j < col; j++)
            {
                if(board[i][j]=='Z')
                    board[i][j] = 'O';
                else if(board[i][j]=='O') // 又犯这个小错误，if与if进行二次判断，在第一次的结果上进行修改结果错误
                    board[i][j] = 'X';
            }
        }
    }
};

三、 200. 岛屿数量

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

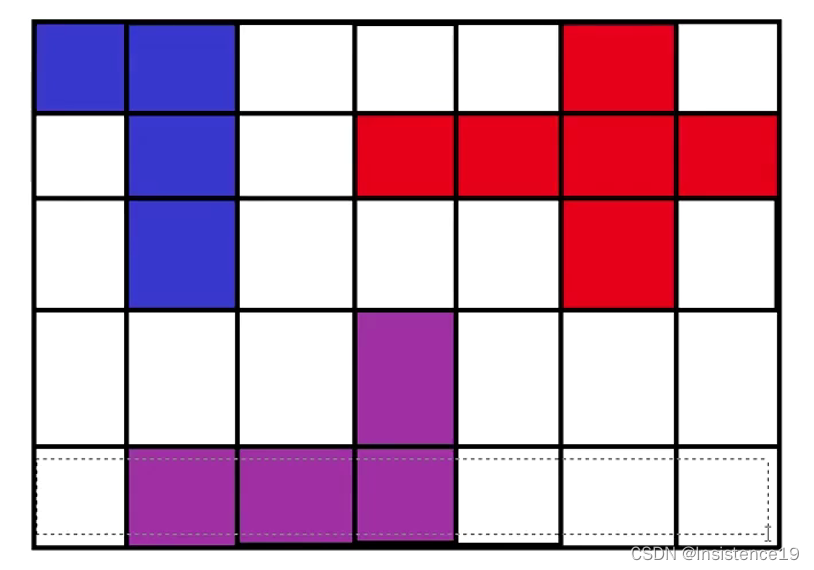
思路：遍历二维数组，遇到‘1’就进行dfs将一块岛上所有数都置为0，然后继续遍历

           每次碰到1就进行计数，然后进入dfs

int nextP[4][2] = {{0,1},{0,-1},{-1,0},{1,0}};
class Solution {
public:
    void dfs(vector<vector<char>>& grid, int curX, int curY, int row, int col)
    {
        //进行替换 1->0
        grid[curX][curY] = '0';

        // 上下左右遍历
        for(int i = 0; i < 4; i++)
        {
            int newX = curX + nextP[i][0];
            int newY = curY + nextP[i][1];

            // 检测是否越界
            if(newX<0||newX>=row
            || newY<0||newY>=col)
                continue;
            // 检测是否是‘1’
            if(grid[newX][newY]=='1')
                dfs(grid, newX, newY, row, col);
        }
    }
    int numIslands(vector<vector<char>>& grid) {
        int row = grid.size();
        int col = grid[0].size();
        int count = 0;
        for(int i = 0; i < row; i++)
        {
            for(int j = 0; j < col; j++)
            {
                if(grid[i][j]=='1')
                {
                    ++count;
                    dfs(grid, i, j, row, col);
                }
            }
        }
        return count;
    }
};

四、695. 岛屿的最大面积

给你一个大小为 m x n 的二进制矩阵 grid 。

岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

岛屿的面积是岛上值为 1 的单元格的数目。

计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。

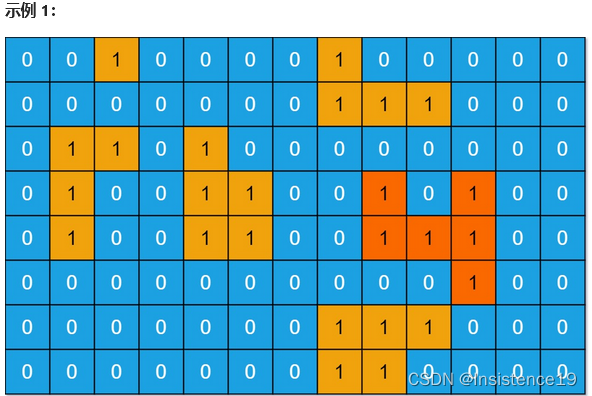
输入：grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出：6
解释：答案不应该是 11 ，因为岛屿只能包含水平或垂直这四个方向上的 1 。

 在上一个题的基础上加一个int类型的返回值以及对于maxS的判断即可。

int nextP[4][2] = {{1,0},{-1,0},{0,1},{0,-1}};
class Solution {
public:
    int dfs(vector<vector<int>>& grid, int curX, int curY, int row, int col)
    {
        int num = 0;
        num++;
        grid[curX][curY]=0;
        for(int i = 0; i < 4; i++)
        {
            int newX = curX + nextP[i][0];
            int newY = curY + nextP[i][1];
            if(newX<0||newX>=row
            || newY<0||newY>=col)
                continue;
            if(grid[newX][newY]==1)
                num += dfs(grid, newX, newY, row, col);
        }
        return num;
    }
    int maxAreaOfIsland(vector<vector<int>>& grid) {
        int row = grid.size();
        int col = grid[0].size();
        int maxS = 0;
        for(int i = 0; i < row; i++)
        {
            for(int j = 0; j < col; j++)
            {
                if(grid[i][j]==1)
                {
                    int temp = dfs(grid, i, j, row, col);
                    maxS = maxS>temp?maxS:temp;
                }
            }
        }
        return maxS;
    }
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/174481.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Java设计模式-解释器模式、解释器模式什么回事，抽象语法树又是什么

Java设计模式-解释器模式、解释器模式什么回事，抽象语法树又是什么

继续整理记录这段时间来的收获&#xff0c;详细代码可在我的Gitee仓库SpringBoot克隆下载学习使用&#xff01; 6.12 解释器模式 6.12.1 概述 思维&#xff1a;翻译识别机器&#xff0c;如解析由数字、“”、“-”号构成的合法运算序列&#xff0c;若将数字和字符看作结点&a…
阅读更多...
Lesson 4.1 逻辑回归模型构建与多分类学习方法

Lesson 4.1 逻辑回归模型构建与多分类学习方法

文章目录一、广义线性模型&#xff08;Generalized liner model&#xff09;的基本定义二、对数几率模型与逻辑回归1. 对数几率模型&#xff08;logit model&#xff09;2. 逻辑回归与 Sigmoid 函数3. Sigmoid 函数性质三、逻辑回归模型输出结果与模型可解释性四、多分类学习与…
阅读更多...
CPU缓存一致性

CPU缓存一致性

CPU缓存一致性写直达写回缓存一致性总线嗅探MESI协议CPU Cache通常分为三级缓存&#xff0c;L1Cache&#xff0c;L2Cache,L3Cache&#xff0c;级别越低的离CPU越近&#xff0c;访问速度越快&#xff0c;但同时容量越小&#xff0c;价格越贵。在多核的CPU中&#xff0c;每个核都…
阅读更多...
今天大年三十，新年快乐，我在这里给大家整理了一下除夕的习俗，来看看吧

今天大年三十，新年快乐，我在这里给大家整理了一下除夕的习俗，来看看吧

今天是大年三十，阿玥在这里祝大家，一来风水，二来平安，阖家欢乐，四季平安，五福临门，六六大顺，七星高照，八方来财，十全十美，新年好！ 名字：不晓得 学习：python，c 主页：木有 今天给大家整理一下大年三十的习俗等小知识，就不更python啦 目录 除夕要做的事情有什么…
阅读更多...
Meta CTO：真正的全天候轻量化AR眼镜，可能要到2030年

Meta CTO：真正的全天候轻量化AR眼镜，可能要到2030年

去年Meta发布了售价高达1500美元的VST头显Quest Pro&#xff0c;该头显与Meta的Quest 2等产品在定价、技术路径上有很大不同&#xff0c;其搭载了眼球追踪、彩色VST等更高端的功能&#xff0c;而产品发布后&#xff0c;外界对其反馈也褒贬不一。作为Pro产品线首个产品&#xff…
阅读更多...
Markdown基础总结

Markdown基础总结

Markdown Tools TyporaVSCode Markdown Preview Enhanced扩展 有道云笔记… 上述工具都能很好地支持markdown书写 Markdown标题 1 使用 和 - 标记一级和二级标题 和 - 标记语法格式如下&#xff1a; 我展示的是一级标题我展示的是二级标题 ---效果如下: 2 使用 # 号标…
阅读更多...
Java设计模式-访问者模式、访问者模式怎么使用，具体是怎么用

Java设计模式-访问者模式、访问者模式怎么使用，具体是怎么用

继续整理记录这段时间来的收获&#xff0c;详细代码可在我的Gitee仓库SpringBoot克隆下载学习使用&#xff01; 6.10 访问者模式 6.10.1 定义 封装一些作用域某种数据结构中的各元素的操作&#xff0c;可以在不改变此数据结构的前提下定义作用于这些元素的新操作 6.10.2 结…
阅读更多...
2023年新年烟花代码（背景音乐完整版）

2023年新年烟花代码（背景音乐完整版）

文章目录前言烟花效果展示使用教程查看源码HTML代码CSS代码JavaScript新年祝福前言 大家过年好&#xff01;新春佳节&#xff0c;在这个充满喜悦的日子里&#xff0c;愿新年的钟声带给你一份希望和期待&#xff0c;我相信&#xff0c;时空的距离不能阻隔你我&#xff0c;我的祝…
阅读更多...
Solidity 中的数学（第 5 部分：指数和对数

Solidity 中的数学（第 5 部分：指数和对数

本文是关于在 Solidity 中进行数学运算的系列文章中的第五篇。这次的主题是&#xff1a;指数和对数 介绍 几个世纪以来&#xff0c;对数被用来简化计算。在电子计算器广泛普及之前&#xff0c;计算尺、基于对数的机械计算器是工程师职业的标志。 对数函数连同指数函数&#x…
阅读更多...
【matplotlib】21.多图合并【python3、numpy、pandas、matplotlib完结】

【matplotlib】21.多图合并【python3、numpy、pandas、matplotlib完结】

#【matplotlib】21.多图合并 2023.1.20 python3、numpy、pandas、matplotlib完结 新年快乐&#xff01;&#xff01; 21.1 多合一显示 21.1.1 均匀分布 方法很简单 就是一张图 分几块 第一张占几块 从哪开始&#xff1b;第二张… plt.subplot() # 打开一个窗口 import ma…
阅读更多...
Redis数据类型简介

Redis数据类型简介

目录 1、字符串(Strings) 1.1、底层实现 1.2、基本命令 1.3、应用场景 2、列表(Lists) 2.1、底层实现 2.2、基本命令 2.3、应用场景 3、集合(Sets) 3.1、底层实现 3.2、基本命令 3.3、应用场景 4、哈希(Hashes) 4.1、底层实现 4.2、基本命令 4.3、应用场景 5、…
阅读更多...
Caché数据库简要记录

Caché数据库简要记录

前一阵子&#xff0c;实施的小伙伴找过来问我用过 Cach 数据库吗&#xff1f;我当时有点懵&#xff1f;难道是 redis、memcached 之流&#xff1f;后来我特意去搜索了一下&#xff0c;还真是有一款数据库叫做 Cach Database。 这里做一下简单的记录吧&#xff0c;Cach 在医疗系…
阅读更多...
Mine Goose Duck 0.1版本发布

Mine Goose Duck 0.1版本发布

我本次制作了一款MC版的Goose Goose Duck模组&#xff0c;游戏版本是Forge 1.19.2。 1.身份物品 熟悉鹅鸭杀的朋友都知道游戏中含有许多的身份&#xff0c;有好人、坏人、中立三个阵营&#xff0c;本次我加入了原作中的一些基本角色&#xff1a; 1.警长 你可以杀死怪物但错…
阅读更多...
DFS（三）电话号码的字母组合

DFS（三）电话号码的字母组合

数组版本 哈希版本&#xff1a; 一、17. 电话号码的字母组合 给定一个仅包含数字 2-9 的字符串&#xff0c;返回所有它能表示的字母组合。答案可以按 任意顺序 返回。 给出数字到字母的映射如下&#xff08;与电话按键相同&#xff09;。注意 1 不对应任何字母。 示例 1&#x…
阅读更多...
Elasticsearch7.8.0版本高级查询——范围查询文档

Elasticsearch7.8.0版本高级查询——范围查询文档

目录一、初始化文档数据二、范围查询文档2.1、概述2.2、示例一、初始化文档数据 在 Postman 中&#xff0c;向 ES 服务器发 POST 请求 &#xff1a;http://localhost:9200/user/_doc/1&#xff0c;请求体内容为&#xff1a; {"name":"张三","age"…
阅读更多...
Git的安装与使用

Git的安装与使用

目录 一、简介 1. Git 是什么&#xff1f; 2. 集中式和分布式 二、Git 环境搭建 1. Linux 下安装 2. Windows 下安装 三、创建版本库 四、把文件添加到版本库 1. 添加并提交 2. 仓库状态 3. 版本回退 &#xff08;1&#xff09;查看提交日志 &#xff08;2&#xff0…
阅读更多...
量化交易-因子有效性分析

量化交易-因子有效性分析

量化交易-因子有效性分析一、 因子的 IC 分析2. 信息系数3. 举例4. 因子处理4.1 去极值4.2 标准化4.3 市值中性化一、 因子的 IC 分析 判断因子与收益的相关性强度 分析结果 因子平均收益IC meanIC stdIC > 0.02&#xff1a;IC大约0.02的比例&#xff0c;越大越严格IR&…
阅读更多...
leetcode刷题记录总结-1. 数组

leetcode刷题记录总结-1. 数组

文章目录一、二分查找[704. 二分查找](https://leetcode.cn/problems/binary-search/)题解小结[35. 搜索插入位置](https://leetcode.cn/problems/search-insert-position/)题解1&#xff1a;暴力解法题解2&#xff1a;二分法[34. 在排序数组中查找元素的第一个和最后一个位置]…
阅读更多...
Day865.基础架构 -MySQL实战

Day865.基础架构 -MySQL实战

基础架构&#xff1a;一条SQL查询语句是如何执行的 Hi&#xff0c;我是阿昌&#xff0c;今天学习记录的关于基础架构&#xff1a;一条SQL查询语句是如何执行的的内容。 经常说&#xff0c;看一个事儿千万不要直接陷入细节里&#xff0c;应该先鸟瞰其全貌&#xff0c;这样能够…
阅读更多...
01-使用Camera Raw滤镜调色

01-使用Camera Raw滤镜调色

1.需求展示 点击下载图片素材 原图 调色后, 具有电影感 2.操作步骤 1.打开原图 1.我使用的是ps2018, 打开原图, 图层名字可以自定义 2.拷贝底片建立一个新图层 养成好习惯, 每种操作都建立新图层来进行, 这样如果修坏了, 直接把该图层删除就行了, 还原图片比较快捷 3…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023