文章目录

一、二分查找
- [704. 二分查找](https://leetcode.cn/problems/binary-search/)
- - 题解
  - - 小结
- [35. 搜索插入位置](https://leetcode.cn/problems/search-insert-position/)
- - 题解1：暴力解法
  - 题解2：二分法
- [34. 在排序数组中查找元素的第一个和最后一个位置](https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/)
- - 题解1: 暴力解法
  - 题解2：二分解法
- [69.x 的平方根](https://leetcode.cn/problems/sqrtx/)
- - 题解1：暴力
  - 题解2：二分法
- 367.有效的完全平方数
- - 题解
二、过滤(删除）保序
- [27. 移除元素](https://leetcode.cn/problems/remove-element/)
- - 题解1：暴力
  - 题解2：单路快慢指针法
  - 题解3：双路指针法
- [977. 有序数组的平方](https://leetcode.cn/problems/squares-of-a-sorted-array/description/)
- - 题解1：暴力
  - 题解2：双指针
- 26.删除排序数组中的重复项
- - 题解
- 283.移动零
- 844.比较含退格的字符串
- - 题解1：重构字符串
  - - `s = String.valueOf(char[] sc)`
    - 或者用`StringBuilder`进行拼凑
  - 题解2：双指针
三、子数组（滑动窗口）
- 209.长度最小的子数组
- - 题解1：暴力
  - 题解2：滑动窗口
- 904.水果成篮
- - 题解
- [76.最小覆盖子串(opens new window)](https://leetcode.cn/problems/minimum-window-substring/)
- - 题解
  - - 优化：
四、拟合（螺旋数组）
- [54. 螺旋矩阵 I](https://leetcode.cn/problems/spiral-matrix/description/)
- - 题解1：方向数组（O(n)空间)
  - 题解2：按层遍历（O(1)空间）
- [59. 螺旋矩阵 II](https://leetcode.cn/problems/spiral-matrix-ii/description/)
- - 题解1：方向数组（O(1)空间)
  - 题解2：按层遍历（O(1)空间）
  - - 小技巧-只适合n*n矩阵

一、二分查找

704. 二分查找

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例 2:

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

提示：

你可以假设 nums 中的所有元素是不重复的。
n 将在 [1, 10000]之间。
nums 的每个元素都将在 [-9999, 9999]之间。

题解

注意

注意边界，while(left <= right)相等时循环继续-防止数组只有一共数，且等于target

class Solution {
    public int search(int[] nums, int target) {
        int n = nums.length;
        int left = 0, right = n - 1;
        while(left <= right) { // 注意边界，相等时循环继续-防止数组只有一共数，且等于target
            int mid = left + (right - left) / 2;
            if(nums[mid] == target) return mid;
            else if(nums[mid] < target) left = mid + 1;
            else right = mid - 1;
        }
        return -1;
    }
}

小结

大家写二分法经常写乱，主要是因为对区间的定义没有想清楚，区间的定义就是不变量。要在二分查找的过程中，保持不变量，就是在while寻找中每一次边界的处理都要坚持根据区间的定义来操作，这就是循环不变量规则。

写二分法，区间的定义一般为两种，左闭右闭即[left, right]，或者左闭右开即[left, right)。

下面我用这两种区间的定义分别讲解两种不同的二分写法。

二分法第一种写法

第一种写法，我们定义 target 是在一个在左闭右闭的区间里，也就是[left, right] （这个很重要非常重要）。

区间的定义这就决定了二分法的代码应该如何写，因为定义target在[left, right]区间，所以有如下两点：

while (left <= right) 要使用 <= ，因为left == right是有意义的，所以使用 <=
if (nums[middle] > target) right 要赋值为 middle - 1，因为当前这个nums[middle]一定不是target，那么接下来要查找的左区间结束下标位置就是 middle - 1

35. 搜索插入位置

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

示例 1:

输入: nums = [1,3,5,6], target = 5
输出: 2

示例 2:

输入: nums = [1,3,5,6], target = 2
输出: 1

示例 3:

输入: nums = [1,3,5,6], target = 7
输出: 4

提示:

1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 为 无重复元素 的升序排列数组
-104 <= target <= 104

题解1：暴力解法

这道题目不难，但是为什么通过率相对来说并不高呢，我理解是大家对边界处理的判断有所失误导致的。
这道题目，要在数组中插入目标值，无非是这四种情况。
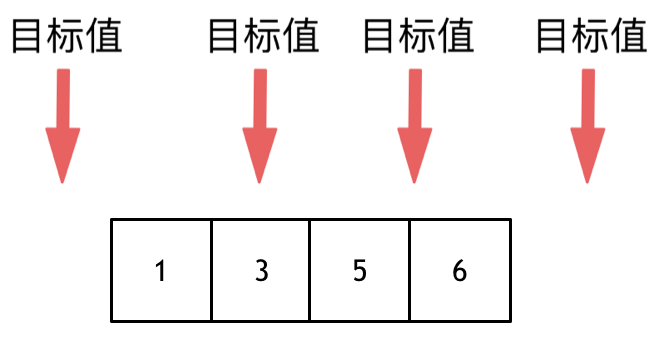
- 目标值在数组所有元素之前
- 目标值等于数组中某一个元素
- 目标值插入数组中的位置
- 目标值在数组所有元素之后

class Solution {
    // 方法1：暴力搜索
    public int searchInsert(int[] nums, int target) {
        int n = nums.length;
        int i = 0;
        if(nums[i] > target) return i; // 比数组所有元素都小-所有元素之前
        for(; i < n; i ++) {
            if(nums[i] == target) return i;// 等于
            else if(i < n - 1 && nums[i] < target && nums[i + 1] > target) return i + 1;// 注意边界              
        }
        return i; // 比数组所有元素都大-所有元素之后
    }
}

题解2：二分法

二分法，对于剩下三种情况，可以用找到的right求出

// 处理剩下三种情况；
// 2.所有元素前面，right一直走到-1
// 3.插入元素中间，即在[right, left]中插入，位置为right + 1
// 4.所有元素后面，right没有边，还是n-1,要在右边插入一个

class Solution {
    // 二分法，对于剩下三种情况，可以用找到的right求出
    public int searchInsert(int[] nums, int target) {
        int n = nums.length;
        int left = 0, right = n - 1;
        while(left <= right) {
            int mid = left + (right - left) / 2;
            if(nums[mid] == target) return mid; // 1.等于target
            else if(nums[mid] > target) right = mid - 1;
            else left = mid + 1;
        }
        // 处理剩下三种情况；
        // 2.所有元素前面，right一直走到-1
        // 3.插入元素中间，即在[right, left]中插入，位置为right + 1
        // 4.所有元素后面，right没有变，还是n-1,要在右边插入一个
        return right + 1;
    }
}

34. 在排序数组中查找元素的第一个和最后一个位置

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

示例 2：

输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

示例 3：

输入：nums = [], target = 0
输出：[-1,-1]

提示：

0 <= nums.length <= 105
-10^9 <= nums[i] <= 10^9
nums 是一个非递减数组
-10^9 <= target <= 10^9

题解1: 暴力解法

class Solution {
    // 1.暴力解法
    public int[] searchRange(int[] nums, int target) {
        int start = -1, last = -1;
        for(int i = 0; i < nums.length; i ++) {
            if(nums[i] == target) {
                if(start == -1) start = i;
                last = i;
            }
        }
        return new int[]{start, last};
    }
}

题解2：二分解法

四种情况：
- 1.target在所有元素前面-找不到目标值
- 2.target在所有元素后面-找不到目标值
- 3.target在数组范围内，但与元素均不等
- 4.target在数组范围内，能找到相等元素，且可能不止一个
两个边界
- 左边界：第一次相等的元素的左边界，[leftBordre, target, ...],即不包括target
- 右边界：最后一次相等的元素的右边界，[leftBorder, target...target, rightBorder...],不包括target

class Solution {
    // 1.二分查找
    int n;
    public int[] searchRange(int[] nums, int target) {
        n = nums.length;
        int leftBorder = findLeftBorder(nums, target);
        int rightBorder = findRightBorder(nums, target);
        // 情况4：能找到目标元素
        if(rightBorder - leftBorder > 1) return new int[]{leftBorder + 1, rightBorder - 1};
        // 找不到目标元素的情况1，2，3
        return new int[]{-1, -1};
    }

    // 找第一次出现相等元素的左边界-不包括target
    private int findLeftBorder(int[] nums, int target) {
        int left = 0, right = n - 1;
        // int leftBorder = -1;
        while(left <= right) {
            int mid = left + (right - left) / 2;
            if(nums[mid] > target) right = mid -1; // mid右边排除            
            else if(nums[mid] == target) {// 有可能不是第一次相等，mid右边排除，往左继续找
                right = mid -1;
                // leftBorder = right; //更新左边界
            } else left = mid + 1;
        }
        return right; // -1, n-1，right<left，target下标-1：分别对应四种情况
    }

     // 找最后次出现相等元素的左边界-不包括target
    private int findRightBorder(int[] nums, int target) {
        int left = 0, right = n - 1;
        while(left <= right) {
            int mid = left + (right - left) / 2;
            if(nums[mid] > target) right = mid -1; // mid右边排除            
            else if(nums[mid] == target) {// 有可能不是最后一次相等，mid左边排除，往右继续找
                left = mid + 1;
            } else left = mid + 1;
        }
        return left; // 0, n+1，right<left，target下标+1：分别对应四种情况
    }
}

69.x 的平方根

给你一个非负整数 x ，计算并返回 x 的 算术平方根 。

由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去。

**注意：**不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。

示例 1：

输入：x = 4
输出：2

示例 2：

输入：x = 8
输出：2
解释：8 的算术平方根是 2.82842..., 由于返回类型是整数，小数部分将被舍去。

提示：

0 <= x <= 2^31 - 1

题解1：暴力

**注意：**要防止数据越界，将乘法改成除法

class Solution {
    public int mySqrt(int x) {
        int num = 1;
        while(num <= x / num) { // 要防止数据越界，num * num <= x
            num ++;
            if(num  > x / num) {
                return --num;
            }
        }
        return 0;
    }
}

题解2：二分法

class Solution {
    public int mySqrt(int x) {
        int left = 1, right = x;
        while(left <= right) {
            int mid = left + (right - left) / 2;
            if(mid == x / mid) return mid;
            else if(mid < x / mid) left = mid + 1;
            else right = mid - 1;
        }
        return right;
    }
}

367.有效的完全平方数

给定一个 正整数 num ，编写一个函数，如果 num 是一个完全平方数，则返回 true ，否则返回 false 。

进阶：不要 使用任何内置的库函数，如 sqrt 。

示例 1：

输入：num = 16
输出：true

示例 2：

输入：num = 14
输出：false

提示：

1 <= num <= 2^31 - 1

题解

注意

为了得到精确的值，将比较结果设定为浮点型
- 例如num = 5, mid = 2， 2 == 5 / 2,这样，会找出错误的答案

class Solution {
    public boolean isPerfectSquare(int num) {
        int left = 1, rigth = num;
        while(left <= rigth) {
            int mid = left + (rigth - left) / 2;
            if(mid == num*1.0 / mid) { // 注意，为了得到精确的值，将结果设定为浮点型
                System.out.println(mid);
                return true;
            }
            else if(mid < num / mid) left = mid + 1;
            else rigth = mid - 1;
        }
        return false;
    }
}

二、过滤(删除）保序

27. 移除元素

给你一个数组 nums 和一个值 val，你需要原地移除所有数值等于 val 的元素，并返回移除后数组的新长度。

不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地修改输入数组。

元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

说明:

为什么返回数值是整数，但输出的答案是数组呢?

请注意，输入数组是以**「引用」**方式传递的，这意味着在函数里修改输入数组对于调用者是可见的。

你可以想象内部操作如下:

// nums 是以“引用”方式传递的。也就是说，不对实参作任何拷贝
int len = removeElement(nums, val);

// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。
for (int i = 0; i < len; i++) {
    print(nums[i]);
}

示例 1：

输入：nums = [3,2,2,3], val = 3
输出：2, nums = [2,2]
解释：函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如，函数返回的新长度为 2 ，而 nums = [2,2,3,3] 或 nums = [2,2,0,0]，也会被视作正确答案。

示例 2：

输入：nums = [0,1,2,2,3,0,4,2], val = 2
输出：5, nums = [0,1,4,0,3]
解释：函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。

提示：

0 <= nums.length <= 100
0 <= nums[i] <= 50
0 <= val <= 100

题解1：暴力

按照数组正常的删除逻辑，删除指定元素，后面的所有元素均向前移动覆盖
用时间换空间

注意

为了删除重复等于val的元素，
- 使用while时要注意，删除最后一个元素时或数组中都是要删除的元素，无法移动覆盖，会一直死循环

class Solution {
    public int removeElement(int[] nums, int val) {
        int size = nums.length; // 实践的删除，删除后，数组容量也变化
        if(size == 0) return 0;
        for(int i = 0; i < size; i ++) { 
            // 为了删除重复等于val的元素，
            // 使用while时要注意，删除最后一个元素时或数组中都是要删除的元素，无法移动覆盖，会一直死循环
            if(nums[i] == val) { // 要删除的元素，后面所有元素均向前移动一位
                for(int j = i + 1; j < size; j ++) {
                    nums[j - 1] = nums[j];
                }
                i --;       // i的值被覆盖了，因此i要向前移动一步，继续判断被覆盖的值
                size --;    // 维护数组容量
            }
        }
        return size;
    }
}

题解2：单路快慢指针法

单路指针，就是过滤保序模型，用快指针进行过滤，过滤后的元素，用慢指针保序
- 类似题目：26. 删除有序数组中的重复项

// 注意，原地空间，不代表只能在移动原有数组元素，只是移动覆盖，会有很多冗余操作，需要消耗额外的性能
// 原地空间，可以增加几个变量，只不过还是使用原有数组的空间而已

class Solution {
    // 双指针，一个指针保序（有效元素在前面），一个指针过滤（寻找有效元素）
    public int removeElement(int[] nums, int val) {
        int slow = 0, fast = 0;
        for(;fast < nums.length; fast ++) {
            if(nums[fast] != val) {
                nums[slow ++] = nums[fast];
            }
        }
        return slow;
    }
}

题解3：双路指针法

双指针从两边向中间递进，可以减少指针遍历的次数
双指针分别维护相反的目标，然后进行交换，截取想要的部分

class Solution {
    public int removeElement(int[] nums, int val) {
       int n = nums.length;
       // left查找等于val,right查找不等val，不满足时阻塞，交换
       // 最终，left维护不等val的右边界
       int left = 0, right = n - 1; 
       while(left <= right) { // 左闭右闭，相等时有效，要进行判断
            // 1. left维护不等val,查找等于val的位置-停止，等待处理
            while(left <= right && nums[left] != val) left ++;
            // 2. right维护等于val的位置，遇到不等时，停止，等待处理
            while(left <= right && nums[right] == val) right --; // 相当于也过滤掉一部分等于val的值
            // 3. 交换，保证left指向的一定是不等val的位置
            if(left < right) nums[left ++] = nums[right --]; // 交换处理后，继续走下去
       }
       return left;
    }
}

977. 有序数组的平方

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

示例 1：

输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]

示例 2：

输入：nums = [-7,-3,2,3,11]
输出：[4,9,9,49,121]

提示：

1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 已按 非递减顺序 排序

进阶：

请你设计时间复杂度为 O(n) 的算法解决本问题

题解1：暴力

class Solution {
    public int[] sortedSquares(int[] nums) {
        int n = nums.length;
        int[] arr = new int[n];
        for(int i = 0; i < n; i ++) arr[i] = nums[i] * nums[i];
        Arrays.sort(arr);
        return arr;
    }
}

题解2：双指针

注意

要新开数组，免得污染原数组

class Solution {
    // 双指针双路法，分别指向两端（平方后两端最大，中间小）
    // 定义一个指针保序，上面两个指针用来过滤，找最大值
    public int[] sortedSquares(int[] nums) {
        int n = nums.length;
        int l = 0, r = n - 1, i = n - 1;
        // 要新开数组，免得污染原数组
        int[] res = new int[n];
        while(l <= r) {
            if(nums[l] * nums[l] < nums[r] * nums[r]) {
                res[i --] = nums[r] * nums[r];
                r --;
            } else {
                res[i --] = nums[l] * nums[l];
                l ++;
            }
        }
        return res;
    }
}

26.删除排序数组中的重复项

给你一个 升序排列 的数组 nums ，请你** 原地** 删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度。元素的 相对顺序 应该保持一致。

由于在某些语言中不能改变数组的长度，所以必须将结果放在数组nums的第一部分。更规范地说，如果在删除重复项之后有 k 个元素，那么 nums 的前 k 个元素应该保存最终结果。

将最终结果插入 nums 的前 k 个位置后返回 k 。

不要使用额外的空间，你必须在 原地修改输入数组 并在使用 O(1) 额外空间的条件下完成。

判题标准:

系统会用下面的代码来测试你的题解:

int[] nums = [...]; // 输入数组
int[] expectedNums = [...]; // 长度正确的期望答案

int k = removeDuplicates(nums); // 调用

assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
    assert nums[i] == expectedNums[i];
}

如果所有断言都通过，那么您的题解将被通过。

示例 1：

输入：nums = [1,1,2]
输出：2, nums = [1,2,_]
解释：函数应该返回新的长度 2 ，并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。

示例 2：

输入：nums = [0,0,1,1,1,2,2,3,3,4]
输出：5, nums = [0,1,2,3,4]
解释：函数应该返回新的长度 5 ， 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。

提示：

1 <= nums.length <= 3 * 104
-104 <= nums[i] <= 104
nums 已按升序排列

题解

class Solution {
    public int removeDuplicates(int[] nums) {
        int cnt = 0; // 保序
        for(int i = 0; i < nums.length; i ++) {
            if(i == 0 || nums[i] != nums[i - 1]) { // 过滤
                nums[cnt ++] = nums[i];
            }
        }
        return cnt;
    }
}

283.移动零

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

请注意 ，必须在不复制数组的情况下原地对数组进行操作。

示例 1:

输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]

示例 2:

输入: nums = [0]
输出: [0]

提示:

1 <= nums.length <= 104
-231 <= nums[i] <= 231 - 1

**进阶：**你能尽量减少完成的操作次数吗？

class Solution {
    public void moveZeroes(int[] nums) {
        int cnt = 0; // 保序
        for(int i = 0; i < nums.length; i ++) {
            if(nums[i] != 0) { // 过滤
                nums[cnt ++] = nums[i];
            }
        }
        // 注意，最后的数要用0来填充
        for(int i = cnt; i < nums.length; i ++) {
            nums[cnt ++] = 0;
        }
    }
}

844.比较含退格的字符串

给定 s 和 t 两个字符串，当它们分别被输入到空白的文本编辑器后，如果两者相等，返回 true 。# 代表退格字符。

**注意：**如果对空文本输入退格字符，文本继续为空。

示例 1：

输入：s = "ab#c", t = "ad#c"
输出：true
解释：s 和 t 都会变成 "ac"。

示例 2：

输入：s = "ab##", t = "c#d#"
输出：true
解释：s 和 t 都会变成 ""。

示例 3：

输入：s = "a#c", t = "b"
输出：false
解释：s 会变成 "c"，但 t 仍然是 "b"。

提示：

1 <= s.length, t.length <= 200
s 和 t 只含有小写字母以及字符 '#'

进阶：

你可以用 O(n) 的时间复杂度和 O(1) 的空间复杂度解决该问题吗？

题解1：重构字符串

`s = String.valueOf(char[] sc)`

class Solution {
    public boolean backspaceCompare(String s, String t) {
        char[] c1 = s.toCharArray();
        char[] c2 = t.toCharArray();
        Stack<Character> stack = new Stack<>();
        // 1.重构s字符串
        for(char c : c1) {
            if(c != '#') stack.push(c);
            else if(!stack.isEmpty()) stack.pop();           
        }
        char[] sc = new char[stack.size()];
        for(int i = stack.size() - 1; i >= 0; i --) {
            sc[i] = stack.pop();
        }
        s = String.valueOf(sc);
        // 2.重构t字符串
        for(char c : c2) {
            if(c != '#') stack.push(c);
            else if(!stack.isEmpty()) stack.pop();          
        }
        char[] tc = new char[stack.size()];
        for(int i = stack.size() - 1; i >= 0; i --) {
            tc[i] = stack.pop();
        }
        t = String.valueOf(tc);
        return s.equals(t);
    }
}

或者用`StringBuilder`进行拼凑

ret.append(ch)
ret.deleteCharAt(ret.length() - 1)

class Solution {
    public boolean backspaceCompare(String S, String T) {
        return build(S).equals(build(T));
    }

    public String build(String str) {
        StringBuffer ret = new StringBuffer();
        int length = str.length();
        for (int i = 0; i < length; ++i) {
            char ch = str.charAt(i);
            if (ch != '#') {
                ret.append(ch);
            } else {
                if (ret.length() > 0) {
                    ret.deleteCharAt(ret.length() - 1);
                }
            }
        }
        return ret.toString();
    }
}

题解2：双指针

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QYWTVXaP-1674221881684)(assets/image-20221120034623407.png)]

class Solution {
    public boolean backspaceCompare(String S, String T) {
        int i = S.length() - 1, j = T.length() - 1;
        int skipS = 0, skipT = 0;

        while (i >= 0 || j >= 0) {
            // 1.处理s字符串-退格符对普通字符的消除工作
            while (i >= 0) {
                if (S.charAt(i --) == '#') { // 记录普通字符前退格符数量
                    skipS++;
                } else if (skipS > 0) {   // 如果为普通字符，查看前面退格符数量
                    skipS--;
                    i--;
                } else {
                    break;  // 没有空格，不用处理
                }
            }
            // 2.处理t字符-退格符对普通字符的消除工作
            while (j >= 0) {
                if (T.charAt(j) == '#') {
                    skipT++;
                    j--;
                } else if (skipT > 0) {
                    skipT--;
                    j--;
                } else {
                    break;
                }
            }
            // 3.普通字符前面的退格符消除后，找到的有效字符
            if (i >= 0 && j >= 0) { // 两字符串均没有bian'l
                if (S.charAt(i) != T.charAt(j)) {
                    return false;
                }
            } else { // 其中有一个遍历完，另一个却没有，说明字符数量不等，一定不等
                if (i >= 0 || j >= 0) {
                    return false;
                }
            }
            // 4.当前两个字符即没有走完，当前字符也相等，继续判断下一组字符
            i--;
            j--;
        }
        return true;
    }
}

三、子数组（滑动窗口）

209.长度最小的子数组

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例 1：

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：

输入：target = 4, nums = [1,4,4]
输出：1

示例 3：

输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

提示：

1 <= target <= 109
1 <= nums.length <= 105
1 <= nums[i] <= 105

进阶：

如果你已经实现 O(n) 时间复杂度的解法, 请尝试设计一个 O(n log(n)) 时间复杂度的解法。

题解1：暴力

时间超了，本题通过不了

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int n = nums.length;
        int ans = Integer.MAX_VALUE;
        for(int i = 0; i < n; i ++) {
            int sum = 0;
            for(int j = i; j < n; j ++) {
                sum += nums[j]; // 要判断第一个数自身是否为target
                if(sum >= target) {
                    ans = Math.min(ans, j - i + 1);
                    break;
                }
            }
        }
        return ans == Integer.MAX_VALUE ? 0 : ans;
    }
}

题解2：滑动窗口

滑动窗口，就是不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果

主要确定如下三点：

窗口内是什么？
如何移动窗口的起始位置？
如何移动窗口的结束位置？

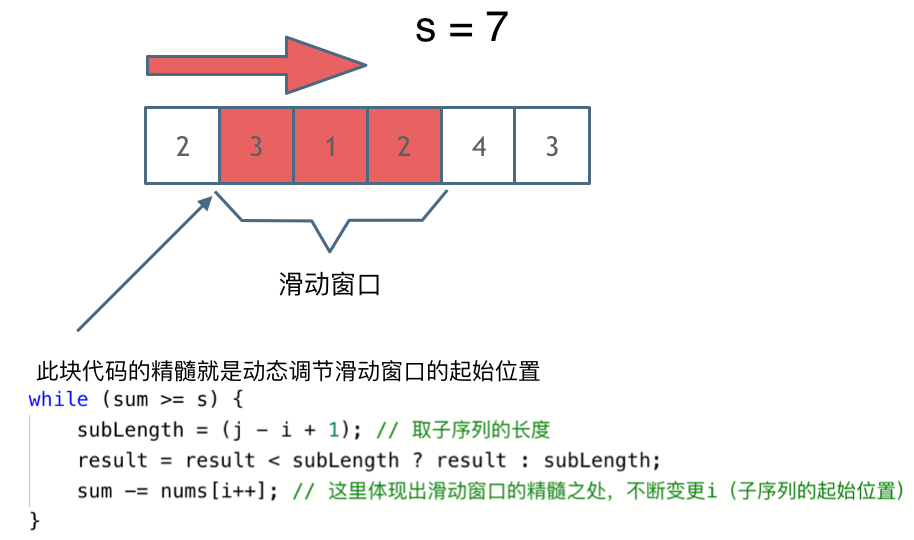
leetcode_209

可以发现滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将O(n^2)暴力解法降为O(n)。

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int n = nums.length;
        int ans = Integer.MAX_VALUE;
        int l = 0;          // 窗口左边界，循环外。每次动态调整
        int sum = 0;  
        for(int r = 0; r < n; r ++) { // 窗口右边界循序遍历           
            sum += nums[r];           // 窗口装子序列和，要保证>=target
            while(sum >= target) { // 保证满足前提下，调整左边界找最小的区间
                ans = Math.min(ans, r - l + 1);
                sum -= nums[l ++];  // 动态调整左边界，缩小窗口
            }
        }
        return ans == Integer.MAX_VALUE ? 0 : ans;
    }
}

904.水果成篮

你正在探访一家农场，农场从左到右种植了一排果树。这些树用一个整数数组 fruits 表示，其中 fruits[i] 是第 i 棵树上的水果种类。

你想要尽可能多地收集水果。然而，农场的主人设定了一些严格的规矩，你必须按照要求采摘水果：

你只有两个篮子，并且每个篮子只能装 单一类型 的水果。每个篮子能够装的水果总量没有限制。
你可以选择任意一棵树开始采摘，你必须从每棵树（包括开始采摘的树）上 恰好摘一个水果 。采摘的水果应当符合篮子中的水果类型。每采摘一次，你将会向右移动到下一棵树，并继续采摘。
一旦你走到某棵树前，但水果不符合篮子的水果类型，那么就必须停止采摘。

给你一个整数数组 fruits ，返回你可以收集的水果的最大数目。

示例 1：

输入：fruits = [1,2,1]
输出：3
解释：可以采摘全部 3 棵树。

示例 2：

输入：fruits = [0,1,2,2]
输出：3
解释：可以采摘 [1,2,2] 这三棵树。
如果从第一棵树开始采摘，则只能采摘 [0,1] 这两棵树。

示例 3：

输入：fruits = [1,2,3,2,2]
输出：4
解释：可以采摘 [2,3,2,2] 这四棵树。
如果从第一棵树开始采摘，则只能采摘 [1,2] 这两棵树。

示例 4：

输入：fruits = [3,3,3,1,2,1,1,2,3,3,4]
输出：5
解释：可以采摘 [1,2,1,1,2] 这五棵树。

提示：

1 <= fruits.length <= 105
0 <= fruits[i] < fruits.length

题解

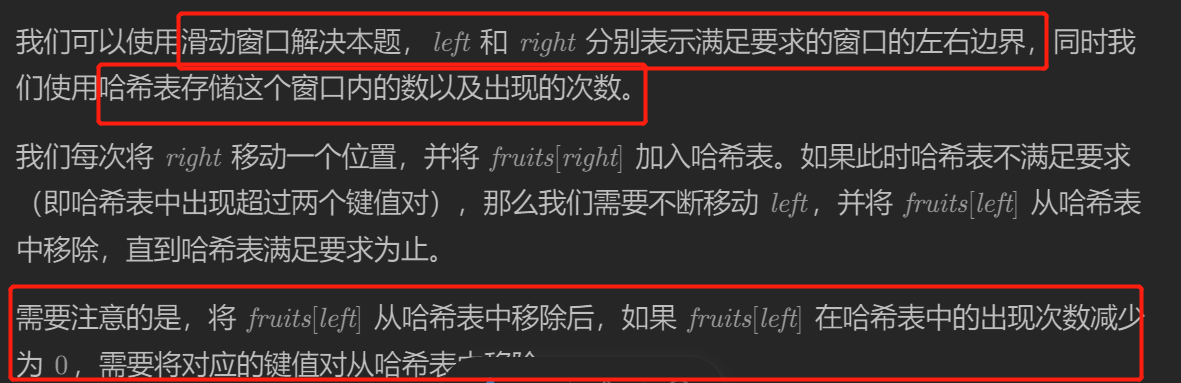
在这里插入图片描述

与之前的滑动窗口逻辑不同
- 长度最小的子数组，初始是不满足的，移动右边界，使之满足，在满足的前提下，调整左边界找最优解
  - 因此每次调整前要更新答案
- 本题是初始满足，移动有边界会可能变得不满足，需要调整左边界使之先满足，调整后再更新答案
  - 因此每次调整后再更新答案

class Solution {
    // 题意：保证三点：
    // 1.只能包含两种数(用哈希key<=2) 2.区间连续（可以使用滑动窗口） 3.区间最大
    public int totalFruit(int[] fruits) {
        int n = fruits.length;
        int l = 0; // 窗口左边界，当不满足时，缩小窗口以满足条件
        int r = 0; // 窗口右边界，当满足时，不断向右扩展，找最大窗口
        int ans = Integer.MIN_VALUE;
        HashMap<Integer, Integer> hash = new HashMap<>(); // 记录
        for(; r < n; r ++) {
            // 先将右边界放入哈希表，形成窗口，进行判断
            hash.put(fruits[r], hash.getOrDefault(fruits[r], 0) + 1);
            // 判断窗口是否满足，如果不满足，进行动态调整左边界
            while(hash.size() > 2) { // 因为先满足，移动右后会变不满足，所以移动左再次满足
                int key = fruits[l ++];//要处理的边界，先值减一再看是是否剔除
                hash.put(key, hash.get(key) - 1);
                if(hash.get(key) == 0) hash.remove(key);
            }
            // 窗口满足后，更新答案
            ans = Math.max(ans, r - l + 1);
        }
        return ans;
    }
}

76.最小覆盖子串(opens new window)

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 "" 。

注意：

对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
如果 s 中存在这样的子串，我们保证它是唯一的答案。

示例 1：

输入：s = "ADOBECODEBANC", t = "ABC"
输出："BANC"

示例 2：

输入：s = "a", t = "a"
输出："a"

示例 3:

输入: s = "a", t = "aa"
输出: ""
解释: t 中两个字符 'a' 均应包含在 s 的子串中，
因此没有符合条件的子字符串，返回空字符串。

提示：

1 <= s.length, t.length <= 105
s 和 t 由英文字母组成

**进阶：**你能设计一个在 o(n) 时间内解决此问题的算法吗？

题解

寻找子串问题，且是线性的，可用滑动窗口解决
滑动窗口的精髓是两个指针，每次一个指针移动，一个指针静止
- 右边界指针用来扩展窗口，寻找窗口满足的条件，满足时，停下找左边界
- 左边界指针用来缩小窗口，寻找满足条件的最优解，不满足时，停下找右边界
如何判断窗口满足：对于字符串或有重复元素的例子，可以使用哈希表储存判断
- 一个哈希表th记录t中所有字符以及他们的个数
- 一个哈希表sh记录动态维护窗口中的字符以及他们的个数
- 比较两个哈希表，sh中包含th中的每个key，并且sh字符个数小于th对于key的字符个数，满足

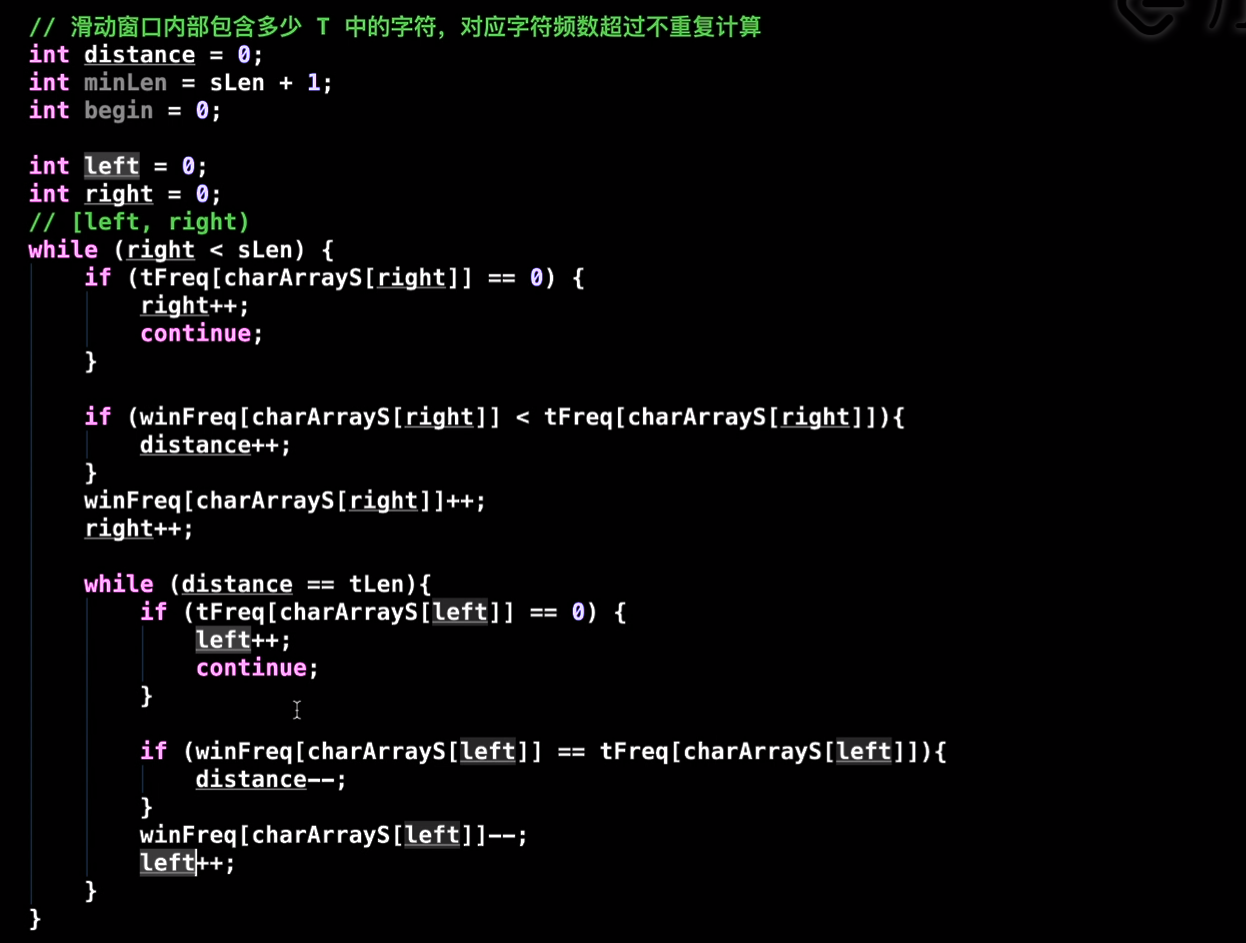
class Solution {
    HashMap<Character, Integer> tmap = new HashMap<>();
    HashMap<Character, Integer> smap = new HashMap<>();
    public String minWindow(String s, String t) {
        int n = s.length();
        char[] tArr = t.toCharArray();
        char[] sArr = s.toCharArray(); // 转为字符数组提高性能
        for(char c : tArr) {
            tmap.put(c, tmap.getOrDefault(c, 0) + 1);
        }
        int left = 0;  // 窗口左边界
        int len = n + 1, start = -1;//要截取的起始位置和长度
        for(int right = 0; right < n; right ++) { // 窗口右边界扩展
            char rightChar = sArr[right]; 
            // 非t字符，无需放入smap，继续右边扩展
            if(tmap.containsKey(rightChar)) {
                smap.put(rightChar,smap.getOrDefault(rightChar, 0) + 1);
            }
            // 扩展后，判断是否满足，如果满足，更新答案，缩小窗口找最优解
            while(check()) {
                // 先更新答案，再缩小窗口,更新smap
                if(right - left + 1 < len) {
                    len = right - left + 1;
                    start = left;
                }
                char leftChar = sArr[left ++];
                if(tmap.containsKey(leftChar)) {
                    // val减去后，=0时可以不用删除key,因为比较的是val
                    smap.put(leftChar, smap.getOrDefault(leftChar, 0) - 1);
                }
            }
        }
        return len == n + 1 ? "" : s.substring(start, start + len);
    }

    private boolean check() {
        for(Character key : tmap.keySet()) {
            if(smap.getOrDefault(key, 0) < tmap.get(key)) return false;
        }
        return true;
    }
}

优化：

用distance变量记录t中所有字符累加的值，如果相等，就满足，省去哈希判断的复杂度

在这里插入图片描述

四、拟合（螺旋数组）

54. 螺旋矩阵 I

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：

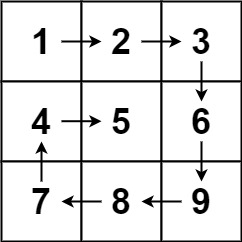
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-xD6AH8ac-1674221887732)(null)]

输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 10
-100 <= matrix[i][j] <= 100

题解1：方向数组（O(n)空间)

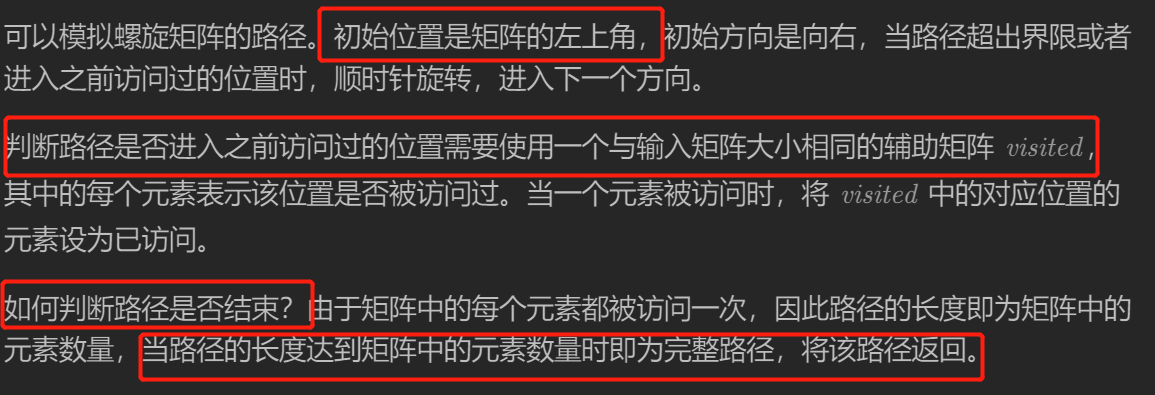
在这里插入图片描述

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> list = new ArrayList<>();
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return list;
        }
        int rows = matrix.length;    // 行数
        int cols = matrix[0].length; // 列数
        int tol = rows * cols;       // 数的总个数，要遍历处理的边界
        int row = 0, col = 0;        // 每次处理的行、列
        int[] dx = new int[]{0, 1, 0, -1}; // 顺时针：北、东、南、西   
        int[] dy = new int[]{1, 0, -1, 0}; // 左上角为坐标原点
        int dir = 0;        // 方向因子(dir + 1) % 4,为顺时针选择
        boolean[][] visited = new boolean[rows][cols];//是否重复访问

        for(int i = 0; i < tol; i ++) {
            // 1.先记录访问的点
            list.add(matrix[row][col]);
            // 2.标记已经访问
            visited[row][col] = true;
            // 3.通过方向数组，查找下个访问的位置，判断是否需要旋转
            int nextRow = row + dx[dir];
            int nextCol = col + dy[dir];
            if(nextRow < 0 || nextRow >= rows || nextCol < 0 || nextCol >= cols || visited[nextRow][nextCol]) dir = (dir + 1) % 4;
            // 4.用最新的方向因子更新下个访问的位置
            row += dx[dir];
            col += dy[dir];
        }
        return list;
    }
}

题解2：按层遍历（O(1)空间）

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> list = new ArrayList<>();
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return list;
        }
        int rows = matrix.length;    // 行数
        int cols = matrix[0].length; // 列数
        int left = 0, right = cols - 1, top = 0, bot = rows - 1; //边界
        while(left <= right && top <= bot) {
            // 1.顶层，从左往右，左闭右闭-这样，最后一个中间的元素也可以访问到
            for(int i = left; i <= right; i ++) {
                list.add(matrix[top][i]);
            }
            // 2.右层，从上往下，左闭右闭。最后一列也能访问到
            for(int i = top + 1; i <= bot; i ++) {
                list.add(matrix[i][right]);
            }
            if(left < right && top < bot) { //走到最后一行或最后一列时，跳出
                // 3.下层，从右往左，左闭右开
                for(int i = right - 1; i > left; i --) {
                    list.add(matrix[bot][i]);
                }
                // 4.左层，从下往上，左闭右开
                for(int i = bot; i > top; i --) {// 不能与上面数撞上
                    list.add(matrix[i][left]);
                }
            }
            left++; right--; top++; bot--;
        }
        return list;
    }
}

59. 螺旋矩阵 II

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1：

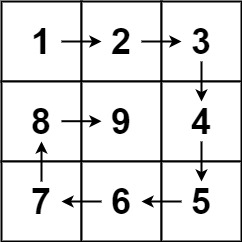
输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

示例 2：

输入：n = 1
输出：[[1]]

提示：

1 <= n <= 20

题解1：方向数组（O(1)空间)

与上题不同，因为数组初始都为0，添加后的数组元素都大于0，因此，无需开额外空间判断是否访问过了

class Solution {
    public int[][] generateMatrix(int n) {
        int[][] res = new int[n][n];
        int curNum = 1, maxNum = n * n;
        int[] dx = new int[]{0, 1, 0, -1};
        int[] dy = new int[]{1, 0, -1, 0};
        int dir = 0;
        int row = 0, col = 0;
        while(curNum <= maxNum) {
            // 1.先访问矩阵位置，更新答案
            res[row][col] = curNum++;
            // 2.通过方向数组，查找下个访问的位置，判断是否需要旋转
            int nextRow = row + dx[dir];
            int nextCol = col + dy[dir];
            if(nextRow < 0 || nextRow >= n || nextCol < 0 
                || nextCol >= n || res[nextRow][nextCol] != 0){
                    dir = (dir + 1) % 4;
            }
            // 3. 用最新的方向数组更新下个位置
            row += dx[dir];
            col += dy[dir];
        }
        return res;
    }
}

题解2：按层遍历（O(1)空间）

class Solution {
    public int[][] generateMatrix(int n) {
        int[][] res = new int[n][n];
        int curNum = 1;
        int left = 0, right = n - 1, top = 0, bot = n - 1; //边界
        while(left <= right && top <= bot) {
            // 1.顶层，从左往右，左闭右闭-这样，最后一个中间的元素也可以访问到
            for(int i = left; i <= right; i ++) {
                res[top][i] = curNum++;
            }
            // 2.右层，从上往下，左闭右闭。最后一列也能访问到
            for(int i = top + 1; i <= bot; i ++) {
                res[i][right] = curNum++;
            }
            if(left < right && top < bot) { //走到最后一行或最后一列时，跳出
                // 3.下层，从右往左，左闭右开
                for(int i = right - 1; i > left; i --) {
                    res[bot][i] = curNum++;
                }
                // 4.左层，从下往上，左闭右开
                for(int i = bot; i > top; i --) {// 不能与上面数撞上
                    res[i][left] = curNum++;
                }
            }
            left++; right--; top++; bot--;
        }
        return res;
    }
}

小技巧-只适合n*n矩阵

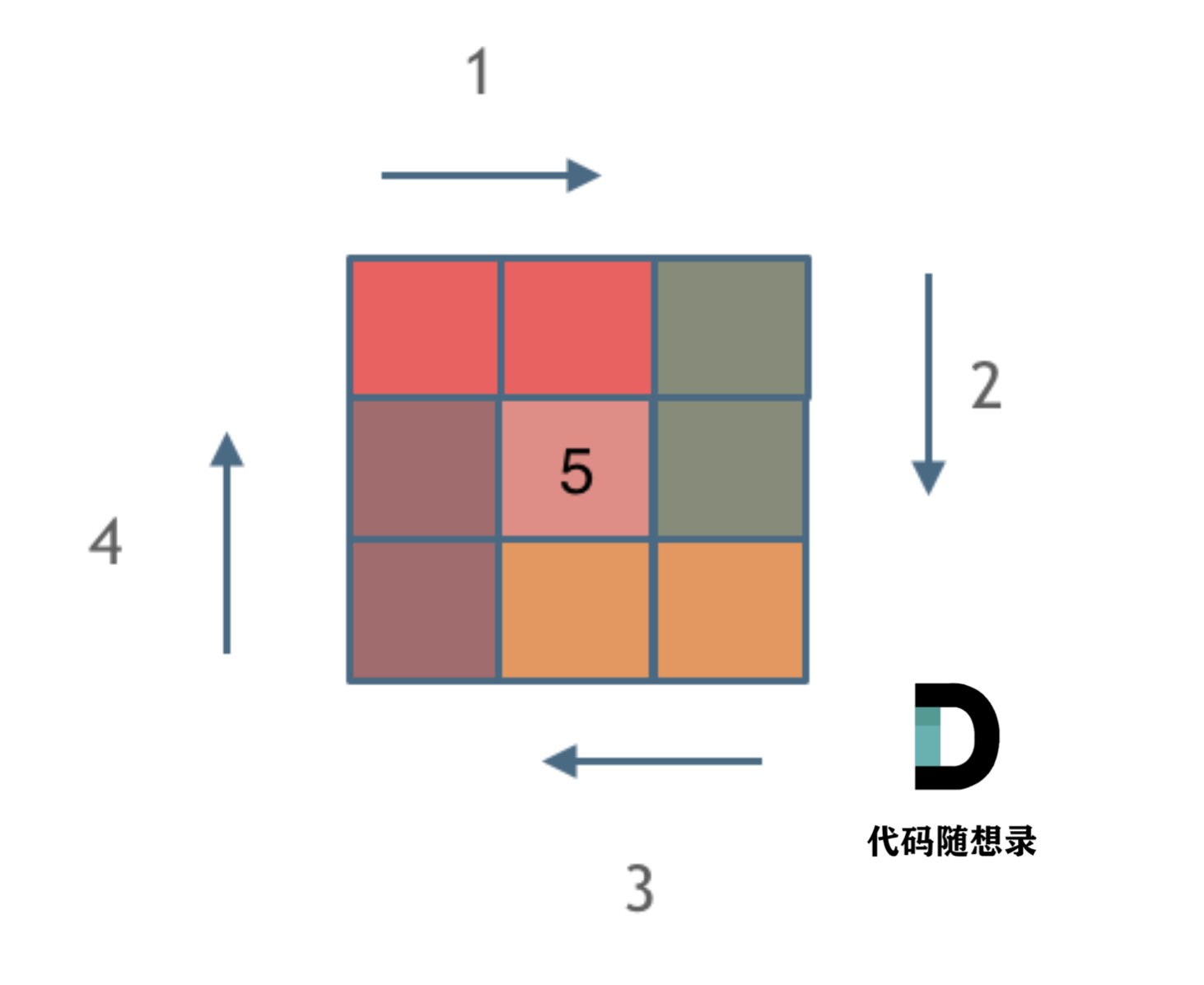
求解本题依然是要坚持循环不变量原则。

模拟顺时针画矩阵的过程:

填充上行从左到右
填充右列从上到下
填充下行从右到左
填充左列从下到上

由外向内一圈一圈这么画下去。

可以发现这里的边界条件非常多，在一个循环中，如此多的边界条件，如果不按照固定规则来遍历，那就是一进循环深似海，从此offer是路人。
这里一圈下来，我们要画每四条边，这四条边怎么画，每画一条边都要坚持一致的左闭右开，或者左开右闭的原则，这样这一圈才能按照统一的规则画下来。

那按照左闭右开的原则，来画一圈：

class Solution {
    public int[][] generateMatrix(int n) {
        int count = 1; // 矩阵中的数，依次往上累加到n*n
        int[][] res = new int[n][n];
        int loop = n / 2; // 循环填入的次数
        int mid = n / 2 ; // n为奇数时，中间数要单独处理(mid, mid)
        int startx = 0, starty = 0; // 行数和列数起始位置，每轮增加
        int offset = 1; // 有边界的偏量，左闭右开，第一次偏1，后面每次+1
        int i, j;   // 循环移动的指针
        while(loop-- > 0) {
            // 1.每轮循环时更新指针指向新的起始位置
            i = startx; j = starty;
            // 2.顶行，（起始）从左往右遍历，左闭右开，不包括最右边界
            for(; j < n - offset; j ++) {
                res[startx][j] = count++;
            }
            // 3.右列，从上往下遍历，左闭右开
            for(; i < n - offset; i ++) {
                res[i][j] = count++;
            }
            // 4.底行，从右往左遍历，左闭右开
            for(; j > starty; j --) {
                res[i][j] = count++;
            }
            // 5.左列，从下往上遍历，左闭右开
            for(; i > startx; i --) {
                res[i][j] = count++;
            }
            // 6.下一轮开始，更新起始位置和偏移量
            startx++; starty++; offset++;
        }
        // 7.注意n为奇数时，需要单独给矩阵最中间位置赋值
        if(n % 2 == 1) res[mid][mid] = count;
        return res;
    }
}