本文是关于在 Solidity 中进行数学运算的系列文章中的第五篇。这次的主题是:指数和对数

介绍
几个世纪以来,对数被用来简化计算。在电子计算器广泛普及之前,计算尺、基于对数的机械计算器是工程师职业的标志。
对数函数连同指数函数(指数函数是对数函数的倒数)允许将乘法转换为加法,更重要的是,可以将求幂转换为乘法。由于以下两个规则,这是可能的:
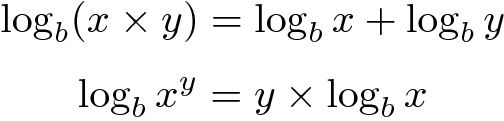
在对这些方程的左右部分取幂后,我们有:
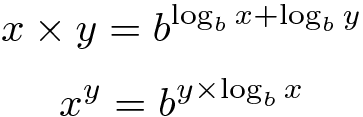
请注意,这些公式适用于除那个以外的任意正基b,因此我们可以选择便于实现的基。
在本文中,我们将展示如何在 Solidity 中有效地实现以 2 为底的对数和指数函数,如何将这些以 2 为底的函数转换为相应的自然(以e为底)函数,以及这些函数在 DeFi 应用程序中的实际用例是什么.
所以本文的重点是指数和对数。
对数
让我们从二进制(以 2 为底)对数开始。x的二进制对数是满足以下条件的值y:

显然,x的值必须为正才能使y存在。
请注意,如果
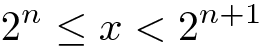
然后
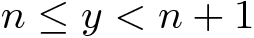
所以n是x的二进制对数的整数部分。因此,我们的第一个问题是:
Solidity中如何计算二进制对数的整数部分?
剧透:向右移动并计数。
这是适用于正整数x的简单方法:
for (n = 0; x > 1; x >>= 1) n += 1;虽然清晰简单,但这种方法非常昂贵,因为它的气体消耗为 O(n)。这是适用于 256 位正整数x的改进版本:
if (x >= 2**128) { x >>= 128; n += 128; }
if (x >= 2**64) { x >>= 64; n += 64; }
if (x >= 2**32) { x >>= 32; n += 32; }
if (x >= 2**16) { x >>= 16; n += 16; }
if (x >= 2**8) { x >>= 8; n += 8; }
if (x >= 2**4) { x >>= 4; n += 4; }
if (x >= 2**2) { x >>= 2; n += 2; }
if (x >= 2**1) { /* x >>= 1; */ n += 1; }这种改进的实现在最坏的情况下消耗了大约 600 gas:比原始的、未优化的少 25 倍。
到目前为止还不错,但是
如果 X 是小数怎么办?
剧透:只需添加指数。
Solidity 语言的核心中没有小数,但是有几种方法可以模拟这些数字。让我们考虑其中两种方式:二进制定点和二进制浮点。两种方式都表示小数x,如下所示:
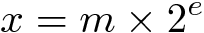
其中m和e是整数。值m称为尾数,e称为指数。二进制定点数和浮点数的区别在于,对于定点数,指数是预定义的常量,通常为负数,因此只需要存储尾数;而对于浮点数,指数是可变的,因此必须与尾数一起存储。
现在让我们注意,
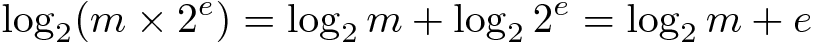
因此,二进制定点数或浮点数的二进制对数可以计算为尾数加上指数的二进制对数。只要指数是整数,同样的公式也适用于对数的整数部分。
现在,当我们知道如何为整数部分提供资金时,
二进制对数的小数部分呢?
扰流板:正方形和一半。
设n是x的二进制对数的整数部分,那么对数的小数部分可以这样计算:
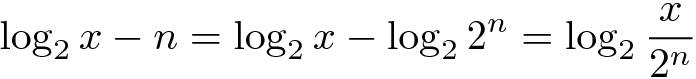
注意,只要
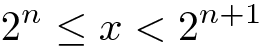
然后

因此,计算二进制对数的小数部分可以推导为计算 1(含)和 2(不含)之间数字的二进制对数。为了进行此计算,我们将使用以下两个规则:
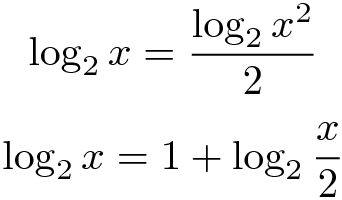
这是编写的代码,好像 Solidity 本身就支持小数:
for (delta = 1; delta >= precision; delta /= 2) {
if (x >= 2) { result += delta; x /= 2; }
x *= x;
}在每次迭代中,我们应用以前的规则:将 的值平方并将 的值x减半delta。如果在某个时刻 的值x变得大于或等于 2,那么我们将应用后一个规则:将 的值加起来delta并result减半x。我们重复循环直到delta下降到期望值以下precision,因为继续计算不会对result.
不幸的是,Solidity 本身不支持分数,所以真正的代码看起来像这样:
for (delta = ONE;
gte (delta, precision);
delta = div (delta, TWO)) {
if (gte (x, TWO)) {
result = add (resukt, delta);
x = div (x, TWO);
}
x = mul (x, x);
}其中ONE, TWO, add, mul, div, 和gte是常数和函数,模拟某种小数和对它们的算术以实现 Solidity。
幸运的是,ABDK 库已准备好对 64.64 位二进制定点四精度二进制浮点数使用二进制对数实现。
现在,当我们知道如何计算二进制对数时,
自然对数和常用对数呢?
剧透:魔法因素。
为了计算自然对数(以e为底)和常用对数(以 10 为底),我们可以使用以下规则:
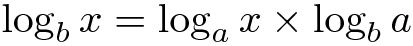
因此,
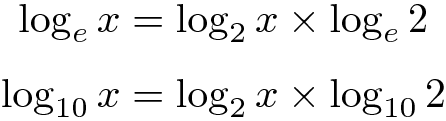
这里

是可以硬编码到实现中的神奇因素,不需要在运行时计算。
现在,当我们完成对数运算后,让我们切换到
指数
同样,让我们从以 2 为底的求幂开始,即计算

Solidity 有**权力的运营商,所以显而易见的解决方案是:
y = 2**x但是,这仅适用于x的那些值,即整数和非负值。此外,这不是最有效的方法,因为使用移位操作会更便宜一些:
y = 1 << x这种转变也可能有助于x的负值:
y = x >= 0 ? 1 << x : 1 >> -x由于 Solidity 本身不支持分数,任何负 x 都会导致零结果,这没有多大意义。但是,如果我们将此处的整数 1 替换为 1 的定点表示,则这段代码将变得更加合理。
对于二进制浮点数就更简单了,因为在上面的公式中,y是一个二进制浮点数,尾数等于 1,指数等于x。
到目前为止还不错,但是
如果 x 是小数怎么办?
剧透:倍增魔法因素。
让我们将x的小数值拆分为整数部分n和小数部分f:
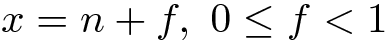
然后
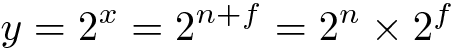
令f为二进制分数:
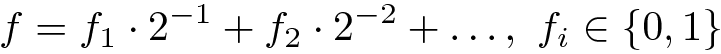
然后
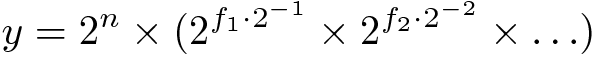
注意:
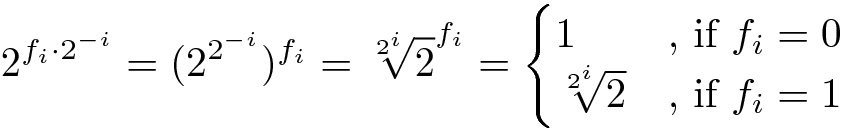
神奇的因素,

可以预先计算,不需要在运行时计算:

这很好,但是
我们应该预先计算多少魔法因子?
扰流板:尽可能多的精度位。
对于二进制定点数,答案很明显,因为小数点后的二进制位数是固定的。所以。如果不动点的小数部分有 64 位,那么我们需要 64 个魔法因子。
对于二进制浮点数,事情要复杂一些,因为尾数m可能会被大的负指数e移到最右边。因此,此类浮点数的二进制表示形式如下所示:

幸运的是,对于任何介于 0 和 1 之间的f,确实有

所以如果f是上面显示的二进制表示的数字,那么
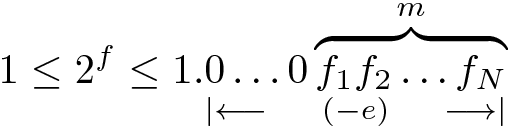
因此,如果所需的结果精度是M位,那么我们可以忽略f的二进制表示的那些位,这些位比点后的M个二进制位更远。这样我们最多需要预先计算M个魔法因子来计算指数。
可在ABDK 库源代码中找到二进制定点数和浮点数的基数 2 指数函数的即用型实现。
以 2 为底的指数很好,但是
任意基数的指数如何?
剧透:使用对数。
我们知道,对于任意正数x和任意正数b,以下情况成立:
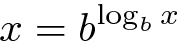
因此,对于任意y:
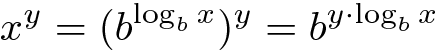
对于b =2 这给了我们:

由于我们已经知道如何计算以 2 为底的对数和指数函数,因此我们可以计算任意底数的指数函数。
该公式可用于有效地计算连续复利:
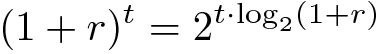
这里r是单个时间单位的利率,t是计算复利的时间间隔的长度。请注意,在固定利率的情况下,该值

可以只计算一次,可能是链下的,然后重复使用,这将使这个公式更加有效。
结论
在本文中,我们展示了如何在 Solidity 中针对二进制定点数和浮点数有效地计算以 2 为底的对数和指数函数。
我们还描述了如何通过 base-2 函数实现基于任意的对数和指数函数。
我们介绍了使用对数和指数函数有效实现的连续复利计算的真实用例。






![[QMT]03-让QMT支持从Tushare获取数据](https://img-blog.csdnimg.cn/img_convert/488eb5c3bb0755391c57635255de443d.png)