---

一、 因子的 IC 分析

• 判断因子与收益的相关性强度

• 分析结果

  • 因子平均收益
  • IC mean
  • IC std
  • IC > 0.02：IC大约0.02的比例，越大越严格
  • IR：信息比率（历史表现的稳定性）， IR = IC mean / IC std

2. 信息系数

• 定义：某一期的IC指的是 该期因子暴露度 和股票 下期的实际回报值 在横截面上的相关系数。
  

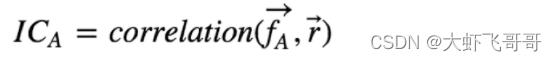
• 因子暴露度：因子本身数值

• 周期一天：该期的因子值（2023.1.11）、下期（2023.1.12）收益率（截面数据）

• 计算方式：斯皮尔曼相关系数（Rank IC）

  • 斯皮尔曼相关系数表明 X (独立变量) 和 Y (依赖变量)的相关方向。 如果当X增加时， Y 趋向于增加, 斯皮尔曼相关系数则为正。
  • 与之前的皮尔逊相关系数大小性质一样，取值 [-1, 1]之间。

• 信息系数API

  import scipy.stats as st
  
  st.spearmanr(fund['pe_ratio'], fund['return'])
  

• 收益率计算

• 因子的收益率分析
  • 确定因子的标的方向
  • 升序（因子越小越好）、降序（因子越大越好）、中性（方向不确定）

3. 举例

• 计算价差 每5分钟的 IC值 （5分钟为一个截面）

  • 获取 9 : 30 的 因子暴露值
  • 计算 9 : 35 的 收益率：return = (9:35 - 9:30) / 9:30
  • 计算相关系数

• IF 2212 和 IF2211 价差以及动量因子

求整个周期的IC值，为负值：

4. 因子处理

4.1 去极值

将极端值拉回到正常值（不是删除） 分位数去极值、中位数绝对偏差去极值、正态分布去极值。

• 分位数去极值

  • 中位数：大小排序，中间位置的数据
  • 四分位数：四等分（Q1、Q2、Q3）
  • 百分位数：25%分位数
  • 指定分位数外的异常点用分位数点替换

  from scipy.stats.mstats import winsorize
  winsorize(a, limits=0.25)  # 两端值
  

• 中位数绝对偏差去极值（推荐）

  • 找中位数

  • 每个因子与中位数的绝对偏差

  • 得到绝对偏差的中位数（MAD）

  • 按照MAD_e = 1.4826*MAD，然后确定参数n，做出调整

    def mad(factor):
        """
        三倍中位数去极值
        :param factor:
        :return:
        """
    
        med = np.median(factor)
        mad = np.median(abs(factor-med))
    
        high = med +(3 * 1.4826 * mad)
        low = med -(3 * 1.4826 * mad)
    
        factor = np.where(factor > high, high, factor)
        factor = np.where(factor < low, low, factor)
    
        return factor
    

• 正态分布去极值（很少使用）

  • 3 sigma原则

def three_sigma(factor):
    """
    正态分布去极值
    :param factor:
    :return:
    """
    mean = factor.mean()
    std = factor.std()

    high = mean + (3 * std)
    low = mean - (3 * std)

    factor = np.where(factor > high, high, factor)
    factor = np.where(factor < low, low, factor)

    std = StandardScaler()
    factor = std.fit(factor)

    return factor

4.2 标准化

def standard(factor):
    """
    新的X数据集方差为1，均值为0
    :param factor:
    :return:
    """
    # values = factor.values.reshape(-1, 1)
    # std = StandardScaler()
    # factor = std.fit_transform(values).T
    # return factor[0]

    mean = factor.mean()
    std = factor.std()
    factor = (factor - mean) / std

    return factor

4.3 市值中性化

防止选择的股票在固定的某些股票当中（因子受市值影响）

• 回归去除法

def remove_market_value(factor, market_value):
    """

    :param factor:
    :param market_value:
    :return:
    """
    from sklearn.linear_model import LinearRegression

    x = factor.reshape(-1, 1)
    y = market_value

    lr = LinearRegression()
    lr.fit(x, y)

    return factor - lr.predict(x)