目录

模式匹配

BF算法 

算法实现

算法分析

KMP算法

问题的引入（一）

问题的引入（二）

问题的引入（三）

相关概念

 计算失配函数的算法

算法思路

算法优点

---

模式匹配

函数int find(const sstring &t, int start )

从字符串（以下称主串s）的第start个位置的字符起，向后查找字符串t第一次在主串中出现的位置。如果在主串中找到该子串，返回其首次出现的位置，否则返回-1。

该操作相当于在主串的所有子串集合中匹配待查找的子串，因此该操作也被称作模式匹配。

模式匹配(亦称样品匹配)是各种串处理中最具有代表性的操作。一般被匹配串s称为主串，匹配串t称为模式。

设主串和模式t的串长度分别为n和m；主串值为“s0s1s2s3……sn-1”，模式值为“ t0t1t2t3……tm-1”，起始位置start = 0

模式匹配的两种算法：

Brute-Force(BF)算法

Knuth-Morris-Pratt(KMP)算法

BF算法 

算法实现

 以s =“SHANGHAI”，t=“HAI”为例，n=8，m=3。i指示主串当前字符的下标，j指示模式当前字符的下标。

 

//从串的第start个字符起，向后查找字符串t第一次在
//串中出现的位置找到返回位置序号，未找到返回 -1。
int sstring::BF_find(const sstring &t, int start )const
{ 
    int curStart; //每次比较时，主串的起始位置
    int i,j=0;   int pos=-1;//匹配不成功返回-1    int n, m;
     n = length();   m = t.length(); //主串长度和模式长度
     curStart=start;
 while (curStart<=(n-m))//剩余主串结点长度大于等于模式串长度
 {     i=curStart;
        while ((j<m)&&(str[i]==t.str[j])) {  i++;    j++; }
        if (j==m) {pos = curStart; break; }//匹配成功返回位置
        curStart++;    j=0;
   }
    return pos; 
}  

算法分析

最好情况：

主串从0下标开始比较整个模式即告成功，时间为O(m)

主串中每个位置上的字符都和模式中首字符不等，时间为时间为O(n)

最差情况：

主串从0下标一直到n-m下标开始和模式比较时，每次都是模式的最后一个字符不等，结果为匹配不成功；或者只有当主串从下标为n-m开始和模式比较相等，结果为匹配成功，时间均为        O((n-m)m)。

Knuth-Morris-Pratt(KMP)算法

问题的引入（一）

匹配时，前4个元素相同，第5个不同。因模式中元素各不相同，故下次可以让模式的第1个字符和主串的第5个字符开始比较，中间可以省略。

 根据模式中字符的特征+已经和主串中比较的结果，决定下次比较时主串的起始位置。

问题的引入（二）

匹配时，前4个元素相同，第5个不同。因模式中前4个元素均相同，故下次可以让模式的第4个字符和主串的第5个字符开始比较，中间可以省略。

 根据模式中字符的特征+已经和主串中比较的结果，决定下次比较时模式的起始位置。

问题的引入（三）

观察第三个例子

 根据模式中字符的特征+已经和主串中比较的结果，决定下次比较时模式的起始位置。

相关概念

前缀：一个串的前缀，是指从第1个字符开始到它的任意一个字符为止的子串。

对模式t= t0t1t2t3…tm而言，t0t1t2就是它的长度为3的前缀，t0t1t2t3t4就是它的长度为5的前缀。

失配：当主串中某字符和模式中某字符比较且不等时，称发生失配。主串中发生失配的位置称失配点。

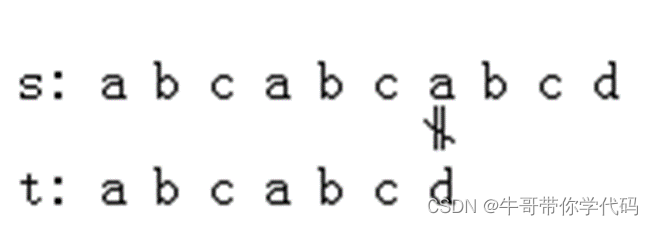注意：索引都是从0开始

最长前缀：图中，s6≠t6，发生失配。观察以模式失配点t6的前一字符t5为结束字符的子串，t0t1t2是它的一个前缀，而失配点t6前有一个子串t3t4t5，有t3t4t5=t0t1t2关系存在，称t0t1t2为该子串的最长前缀。假如模式串为r=“abcdsjtuabf”，则对字符f前的子串来说，最长前缀为r0r1即“ab”。

上图中，第二轮匹配可直接将主串失配点s6 和模式最长前缀t0t1t2的后一字符t3进行比较即可。由于t3 = s6，t4 = s7，t5 = s8，t6 = s9，这样就在主串中找到了模式t。

最长前缀获取：在实际应用中，主串通常比模式长得多，因此在模式匹配开始之前，值得花点时间将模式中字符的情况，完全分析清楚，因此这个任务是模式匹配前的首要任务。

失配函数：对模式中每一个位置上的字符，发现从开始到该位置前一字符形成的子串的最长前缀。下面用一个整型数组next[j]记录模式中第j个字符前子串的最长前缀的长度，以后将next称为失配函数。

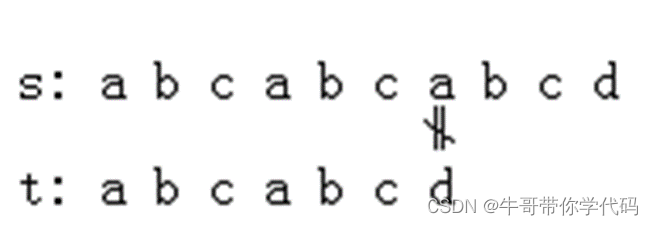
 计算失配函数的算法

//返回模式t的失配函数
int* nextValue(const sstring &t)
{
    int *next, m, i, j, k;

    m = t.length();
    if (m==0) return NULL;
    next = new int[m];
    next[0]=-1; next[1]=0;
for (j=2; j<m; j++)
    {   for (k=j-1; k>0; k--)
        {  for (i=0; i<k; i++)
                if (t.str[i]!=t.str[j-k+i]) break;
            if (i==k) break;
        }
        if (k==0)
            next[j] = 0;
        else
            next[j] = k;
    }
return next;
}

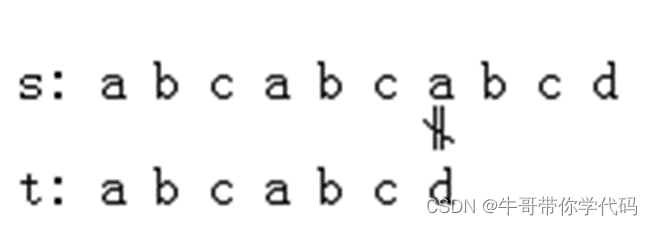
算法思路

假设主串s和模式t在匹配过程中，发生了失配，即tjt_j和sis_i不等。

假设以模式失配点的前一字符tj−1t_(j-1)为结束字符的子串的最长前缀长度为k，则主串s的失配点sis_i下一步只需和tkt_k继续比较下去就可以了。若tkt_k＝sis_i，则继续比较tk+1t_(k+1)和si+1s_(i+1)，如此继续进行，直至找到该模式，或者断定该模式不存在为止。

//从串的第start个字符起，向后
//查找字符串t第一次在串中出现
//的位置找到返回位置序号，未
//找到返回 -1。
int sstring::KMP_find(const sstring &t, int start )const
{
    int n = length(), m = t.length();
    int *next, curStart;
    int i,j;
    int pos=-1;

    next = nextValue(t); 
    //根据next数组中的值在主串中查找模式
    i=start; j=0;
    while (i<=(n-m))
    {  curStart = i-j;
        while ((j<m)&&(str[i]==t.str[j])){i++;j++;}
        if (j==m)
        {  pos=curStart;  break;   }
        else
        {  if (next[j]==-1) {++i;j=0;}
            else {j=next[j];}
        }
    }
    return pos;
}

计算失配函数，时间达O(m3)。

KMP算法，观察主串的指针i：

i开始为0，每次比较后，i不会减少，它或者不变或者增大1，直至n-m。

i不变的次数共有多少？：

如果本次开始匹配主串的第i个字符和模式中第1个字符相等，则i增加1；如果不等，本次模式匹配结束，下次模式匹配时i也增加1，故主串中每个i最多用2次，总体有2（n-m）次比较。

特殊地，如果模式的第1个字符和主串的第1个字符比较时总是不等，比较次数最少，为n-m次。

一般情况，m远小于n，KMP模式匹配算法时间复杂度为O(n)。

 算法优点

在硬盘当中寻找模式时，主串指针i不会变小(即不回溯)，是一个很大的优点。

设内存保存了模式和next数组，还保存了从硬盘读来的主串中一个扇区大小的字符串。假设第一个扇区的字符串同模式的相应字符串完全匹配了，下一步将读入第二个扇区的字符串到内存缓冲区，将第一个扇区的字符串覆盖掉；假设已在内存缓冲区中的第二个扇区的字符和模式进行匹配时，发生失配，用BF算法，就要将第一个扇区的字符串重新读入到内存缓冲区才可以继续匹配下去，重新读入非常费时，而KMP算法完全避免了这个缺点，是一个很好的算法。