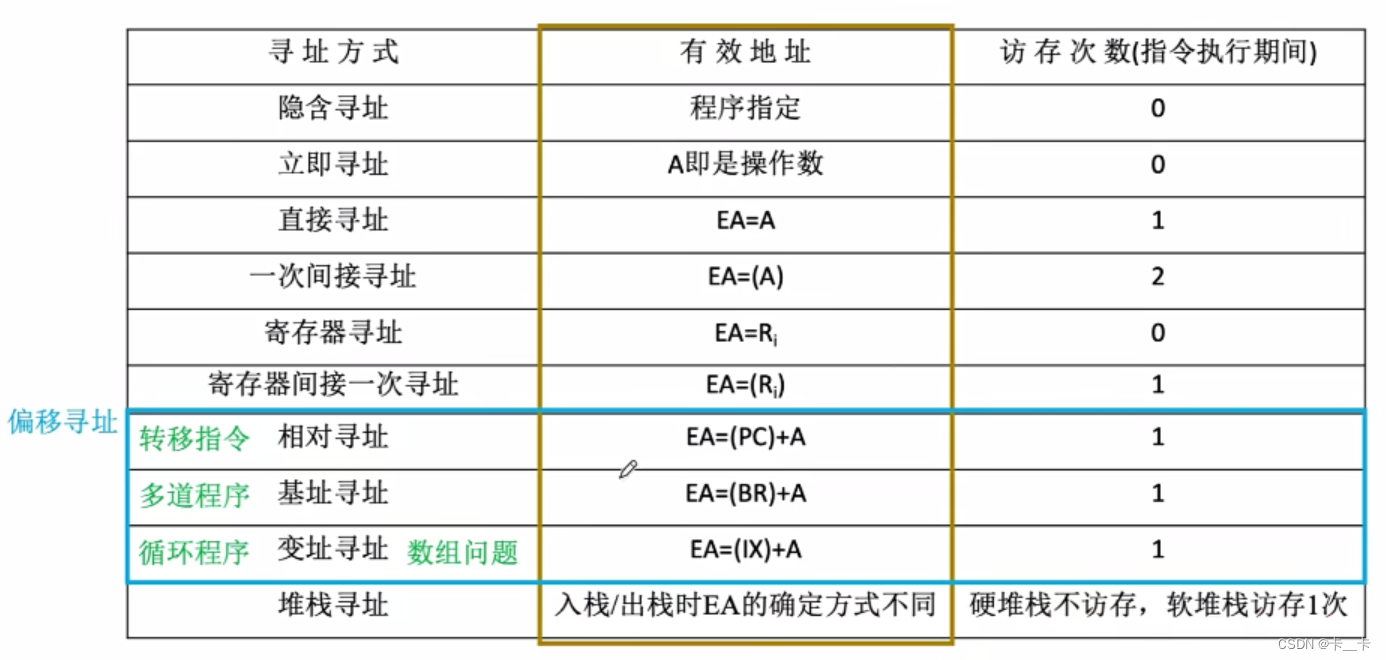
对于一个区间进行询问，进行修改，都是用线段树进行处理。
线段树和普通的树不一样，普通的树的节点存的是一个编号，线段树存的是一个区间，而且线段树一定是一棵完全二叉树。例如：
这就是一棵线段树。
例如对于[1...8](也就是1号根节点)这个节点来说，
[1...4](也就是2号节点)是它的lson(左儿子)
[5...8](也就是3号节点)是它的rson(右儿子)
并且和二叉树一样，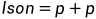
，
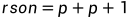(其中p为当前节点)
线段树可以给
区间加上某个值 
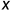，乘以某个值，覆盖某个值，取最大值 , 查询，单点查询，区间查询，查询和，查询最大最小值，查询区间最大字段和，查询各种奇怪的东西。(如果两个区间可以合并，所有的信息合并，那么就可以查询.
比如说区间最大字段和。
比如说我们找区间的最大字段和。
设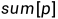
表示区间的最大字段和, 我们已知
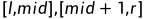的所有信息，我们要得到的所有信息。
所以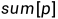
;
其中
表示前缀和的最大值，
表示后缀和的最大值。
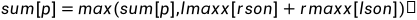
设tot[p]表示这一段的总和。
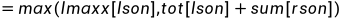
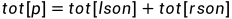
遍历时就用类似二分的做法枚举区间就行了
（其实蛮简单的）
例题：单点修改，区间查询
一道模板题，详见代码：
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+10;
#define ls p+p//左儿子
#define rs p+p+1//右儿子
long long sum[maxn*4],ans;//记得开4倍
int a[maxn],n,q;
void update(int p){
sum[p]=sum[ls]+sum[rs];//因为是加和，所以当前节点为它的左右儿子的和
}
void build(int p,int l,int r){//建树，分别表示当前节点编号，区间左端点和右端点
if(l==r) {//如果到了叶子节点
sum[p]=a[l];//初值
return;
}
int mid=l+r>>1;
build(ls,l,mid);
build(rs,mid+1,r);
update(p);
}
//a[x]+=v;
void change(int p,int l,int r,int x,int v){//更改，参数同上
if(l==r&&l==x){//如果是这个要加的节点
sum[p]+=v;
return;
}
int mid=l+r>>1;
if(x<=mid)change(ls,l,mid,x,v);
else change(rs,mid+1,r,x,v);
update(p);//记得更改
}
void query(int p,int l,int r,int x,int y){
if(x<=l&&r<=y) {//如果是这个区间
ans+=sum[p];//加上答案
return;
}
int mid=l+r>>1;
if(x<=mid)query(ls,l,mid,x,y);
if(y>mid)query(rs,mid+1,r,x,y);
}
int main(){
cin>>n>>q;
for(int i=1;i <=n;i++)cin>>a[i];
build(1,1,n);
while(q--){
int a,b,c;
cin>>a>>b>>c;
if(a==1)change(1,1,n,b,c);
else{
ans=0;
query(1,1,n,b,c);
cout<<ans<<endl;
}
}
}
如果是要求区间最大/值的话，就修改update函数就行了。
那如何进行区间修改呢？
那需要打上lazy标记。
比如只有区间加法。 那么你应该修改change函数和query函数，
并增加一个push操作，用来下传标记。
如果还是不明白懒标记的话，
就去看这个吧
void change2(int p,int l,int r,int x,int y,int z) {
if(x<=l&&r<=y){
sum[p]+=(r-l+1)*z;//当前节点应+=区间长度*懒标记
add[p]+=z;//加上懒标记
return;
}
int mid=l+r>>1;
if(x<=mid)change2(ls,l,mid,x,y,z);
if(y>mid)change2(rs,mid+1,r,x,y,z);
update(p);
}
void push(int p,int l,int r){//一般的区间加法的标记传递
int mid=l+r>>1;
sum[lson]+=(mid-l+1)*lazy[p];
sum[rson]+=(r-mid)*lazy[p];
lazy[ls]+=lazy[p];//记得把标记传递下去。
lazy[rs]+=lazy[p];
lazy[p]=0;//标记使用过后要清空。
}
void query(int p,int l,int r,int x){
if(l==r){
更新答案
return;
}
push(p,l,r);//传递标记
int mid=l+r>>1;
if(x<=mid)query(lson,l,mid,x);
else query(rson,mid+1,r,x);
}
我相信你一定会觉得线段树灰常简单的，对吧？
