A. Hard Way
题目链接:Problem - A - Codeforces

样例输入:
5
8 10
10 4
6 2
4 6
0 1
4 2
14 1
11 2
13 2
0 0
4 0
2 4
0 1
1 1
0 0
样例输出:
0.0000000
0
2.0000
0.00
1
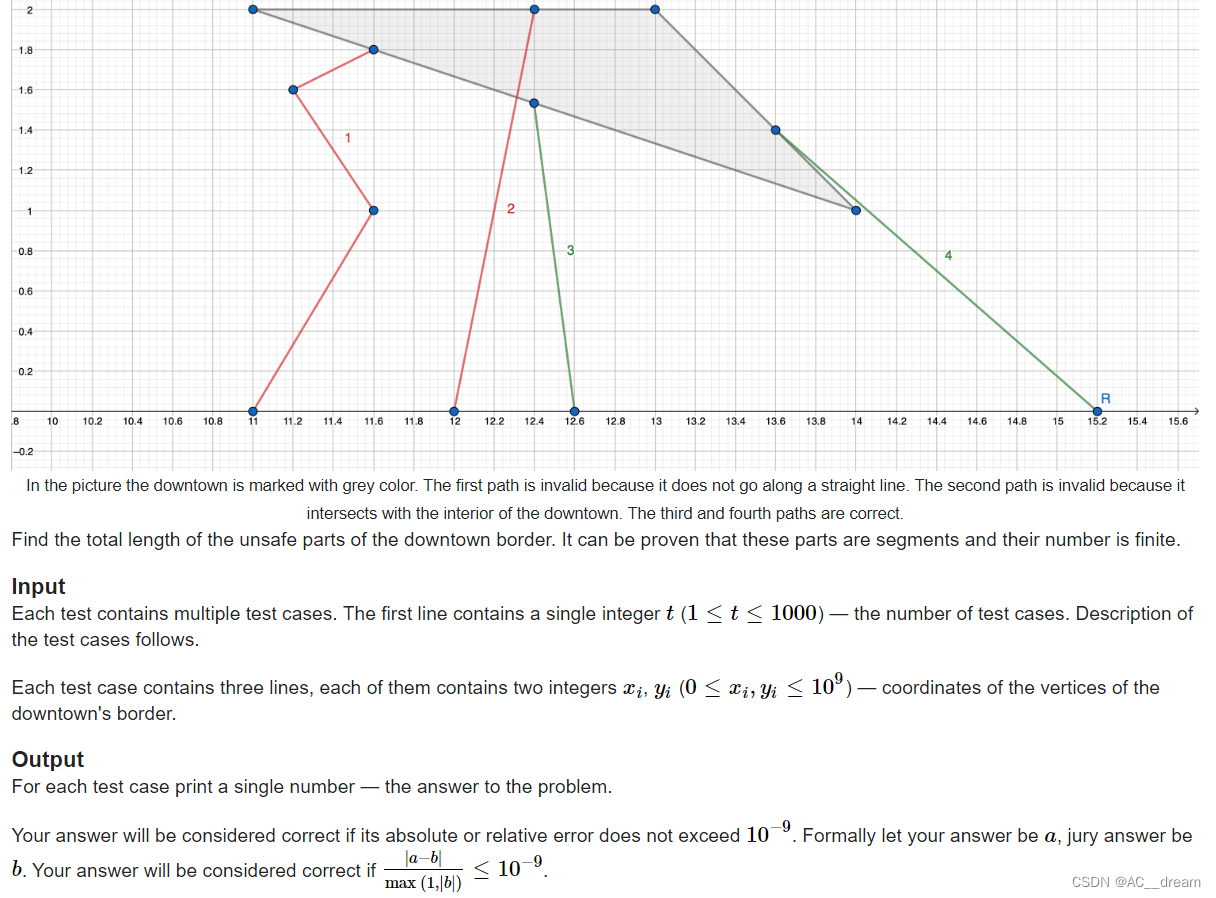
题意:给定一个三角形的三个顶点,输入保证三角形的三个顶点是合法的,然后让我们找出满足从x轴上一点向三角形边界上一点连线必须经过三角形内部的点的集合的长度,只要在x轴上存在任意一个点即可。
分析:容易发现,只要是一边斜率不为0那么就一定能够在x轴上找到一个点使得从这一点向三角形该边上一个点连边不经过三角形内部,这个画一下图就很容易发现。那么是不是对于所有的斜率为0的边上的一点与 就一定需要经过三角形内部吗,其实也不一定,如果三角形的斜率为0的边是三角形纵坐标最小的那一条边,那么这条边肯定是不满足题意的,因为这个肯定不需要经过三角形内部,综合以上情况,就是要求斜率为0的边而且纵坐标不是最小的那条边的长度。
代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<vector>
#include<queue>
using namespace std;
const int N=2e5+10;
int x[5],y[5];
int main()
{
int T;
cin>>T;
while(T--)
{
int ans=0;
for(int i=1;i<=3;i++)
scanf("%d%d",&x[i],&y[i]);
x[4]=x[1];y[4]=y[1];
for(int i=2;i<=4;i++)
if(y[i]==y[i-1]&&y[i]==max(max(y[1],y[2]),y[3]))
ans=abs(x[i]-x[i-1]);
printf("%d\n",ans);
}
return 0;
} B. Power Walking
题目链接:Problem - B - Codeforces

样例输入:
2
3
1 1 2
6
5 1 2 2 2 4
样例输出:
2 2 3
4 4 4 4 5 6
题意:现在有n个数,我们要将其随意划分至k个集合,每个集合至少要有一个元素,每个集合的贡献就是这个集合内不同数的个数,现在要我们求得k个集合的贡献和最小是多少,输出n个值,分别对应着k=1,2……,n的情况。
分析:我们先分析一下n个元素中到底存在多少种值不相同的元素,不妨是t,那么无论划分为多少个集合都不可能使得所有集合的贡献和小于t,但是我们能保证当k<=t时,我们总能找到一种方案使得集合的总贡献是等于t的,就是对于值相同的元素我们尽可能把其划分至同一个集合,从而减少这个值对所有集合的贡献和,对于k>t的情况,每多一个集合我们不得不拿出来一个数放入一个新的集合,那么他的贡献就会在原来的基础上+1,一直到划分为n个集合为止,当划分为n个集合时每个集合的贡献都是1,总贡献是n,这样也刚好符合我们的预期。
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<vector>
#include<queue>
#include<set>
using namespace std;
const int N=2e5+10;
int main()
{
int T;
cin>>T;
while(T--)
{
set<int>s;
int n;
scanf("%d",&n);
int t;
for(int i=1;i<=n;i++)
{
scanf("%d",&t);
s.insert(t);
}
int m=s.size();
for(int i=1;i<=m;i++)
printf("%d ",m);
for(int i=m+1;i<=n;i++)
printf("%d ",i);
puts("");
}
return 0;
}C. Great Sequence
题目链接:Problem - C - Codeforces

样例输入:
4
4 4
1 16 4 4
6 2
1 2 2 2 4 7
5 3
5 2 3 5 15
9 10
10 10 10 20 1 100 200 2000 3
样例输出:
0
2
3
3
题意:给定一个长度为n的数组a和一个正整数x。问至少需要向原数组中添加多少个数才能够使得操作后的数组可以两两配对使得每一对中的一个数是另一个数的x倍,每次向数组中添加的数可以为任意值。
分析:这个思路就很好想了,我们先把原数组中可以配对的数先进行配对,剩余的数我们没办法再完成配对,只能选择加入一个数来完成该数的配对,所以我们就是要求最少不能配对的数的个数。
那么这个我们直接暴力进行配对,对于每一个待配对的数y,我们都看一下x*y是否存在即可,如果存在就进行配对,否则就加入一个数完成配对。但是我们进行暴力配对的时候一定要从小到大进行,避免出现这种情况,比如x=2,原数组是2,4,8,16,我们先把4和8进行配对,那么剩余的2和16都不能进行配对,从而使得答案为2,但实际上我们应该先让2和4进行配对,然后让8和16进行配对,这样就没有不能配对的数了。
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<vector>
#include<queue>
#include<map>
using namespace std;
const int N=2e5+10;
int main()
{
int T;
cin>>T;
while(T--)
{
map<long long,int>mp;
int n,x;
scanf("%d%d",&n,&x);
long long t;
for(int i=1;i<=n;i++)
{
scanf("%lld",&t);
mp[t]++;
}
int ans=0;
for(auto t:mp)
{
if(!mp.count(t.first*x))
{
ans+=t.second;
continue;
}
int p=min(t.second,mp[t.first*x]);
mp[t.first*x]-=p;
ans+=t.second-p;
}
printf("%d\n",ans);
}
return 0;
}D. Repetitions Decoding
题目链接:Problem - D - Codeforces

样例输入:
4
2
5 7
2
5 5
6
1 3 1 2 2 3
6
3 2 1 1 2 3
样例输出:
-1
0
1
2
4
1 3
5 3
5 3
10 3
2
8 6
5
0 3
8 3
5 3
6 2
7 1
4
2 6 6 2题意:给定一个长度为n的数组,我们可以对这个数组进行操作,每次选择一个位置,可以在这个位置插入两个数,这两个数必须相同,问我们的操作方案使得操作后的数组可以分成若干个tandem repeats,还需要输出每一个tandem repeats的长度,每个tandem repeats是一个字符串,需要满足长度为偶数而且前半段与后半段完全相同,比如123123就是一个tandem repeats。
分析:由于我们每次都是向数组中同一个位置加入两个相同的数,所以每个数的奇偶性是不会发生改变的,由于tandem repeats的定义我们不难发现,对于tandem repeats中的每一个数的出现次数必须为偶数,所以一开始我们需要判断一下整个数组中有没有一个数的出现次数为奇数的,如果有就直接输出-1.否则我们就需要找到构造出一种方案。
构造方式如下:
以 1 3 1 2 2 3为例:
我们发现第一个1在之后的出现位置为3,那么我们就那这部分进行构造:
1 3 1->1 3 1 3 3
这样构造完1 3 1 3就是一个符合题意的tandem repeats,然后把多出来的3放置后面
剩余的数组为 3 2 2 3
我们发现第一个3在之后的出现位置为4,那么我们就对这部分再进行构造
3 2 2 3 ->3 2 2 3 2 2->3 2 2 3 2 2 2 2
也许会有同学有疑问:在后面添加两次2就已经满足题意了,为什么还要再添加两个2呢?其实这是因为两个2相邻是一种特殊情况,我们为了构造的一般性这里就不对这个进行优化了,毕竟题目中并没有要求最少操作次数,所以我们可以加两次2,需要注意,第二次加入2是加入到第一次加入的两个数中间,对于两次加入的都是同一个数当然没有影响,但是如果要是不同的数就会产生影响,比如先后加入2和3得到的操作序列的变化是2 2->2 3 3 2,下次如果还想加入什么数就加入到上一次操作后的两个数中间,这样我们就可以按照这个方法构造我们想要的任意序列了。这个时候有同学可能会问:这样真的一定能构造出来吗?答案是YES,因为假如我们每次选定的数组长度为n,那么我们就会操作n-2次,那么我们除掉已经构造好的tandem repeats,剩余的数组长度会减少2,而且保证每个数的出现次数为偶数,那么数组第一个数在后面一定还会出现,所以这样一定是可行的,空间复杂度是O(n^2)的。
细节比较多,见代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<vector>
#include<queue>
#include<map>
using namespace std;
const int N=1e7+10;
int a[N];
int b[N];
int main()
{
int T;
cin>>T;
while(T--)
{
vector<int> len;
vector<int> p;
vector<int> val;
map<int,int>mp;
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]),mp[a[i]]++;
bool flag=true;
for(int i=1;i<=n;i++)
if(mp[a[i]]&1)
{
flag=false;
break;
}
if(!flag)
{
puts("-1");
continue;
}
int id=1;
for(int i=1;i<=n;i+=2)
{
int j=i+1;
while(j<n&&a[j]!=a[i]) j++;
if(i+1==j&&j==n)
{
len.push_back(2);
break;
}
int l=j-i;
for(int k=i+1;k<j;k++) b[k]=a[k];
for(int k=1;k<l;k++)
{
p.push_back(id+l+k-1);
val.push_back(a[i+k]);
}
for(int k=1;k<l;k++)
a[i+k+1]=b[i+l-k];
len.push_back(l*2);
id+=l*2;
}
printf("%d\n",p.size());
for(int i=0;i<p.size();i++)
printf("%d %d\n",p[i],val[i]);
printf("%d\n",len.size());
for(int i=0;i<len.size();i++)
printf("%d ",len[i]);
puts("");
}
return 0;
}