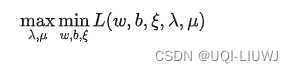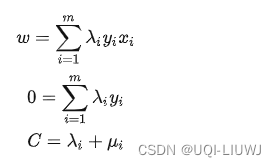1 一些概念
1.1 线性可分
- 在二维空间上，两类点被一条直线完全分开叫做线性可分。
- 严谨的说法是：
- D0和 D1 是 n 维欧氏空间中的两个点集。
- 如果存在 n 维向量 w 和实数 b，使得所有属于 D0 的点 xi 都有 wxi+b>0 ，而对于所有属于 D1 的点 xj 则有 wxj+b<0 ，则我们称 D0 和 D1 线性可分。
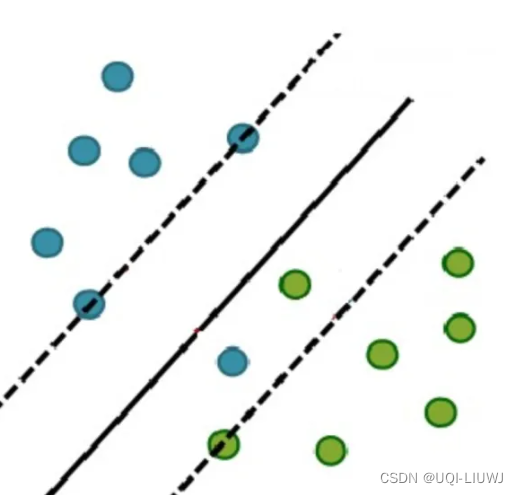
1.2 最大间隔超平面
但是，问题来了，如果有很多的超平面可以分割这两类点，那么应该选择哪一条呢
答案是找最佳超平面，以最大间隔把两类样本分开的超平面，也称之为最大间隔超平面。
- 两类样本分别分割在该超平面的两侧；
- 两侧距离超平面最近的样本点到超平面的距离被最大化了。
1.3 支持向量
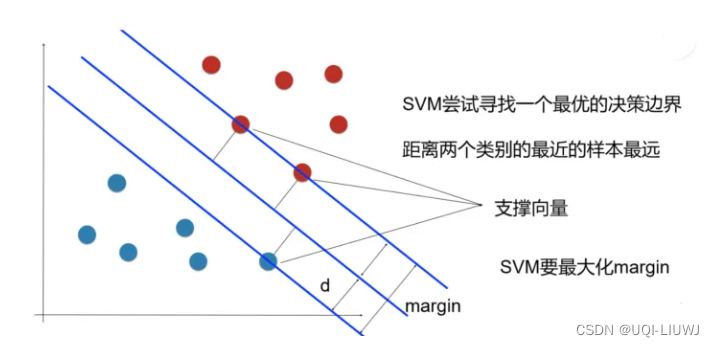
- 样本中距离超平面最近的一些点，这些点叫做支持向量
1.4 点到直线的距离
二维空间点 (x,y) 到直线 Ax+By+C=0 的距离为：
2 SVM
2.1 最优化问题
2.1.1 支持向量到超平面距离推导
- SVM 希望找到各类样本点到超平面的距离最远，也就是找到最大间隔超平面
- 我们记某一超平面为：
- 则点
到超平面
的距离为：
- 则点
-
于是我们有：
-
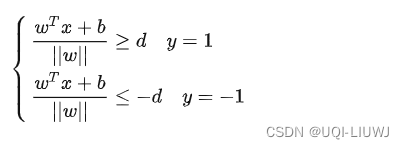
即：
-
||w||d是正数，且令其为任何值都不会对优化结果有影响
-
——>不妨令||w||d=1
-
所以有
-
-
将方程组合并，有：
（等于1的地方就是支持向量）
2.1.2 最优化问题目标函数
通过上一小节我们知道：
- 支持向量处
-
点
-
——>支持向量到超平面的距离是
-
——>margin=
我们希望最大化margin，即;
分子分母调换位置，有：
此时计算||w||时要带根号，为了方便计算，我们将上式改写成
所以最优化问题是
2.2 最优化问题求解
目前SVM问题是一个带不等式的最优化问题
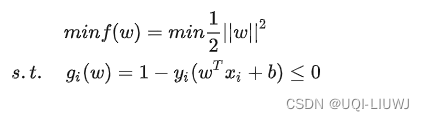
数学知识笔记：拉格朗日乘子_UQI-LIUWJ的博客-CSDN博客
根据KKT条件，我们有
2.3 最优化问题对偶问题
根据数学知识笔记：拉格朗日乘子_UQI-LIUWJ的博客-CSDN博客
我们可以写出原始问题
的对偶形式：
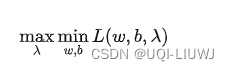（λ≥0）
2.3.1 求解过程
- 先看里面 min 部分，对w和b求偏导：
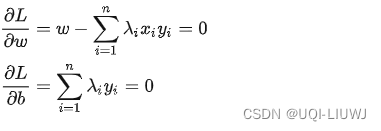
- 得到：
- 带回到L(w,b,λ)中，有：
——>去掉min一层，对偶问题就转化为：
之后利用SMO(Sequential Minimal Optimization) 算法求解各个λ，然后通过λ求W
W求得后，可以求解b：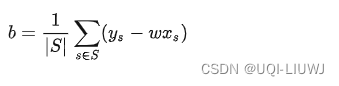
（S为支持向量的集合）
3 软间隔
3.1 不完全线性可分问题
完全线性可分的样本是很少的，如果遇到了不能够完全线性可分的样本，应该怎么办？
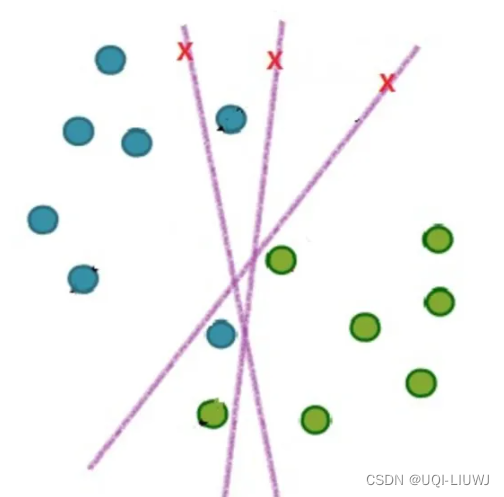
3.2 软间隔
相比于硬间隔的苛刻条件，软间隔允许个别样本点出现在间隔带里面
引入松弛变量从原来硬间隔的
变成
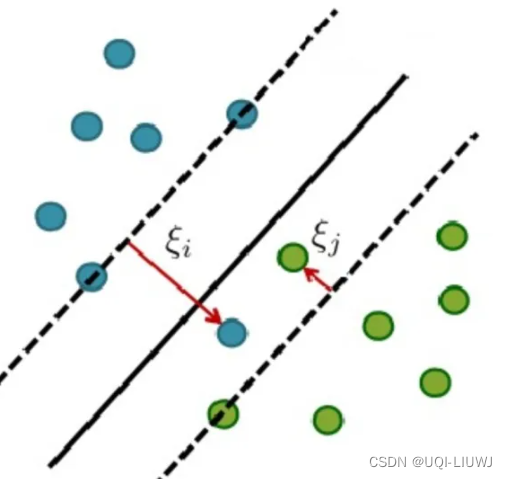
3.2.1 软间隔优化问题
- 增加软间隔后，优化目标变成了：
- C 是一个大于 0 的常数，可以理解为错误样本的惩罚程度
- 若 C 为无穷大， ξi 必然无穷小，如此一来就又变成了线性可分 SVM
- 当 C 为有限值的时候，会允许部分样本不遵循约束条件。
3.2.2 软间隔拉格朗日函数
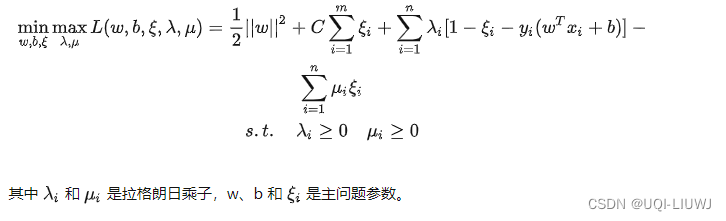
3.2.3 软间隔对偶问题
分别对主问题参数w、b 和 ξi 求偏导数，并令偏导数为 0，得出如下关系：
将这些关系带入拉格朗日函数中，得到：
最小化结果只有 λ 而没有 μ ，所以现在只需要最大化 λ 就好：
这个和硬间隔的一样，只是多了个约束条件。
同样地， 之后利用SMO(Sequential Minimal Optimization) 算法求解各个λ，然后通过λ求W
W求得后，可以求解b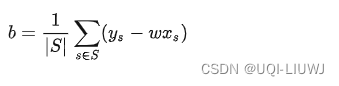：（S为支持向量的集合，这里间隔内的那部分样本也是支持向量）
4 非线性SVM
前面讨论的硬间隔和软间隔都是在说样本的完全线性可分或者大部分样本点的线性可分。
但我们可能会碰到的一种情况是样本点不是线性可分的，比如：
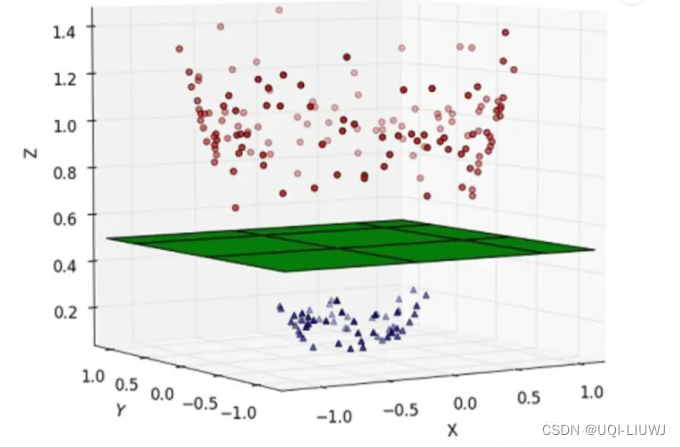
这种情况的解决方法就是：将二维线性不可分样本映射到高维空间中，让样本点在高维空间线性可分，比如：
对于在有限维度向量空间中线性不可分的样本，我们将其映射到更高维度的向量空间里，再通过间隔最大化的方式，学习得到支持向量机，就是非线性 SVM。
我们用 x 表示原来的样本点，用 ϕ(x) 表示 x 映射到特征新的特征空间后到新向量。那么分割超平面可以表示为： f(x)=wϕ(x)+b 。
对于非线性 SVM 的对偶问题就变成了：
可以看到与线性 SVM 唯一的不同就是：之前的 (xi⋅xj) 变成了 (ϕ(xi)⋅ϕ(xj)) 。
4.1 非线性SVM VS 线性SVM
- 不难发现，如果不使用对偶形式的话，映射关系的计算和存储也是一个大问题
5 多分类问题
参考内容：【机器学习】支持向量机 SVM（非常详细） - 知乎 (zhihu.com)
