图的矩阵表示

1 关联矩阵

定义：设无向图G=<V,E>,V={$v_1,v_2,\cdot \cdot \cdot ,v_n$},E={$e_1,e_2,\cdot \cdot \cdot ,e_m$},令$m_{ij}$为顶点$v_i$与边$e_j$的关联次数，则称$(m_{ij}{)}_{n\times m}$为G的关联矩阵，记作M(G)。
例如： 无向图的关联矩阵为

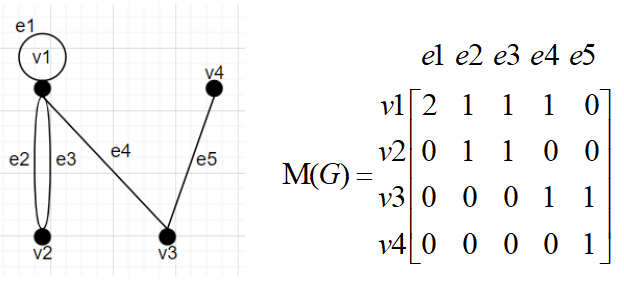
结论：矩阵的数值为顶点与边的关联次数

2 邻接矩阵

定义：设无向图G=<V,E>,V={$v_1,v_2,\cdot \cdot \cdot ,v_n$},令$a_{ij}$为顶点$v_i$邻接到顶点$v_j$的边的条数，称$(a_{ij}{)}_{n\times m}$为D的邻接矩阵，记作A(D)，或简记为A。
有向图D的邻接矩阵为：

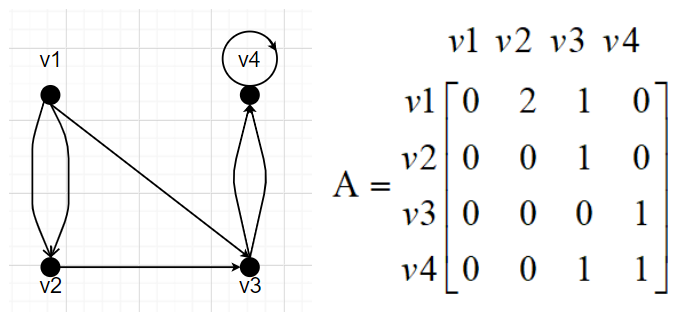
可以得出$A^2,A^3,A^4$:

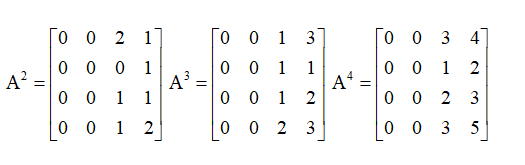
不难看出，D中$v_2$到$v_4$的长度为1，2，3，4的通路分别为0，1，1，2条。$v_4$到自身长度为1，2，3，4的回路分别为1，2，3，5条，D中长度小于等于4的通路有53条，其中有15条回路。
结论：A为$v_i$到达$v_j$长度为1的条数；$A^2$为$v_i$到达$v_j$长度为2的条数;$A^3$为$v_i$到达$v_j$长度为3的条数;$A^4$为$v_i$到达$v_j$长度为4的条数

3 可达矩阵

定义：设无向图G=<V,E>,V={$v_1,v_2,\cdot \cdot \cdot ,v_n$},令
$P_{ij}\{\begin{array}{ll}a& v_i可达v_j\\ c& 否则\end{array}$
称$P_{ij}$为D的可达矩阵，记作P(D),简记为P
有向图D的可达矩阵为：

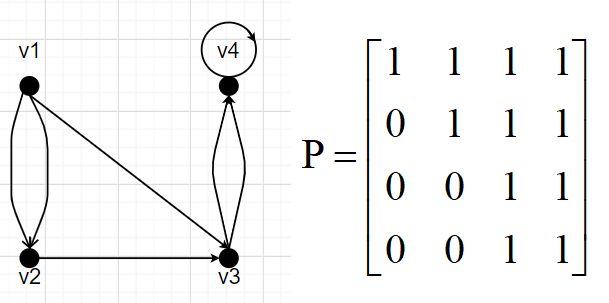
结论：$v_i$能否到达$v_j$