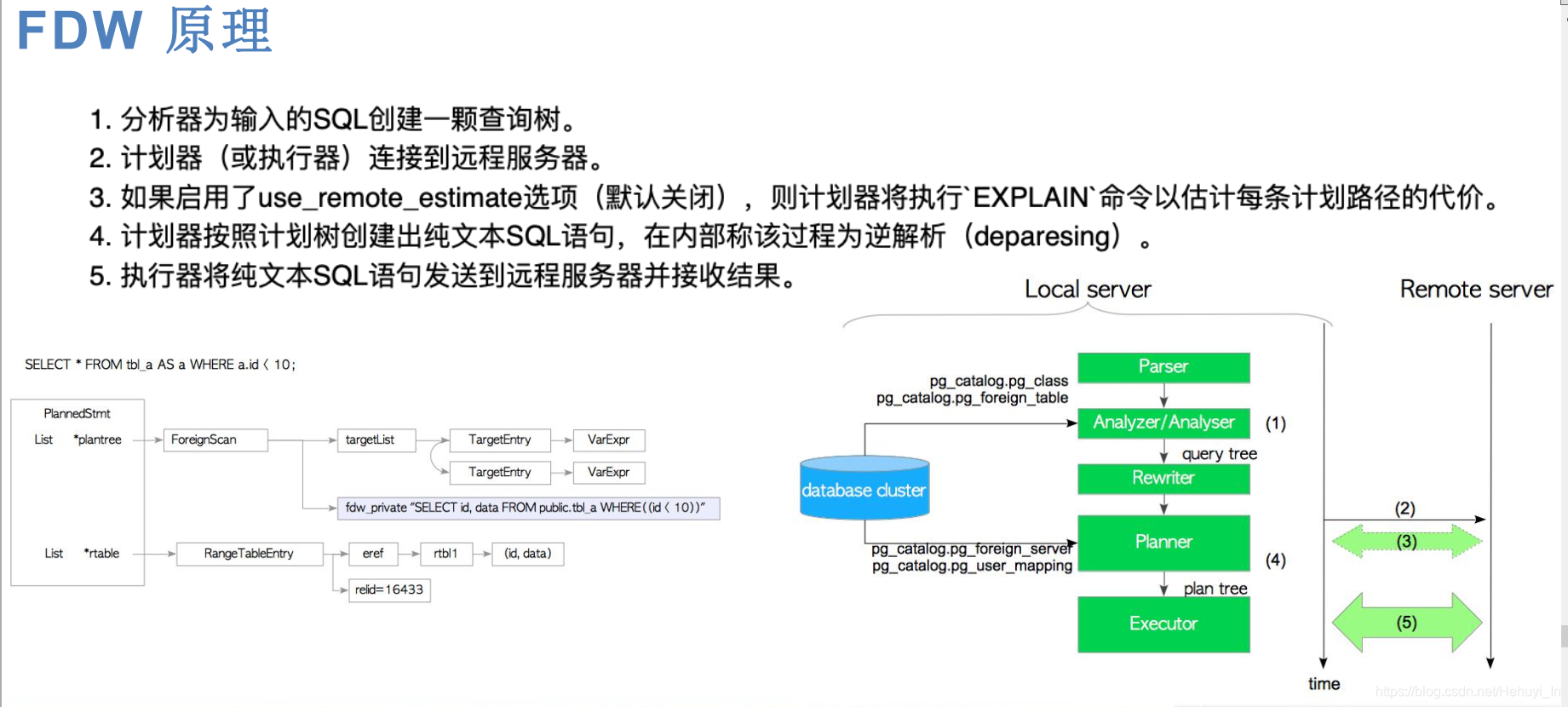
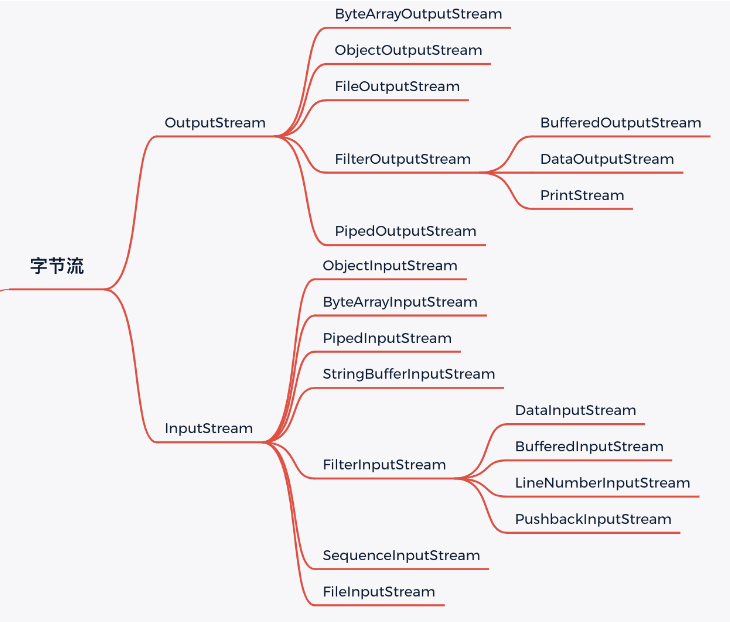
4、树和二叉树

逻辑结构

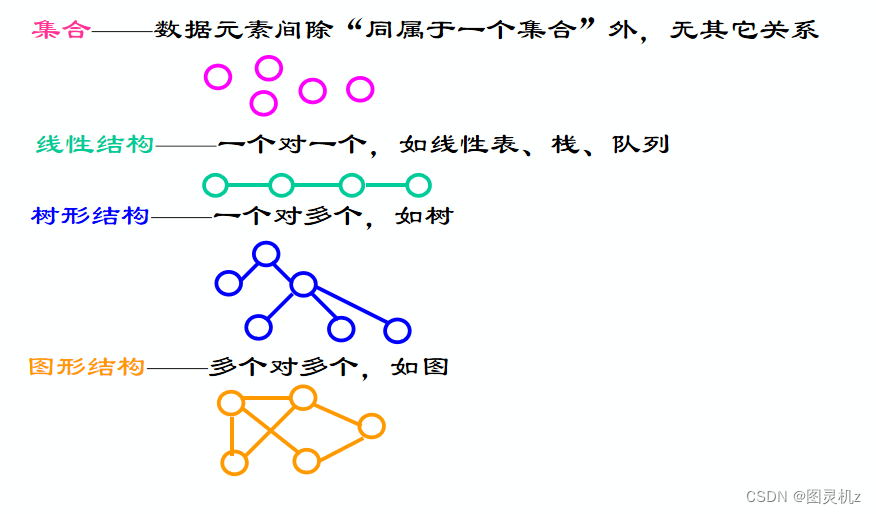
4.1、树的定义和基本术语

树是n个结点的有限集

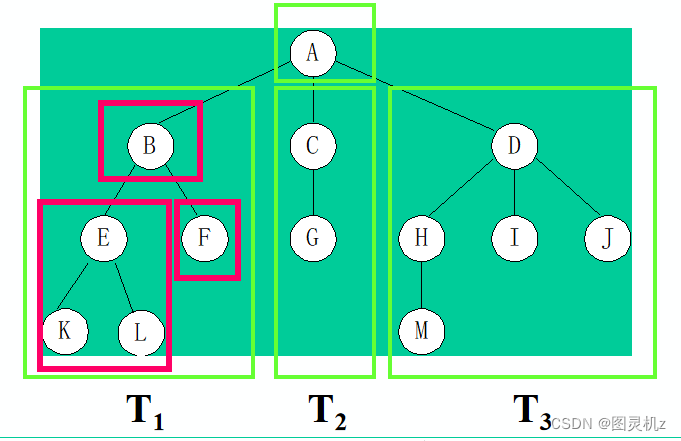
树的其他表示方式

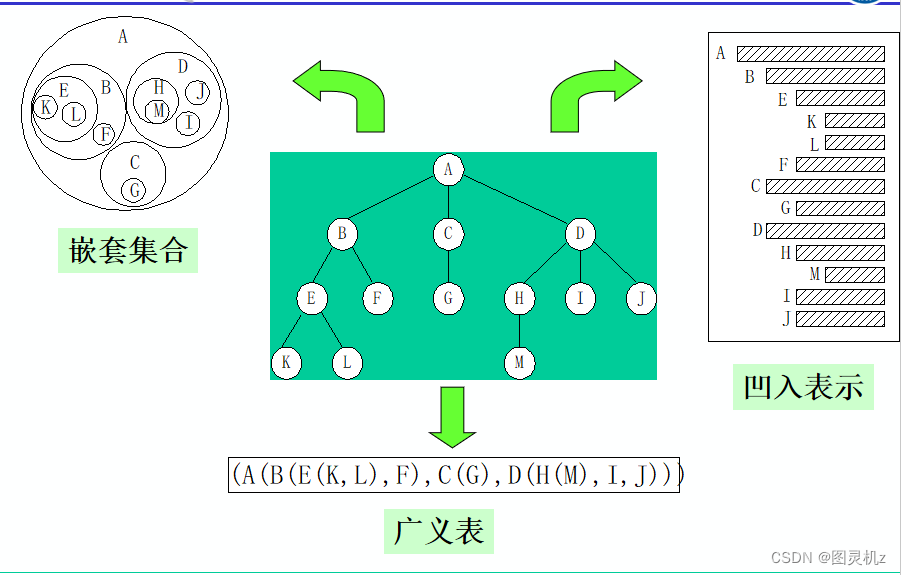
基本术语

根——即根结点（没有前驱）

叶子——即终端结点（没有后继）

森林——指m棵不相交的树的集合（例如删除根节点A后的子树）

有序树——结点各子树从左至右有序，不能互换（左为第一）

无序树——结点各子树可互换位置

双亲——即上层的那个结点（直接前驱）

孩子——即下层结点的子树的根（直接后继）

兄弟——同一双亲下的同层结点（孩子之间互称兄弟）

堂兄弟——即双亲位于同一层的结点（但并非同一双亲——

祖先——即从根到该结点所经分支的所有结点

子孙——即该节点下层子树中的任一结点

结点——即树的数据元素

结点的度——结点挂接的子树数

结点的层次——从根到该结点的层数（根结点算第一层）

叶子结点——即度为0的结点

内结点——即度不为0的结点

树的度——所有结点度中的最大值

树的深度（或高度）——指所有结点中最大的层数

4.2、二叉树

普通树（多叉树）若不转化为二叉树，则运算很难实现

为何要重点研究每结点最多只有两个“叉”的树？

• 二叉树的结构最简单，规律最强

• 可以证明，所有树都能转为唯一对应的二叉树，不失一般性

二叉树的基本特点

• 结点的度小于等于2
• 有序树（子树有序，不能颠倒）

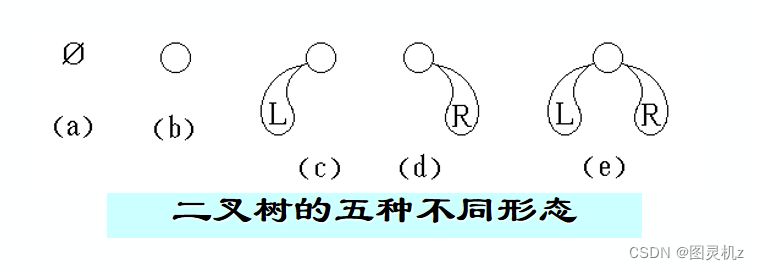
二叉树的性质

性质1：在二叉树的第i层上至多有2^i-1个结点

第i层上至少有1个结点

性质2：深度为k的二叉树至多有(2^k)-1个结点

深度为k时至少有k个结点

性质3：对于任何一棵二叉树，若2度的结点有n2个，则叶子树n0必定为n2+1（即n0=n2+1)
$$B=n-1$$

$$B=n_2\times 2+n_1\times 1$$

$$n=n_2\times 2+n_1\times 1+1=n_2+n_1+n_0$$

特殊形态的二叉树

满二叉树：一棵深度为k且有(2^k)-1个结点的二叉树。（特点：每层都“充满”了结点）

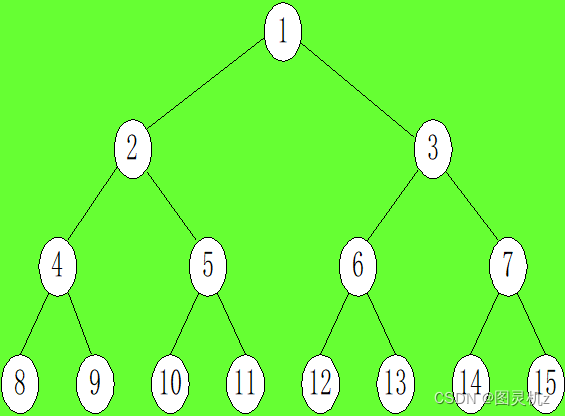
完全二叉树：深度为k的，有n个结点的二叉树，当且仅当其每一个结点都与深度为k的满二叉树中编号从1至n的结点一一对于

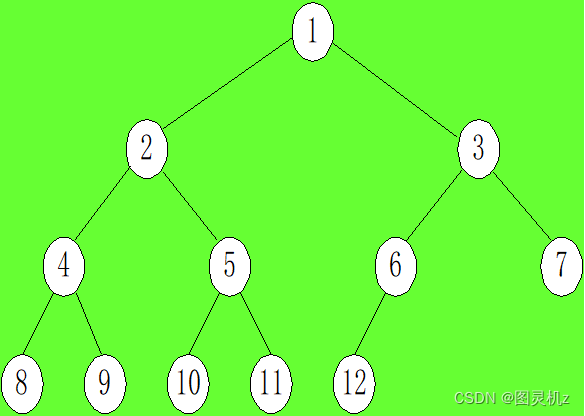
问题：一个有5000个结点的完全二叉树的叶结点个数是（2500）。

解：

设二叉树中度为0结点个数为n0,度为1的结点个数为n1,度为2的结点个数为n2
于是 n0 + n1 + n2 = 500,由二叉树性质n0 = n2 + 1,代入得到：2n2 + 1 + n1 = 5000
显然n1是奇数,考虑到完全二叉树中度为1结点个数最多为1,因此n1 = 1
因此n2 = 2499,n0 = 2500,只有左孩子的结点个数为1
考虑到完全二叉树中没有结点只有右孩子,因此只有右孩子的结点个数为0

**性质4：**具有n个结点的完全二叉树的深度必为[logn]+1

性质5: 对完全二叉树，若从上至下、从左至右编号，则编号为i 的结点，其左孩子编号必为2i，其右孩子编号必为2i＋1；其双亲的编号必为i/2。

一个有3999个结点的最大堆对应的完全二叉树的最后一个内结点的编号是（1999）。
（奇数个节点的完全二叉树最后一个内节点的编号是度为2的个数）

二叉树的顺序存储

实现：按满二叉树的结点层次编号，依次存放二叉树中的数据元素。

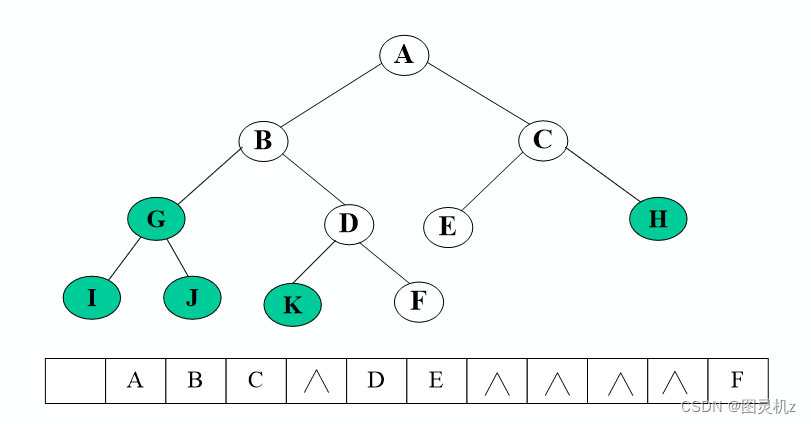
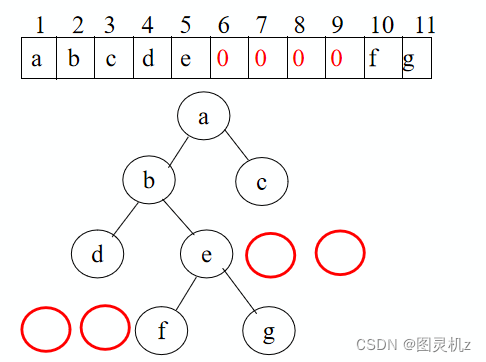
特点：结点间关系蕴含在其存储位置中，浪费空间，适于存满二叉树和完全二叉树

二叉树的链式存储

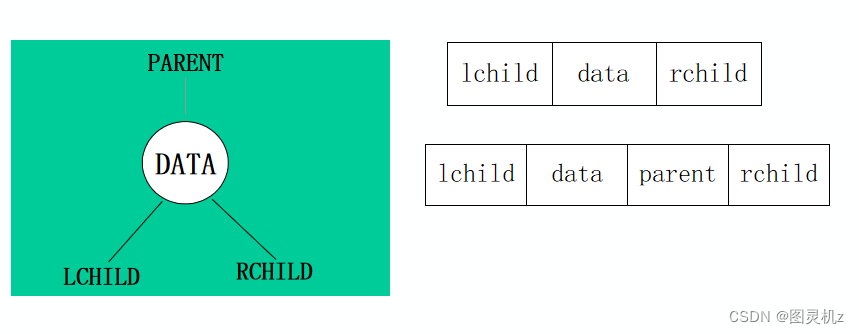
二叉链表：只有左右孩子指针

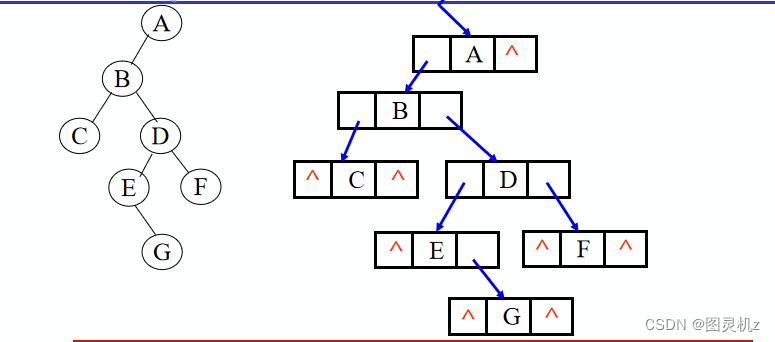
typedef struct BiNode{
   TElemType   data;
   struct  BiNode   *lchild,*rchild; //左右孩子指针
}BiNode,*BiTree; 

在n个结点的二叉链表中，有n+1个空指针域

分析：必有2n个链域。除根结点外，每个结点有且仅有一个双亲，所以只会有n－1个结点的链域存放指针，指向非空孩子结点。

空指针数目=2n-(n-1)=n+1

三叉链表：有双亲和左右孩子指针

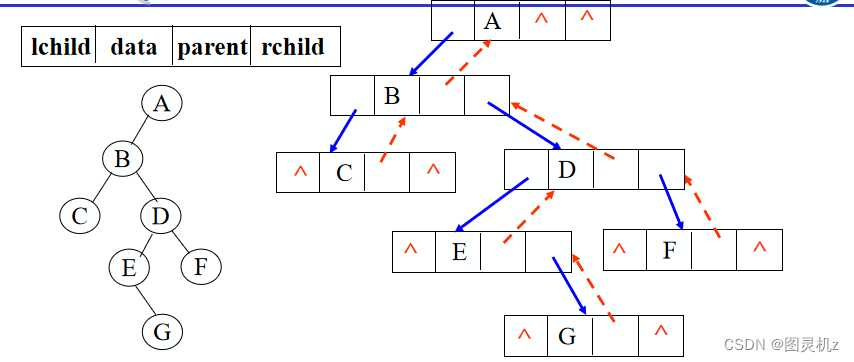
typedef struct TriTNode{
    TelemType data;
    struct TriTNode *lchild,*parent,*rchild;
}TriTNode,*TriTree;

4.3、遍历二叉树

遍历定义——指按某条搜索路线遍访每个结点且不重复（又称周游）。

遍历用途——它是树结构插入、删除、修改、查找和排序运算的前提，是二叉树一切运算的基础和核心

遍历规则

先左后右

DLR（先序） LDR（中序） LRD（后序）（√）

DRL RDL RLD(×)

用二叉树表示算术表达式

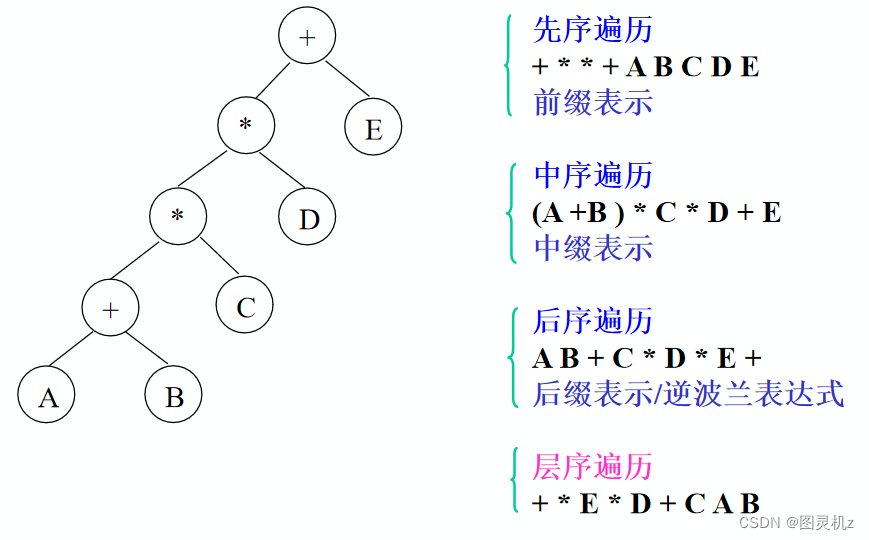
遍历的算法实现——先序遍历

若二叉树为空，则空操作
否则

访问根结点 (D)

先序遍历左子树 (L)

先序遍历右子树 ®

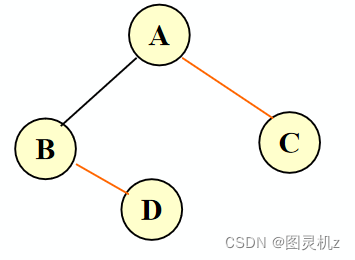
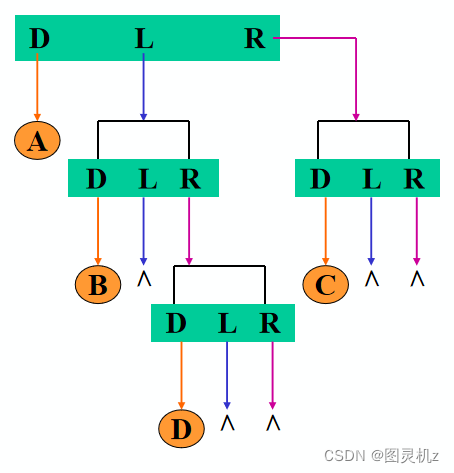
先序遍历序列：A B D C

遍历的算法实现－－用递归形式格外简单！

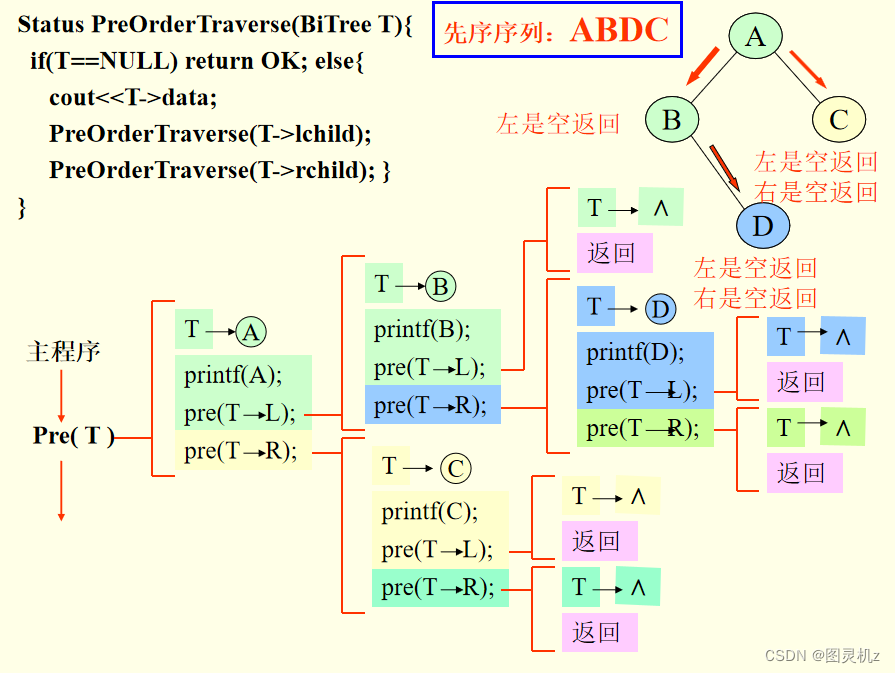
先序遍历算法

Status PreOrderTraverse(BiTree T){
  if(T==NULL) return OK; //空二叉树
  else{    
     cout<<T->data; //访问根结点
     PreOrderTraverse(T->lchild); //递归遍历左子树
     PreOrderTraverse(T->rchild); //递归遍历右子树
    }
}

遍历的算法实现－中序遍历

若二叉树为空，则空操作
否则:

中序遍历左子树 (L)

访问根结点 (D)

中序遍历右子树 ®

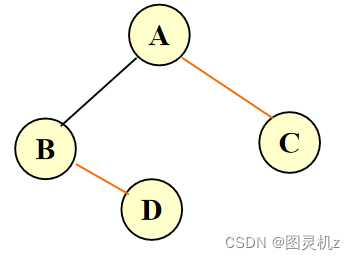
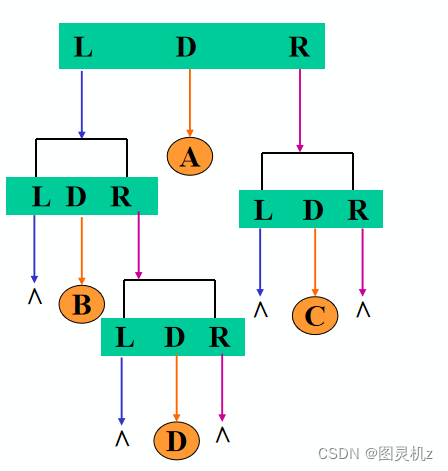
中序遍历序列：B D A C

中序遍历算法

Status InOrderTraverse(BiTree T){
  if(T==NULL) return OK; //空二叉树
  else{    
     InOrderTraverse(T->lchild); //递归遍历左子树
  cout<<T->data; //访问根结点
     InOrderTraverse(T->rchild); //递归遍历右子树
    }
}

遍历的算法实现－后序遍历

若二叉树为空，则空操作
否则

后序遍历左子树 (L)

后序遍历右子树 ®

访问根结点 (D)

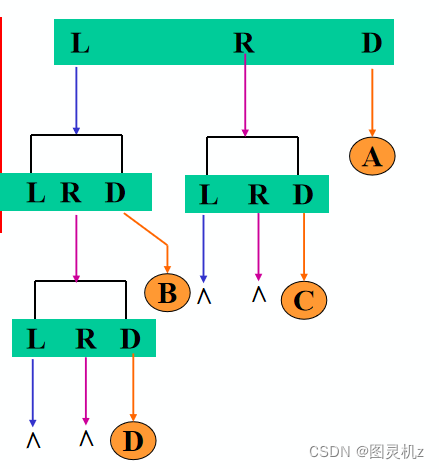
后序遍历序列： D B C A

Status PostOrderTraverse(BiTree T){
  if(T==NULL) return OK; //空二叉树
  else{    
     PostOrderTraverse(T->lchild); //递归遍历左子树
     PostOrderTraverse(T->rchild); //递归遍历右子树
     cout<<T->data; //访问根结点
    }
}

遍历算法的分析

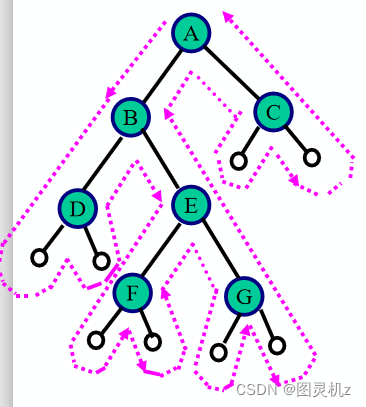
如果去掉输出语句，从递归的角度看，三种算法是完全相同的，或说这三种算法的访问路径是相同的，只是访问结点的时机不同。

从虚线的出发点到终点的路径上，每个结点经过3次。

第1次经过时访问＝先序遍历
第2次经过时访问＝中序遍历
第3次经过时访问＝后序遍历

时间效率:O(n) //每个结点只访问一次
空间效率:O(n) //栈占用的最大辅助空间

二叉树的建立

按先序遍历序列建立二叉树的二叉链表

例：已知先序序列为： A B C   D E  G   F   

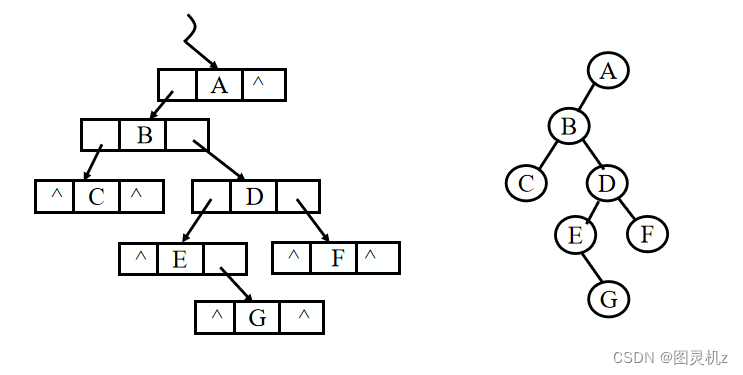
常识：

• 若二叉树中各结点的值均不相同，则：
  由二叉树的前序序列+中序序列，或由其后序序列+中序序列均能唯一地确定一棵二叉树，
  但由前序序列+后序序列却不一定能唯一地确定一棵二叉树。
• 后序遍历，根节点必须在后序序列的尾部
• 前序遍历，根节点必须在前序序列的头部

练习：

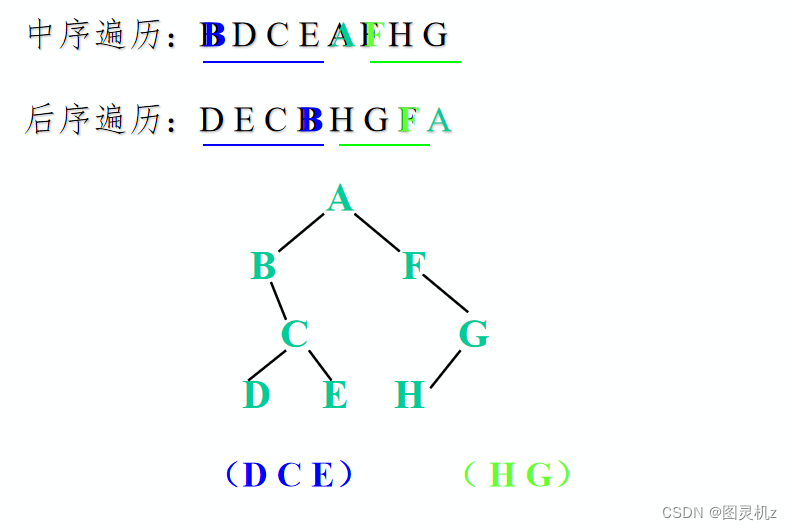
已知一棵二叉树的中序序列和后序序列分别是BDCEAFHG 和 DECBHGFA，请画出这棵二叉树。

①由后序遍历特征，根结点必在后序序列尾部（A）；
②由中序遍历特征，根结点必在其中间，而且其左部必全部是左子树子孙（BDCE），其右部必全部是右子树子孙（FHG）；
③继而，根据后序中的DECB子树可确定B为A的左孩子，根据HGF子串可确定F为A的右孩子；以此类推。

二叉树遍历算法的应用

• 计算二叉树结点总数
• 计算二叉树叶子总数
• 计算二叉树高度

4.4、树和森林

树的存储结构
－双亲表示法
－孩子表示法
－双亲孩子表示法
－孩子兄弟表示法

树的存储结构－双亲表示法

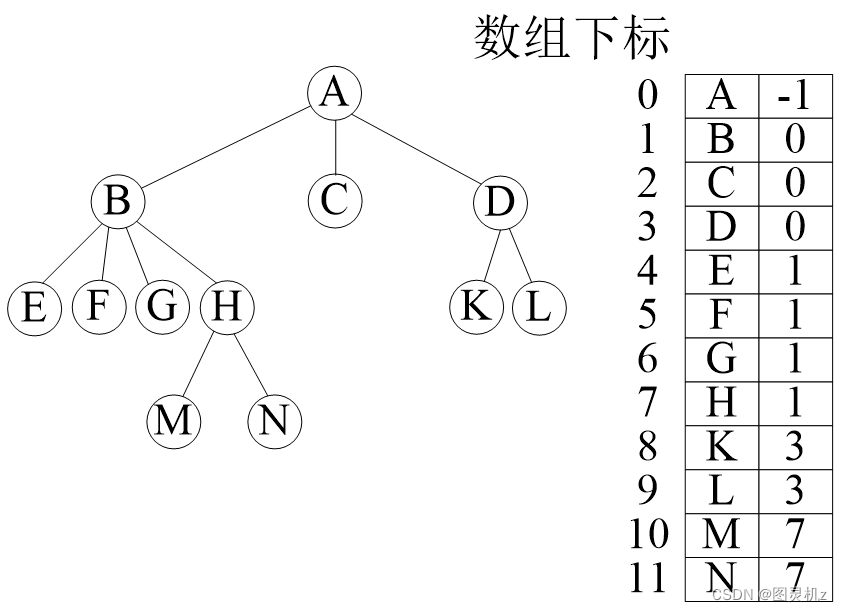
树的存储结构－孩子表示法

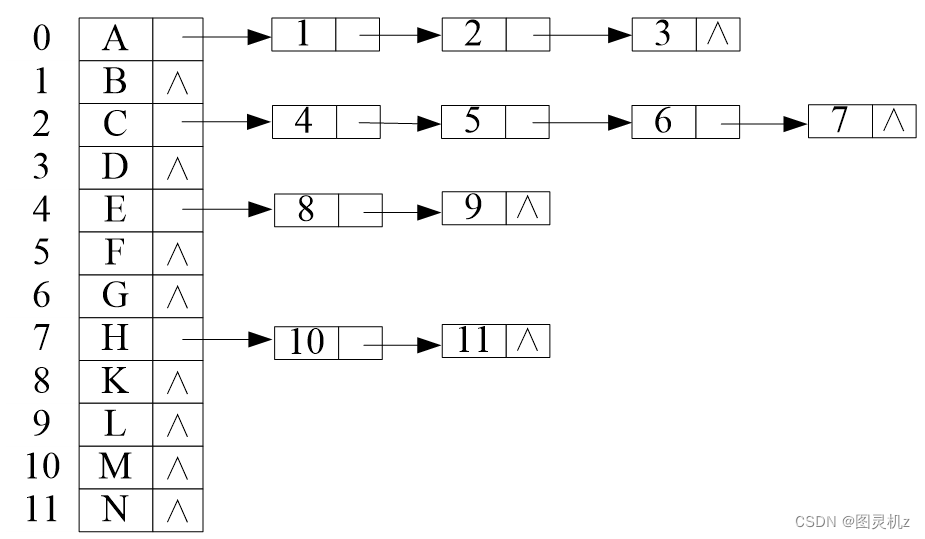
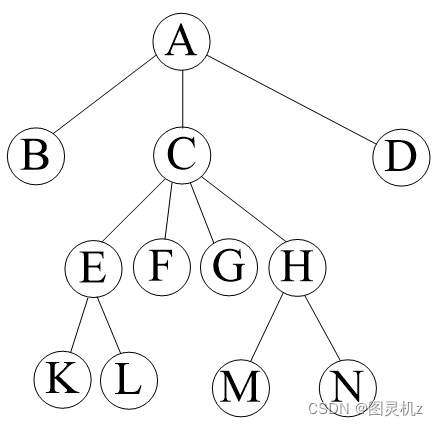
树的存储结构－双亲孩子表示法

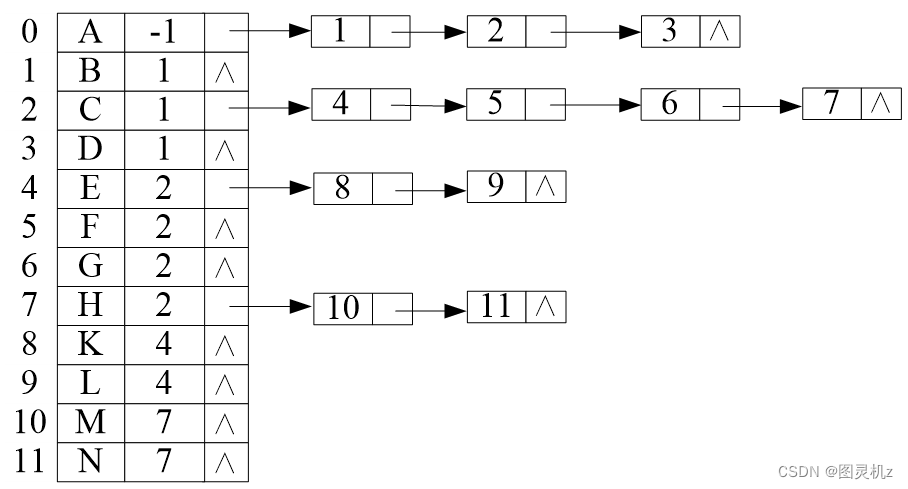
树的存储结构－孩子兄弟表示法

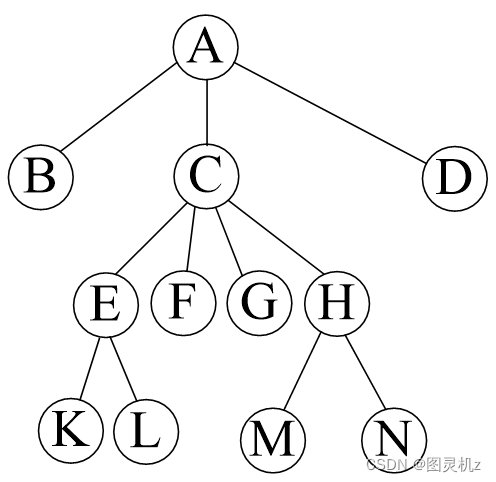
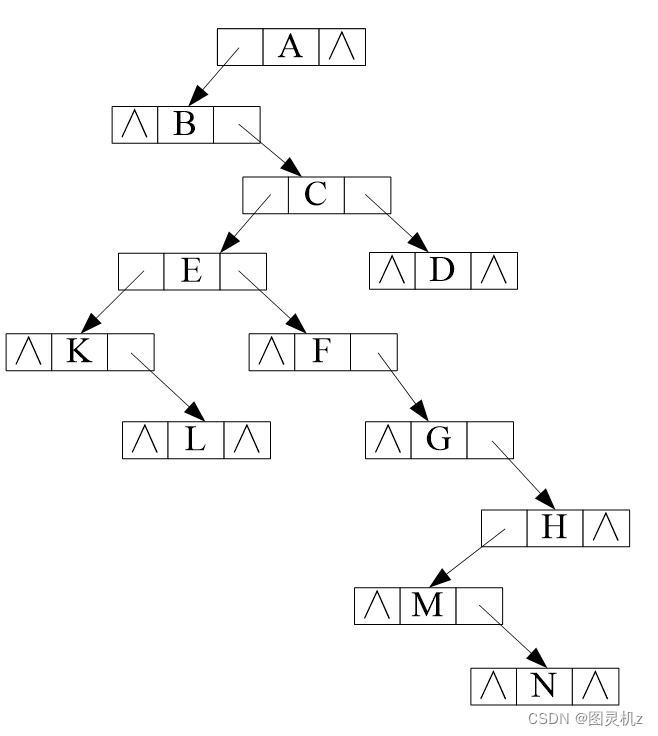
森林的存储结构
－双亲表示法
－孩子表示法
－孩子兄弟表示法

树、森林和二叉树的相互转换

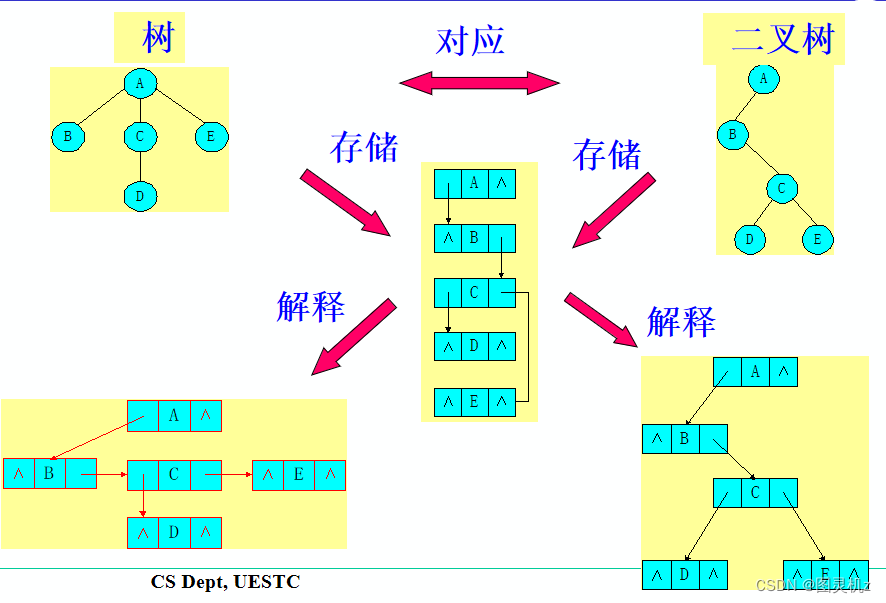
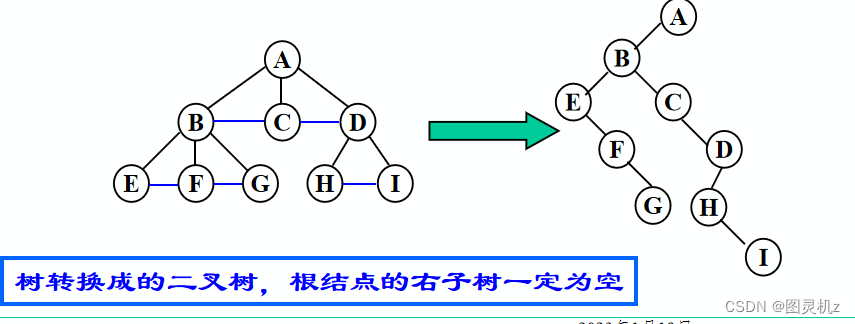
树→二叉树

• 加线：将兄弟结点用线相连
• 抹线：保留双亲与最左边孩子的连线，去掉双亲和其他孩子的连线
• 旋转：将经过加线和去线以后的结果，进行旋转处理得到转换后的二叉树

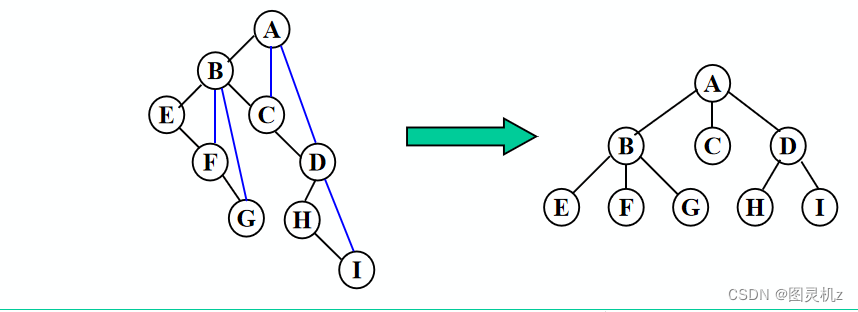
二叉树→树

• 加线：将结点和其左孩子结点的右孩子以及右孩子的右孩子加线相连
• 抹线：去掉结点和右孩子的连线
• 旋转：将加线、去线后的结果，进行旋转处理，就得到转换后的树

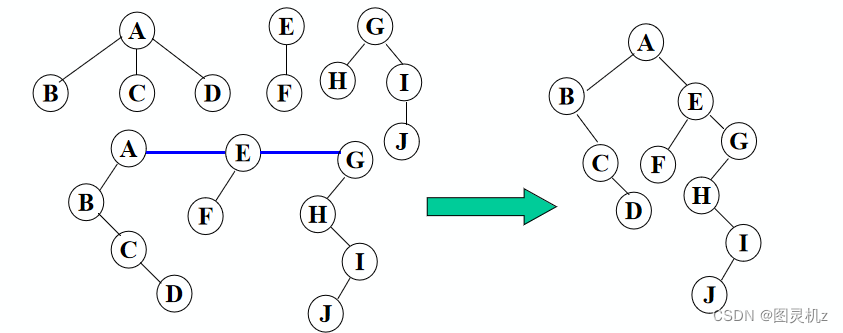
森林→二叉树

• 将每棵树分别转换成二叉树
• 将每棵树的根结点用线相连
• 以第一棵树根结点为二叉树的根，再以根结点为轴心，顺时针旋转，构成二叉树型结构

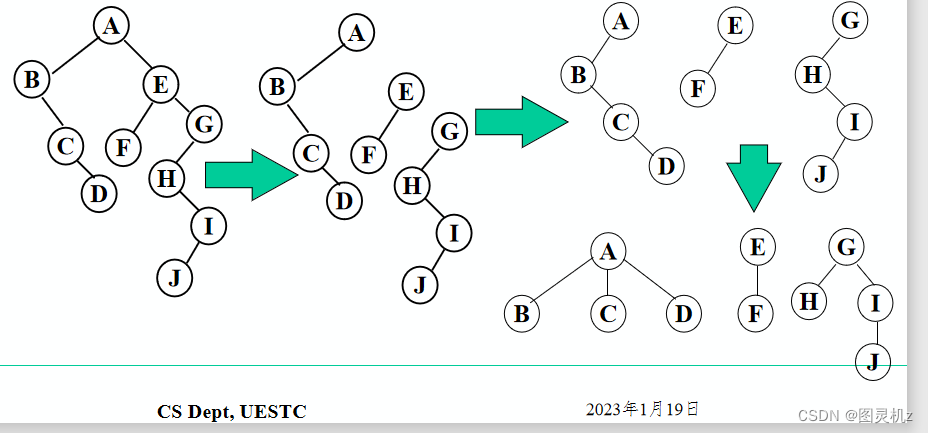
二叉树→森林

• 抹线：将二叉树中根结点与其右孩子连线，及沿右分支搜索到的所有右孩子间连线
• 全部抹掉，使之变成孤立的二叉树
• 还原：将孤立的二叉树还原成树

树的遍历

按一定规律走遍树的各个顶点，且使每一顶点仅被访问一次，即找一个完整而有规律的走法，以得到树中所有结点的一个线性排列
遍历方法
先根（序）遍历：先访问树的根结点，然后依次先根遍历根的每棵子树
后根（序）遍历：先依次后根遍历每棵子树，然后访问根结点
按层次遍历：先访问第一层上的结点，然后依次遍历第二层，……第n层的结点

”树“非同二叉树它没有中序遍历

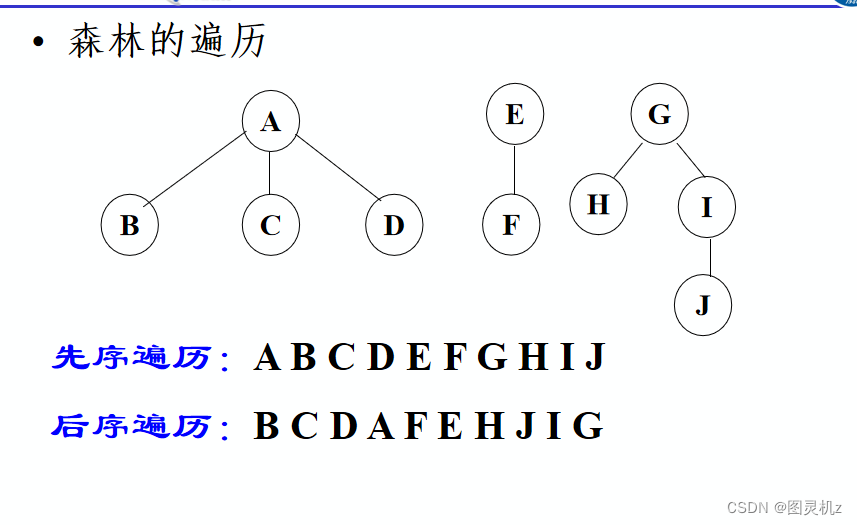
森林的遍历

• 先序遍历
  • 访问森林中第一棵树的根结点
  • 先序遍历第一树中根结点的子树森林
  • 先序遍历除去第一棵树之后剩余的森林
• 后序遍历
  • 后序遍历森林中第一棵树的根结点的子树森林
  • 访问第一棵树的根结点
  • 后序遍历除去第一棵树之后剩余的森林

4.5、二叉树的应用

4.5.1二叉排序树

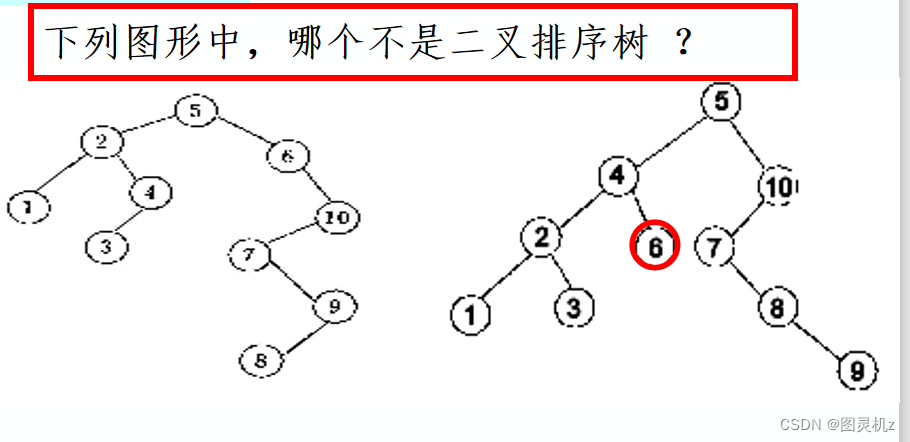
二叉排序树或是空树，或是满足如下性质的二叉树：
(1)若其左子树非空，则左子树上所有结点的值均小于根结点的值；
(2)若其右子树非空，则右子树上所有结点的值均大于等于根结点的值；
(3)其左右子树本身又各是一棵二叉排序树

中序遍历二叉排序树后的结果有什么规律？

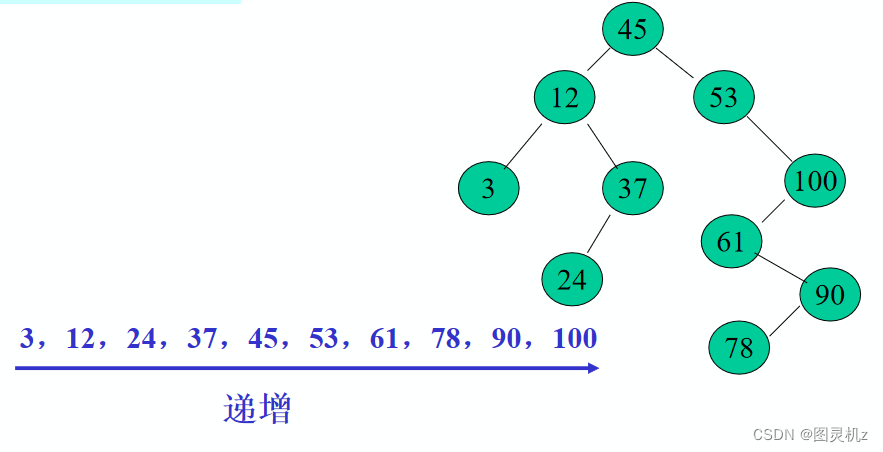
得到一个关键字的递增有序序列

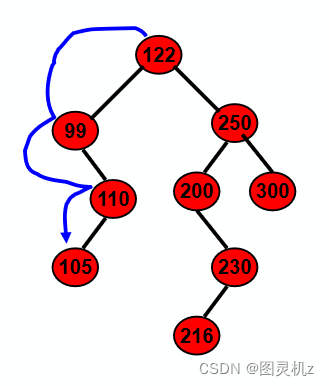
二叉排序树的操作－查找

若查找的关键字等于根结点，成功
否则
　若小于根结点，查其左子树
　若大于根结点，查其右子树
在左右子树上的操作类似

算法描述

BSTree SearchBST(BSTree T, KeyType key) {
   if((!T) || key==T->data.key) return T;       	 
   else if (key<T->data.key)  return SearchBST(T->lchild,key);	//在左子树中继续查找
   else return SearchBST(T->rchild,key);    		   		//在右子树中继续查找
} // SearchBST

二叉排序树的操作－插入

若二叉排序树为空，则插入结点应为根结点
否则，继续在其左、右子树上查找

• 树中已有，不再插入
• 树中没有，查找直至某个结点的左子树或右子树为空为止，则插入结点应为该结点的左孩子或右孩子

插入的元素一定在叶结点上

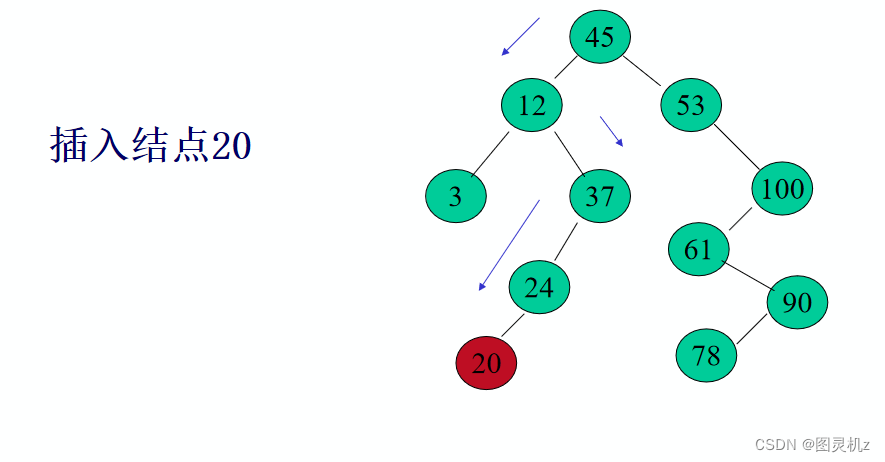
二叉排序树的操作-生成

从空树出发，经过一系列的查找、插入操作之后，可生成一棵二叉排序树

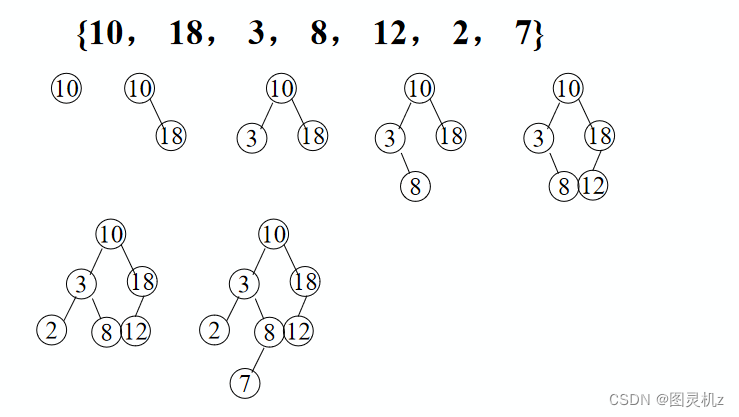
不同插入次序的序列生成不同形态的二叉排序树

• 将因删除结点而断开的二叉链表重新链接起来

• 防止重新链接后树的高度增加

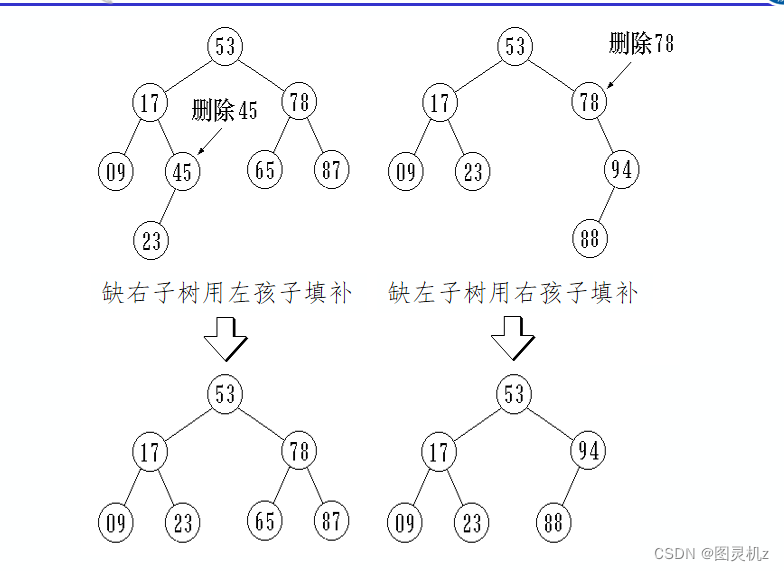
• 删除叶结点，只需将其双亲结点指向它的指针清零，再释放它即可。

• 被删结点缺右子树，可以拿它的左孩子结点顶替它的位置，再释放它。

• 被删结点缺左子树，可以拿它的右孩子结点顶替它的位置，再释放它。

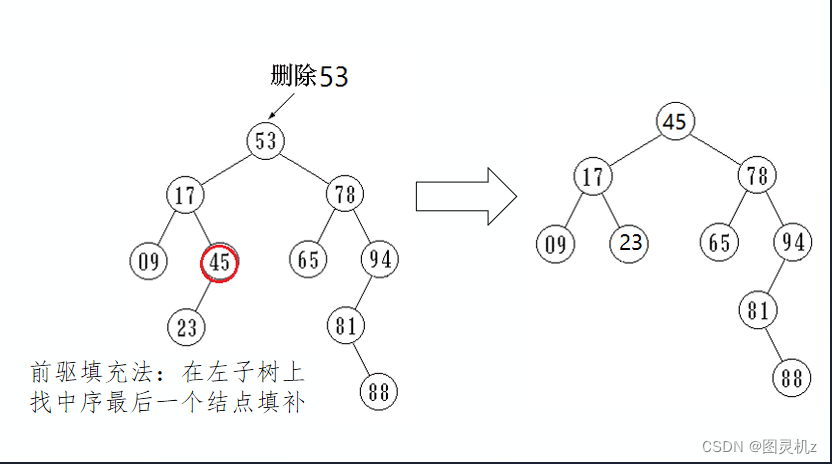
• 被删结点左、右子树都存在，可以在它的右子树中寻找中序下的第一个结点(后继填

• 充法),或是在它的左子树中寻找中序下的最后一个结点(前驱填充法)，用它的值填补

• 到被删结点中，再来处理这个结点的删除问题。

内容未完待续，后续再次更新