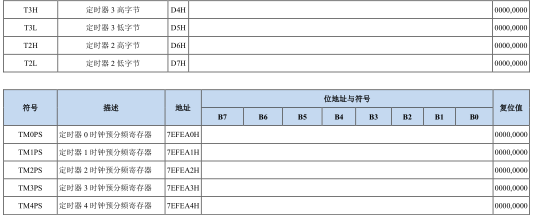
1. 概述
在推荐系统中,通常有多个业务目标需要同时优化,常见的指标包括点击率CTR、转化率CVR、 GMV、浏览深度和品类丰富度等。为了能平衡最终的多个目标,需要对多个目标建模,多目标建模的常用方法主要可以分为:
- 多模型的融合
- 多任务学习
- 底层共享表示的优化
- 任务序列依赖关系建模
多模型的融合是根据不同的指标训练不同的模型,最终对多个模型的结果做融合;多任务学习是目前处理多目标建模使用较多的方法,相较于多模型的融合,多任务学习能做到端到端的学习,同时能够节约建模的时间,因为多个模型可以同时建模。在多任务学习中,又可以细分成底层共享表示的优化和任务序列依赖关键的建模。在底层共享表示的优化中,以MMoE(Multi-gate Mixture-of-Experts)[1]和PLE(Progressive Layered Extraction)[2]两种网络结构较为常用。在任务序列依赖关系建模中,以阿里的ESMM[3]较为典型。
在多目标的建模过程中,如果不同的学习任务之间较为相关时,多个任务之间可以共享一部分的信息,这样最终能够提升整体的模型学习效果。但是如果多个任务之间的相关性并不强,或者说多个任务之间存在某种冲突,这样通过部分的共享就会起到事与愿违的效果,这便是通常所说的在多任务建模中出现的负迁移(negative transfer)现象,即在相关性不强或者无相关性的多任务环境下进行信息共享,最终影响整体的网络效果;另一方面,在多任务建模过程中,还存在一种被称为跷跷板现象(seesaw phenomenon),简单来说就是在对多个目标进行优化的过程中,一个任务指标的提升伴随着另外一些任务指标的下降。出现这种现象的主要原因是多个任务之间出现较多的共享。因此,很多的改进算法都在致力于解决这两个问题。
2. 多目标建模的常用方法
2.1.多模型的融合
多模型的融合是指根据不同的任务单独训练不同的模型,最终根据最终的目标将各模型的结果相加或者相乘后进行融合排序。以CTR和CVR为例,最终的目标通常是CTCVR,因此,可以分别训练一个CTR模型和CVR模型,如下图所示:

通常在实际的任务中会根据不同任务的重要性,对该任务赋予不同的权重。这种方案最主要的优点是相对较为简单,每次单独训练一个模型,只需要调优该模型,不需要考虑其它目标。缺点也是很明显的,主要有如下的几个方面:
- 多个模型结果的融合,这里面涉及到超参数的选择,通常可以采取grid search的方案确定超参;
- 每次调优一个模型,而不更新组合并不一定会带来最终效果的提升;
- 没有考虑两个数据之间的关系,如上述的CTR与CVR之间存在顺序的关系;
2.2. 多任务学习
对于多模型融合存在的问题,通过多任务学习能够在一定程度上解决这些问题,首先,在多任务学习中,由于将多个模型合并成一个模型,这样能够减少维护成本及减少资源;对于数据较为稀疏的任务,通过多任务学习的方式,能够提高模型的效果;
2.2.1. 底层共享表示的优化
在底层共享表示优化中,目前业界主流的多目标建模的网络结构是MMoE[1]和PLE[2]两种,其中MMoE的网络结构如下图c所示:

在上图a中是Shared-Bottom model,任务A和任务B共享部分的网络结构,假设这部分的共享网络结构由 f ( x ) f\left ( x \right ) f(x)表示, h A ( f ( x ) ) h^A\left ( f\left ( x \right ) \right ) hA(f(x))表示的是任务A的输出, h B ( f ( x ) ) h^B\left ( f\left ( x \right ) \right ) hB(f(x))表示的是任务B的输出,综上,Shared-Bottom Model可由下式表示:
y k = h k ( f ( x ) ) y_k=h^k\left ( f\left ( x \right ) \right ) yk=hk(f(x))
通过在底层共享网络,能够起到互相补充学习的作用,上层的任务之间相关性越高,对于模型的学习也会越充分,但是,如果上层的任务之间的相关性很差,这种情况对于最终的效果却是起到了抑制的作用,即上面提到的负迁移现象,这也是多任务学习难以训练的一个原因。在很多的图像相关的任务中,就存在这样的结构,以人脸检测任务为例,在人脸检测任务重包括了三个方面的目标,分别为face classification,bounding box regression和facial landmark localization,这三个任务可以共享底层的CNN网络,以MTCNN[4]模型为例,其中的O-Net的网络结构如下图所示:

最终的损失函数为:
m i n ∑ i = 1 N ∑ j ∈ { d e t , b o x , l a n d m a r k } α j β i j L i j min\; \sum_{i=1}^{N}\sum_{j\in \left \{ det,box,landmark \right \}}\alpha _j\beta _i^jL_i^j mini=1∑Nj∈{det,box,landmark}∑αjβijLij
其中, α j \alpha _j αj和 β i j \beta _i^j βij是两个超参,这两个超参在参考[4]中是根据经验值确定的, L i j L_i^j Lij表示的是第 j j j个任务的损失函数。
上图b中是One-gate MoE model,相比于Shared-Bottom model,有两点优化,第一,引入多个Shared Bottom组成MoE结构;第二,引入门控网络Gate函数。One-gate MoE Model可由下式表示:
y k = h k ( ∑ i = 1 n g ( x ) i f i ( x ) ) y_k=h^k\left ( \sum_{i=1}^{n}g\left ( x \right )_if_i\left ( x \right ) \right ) yk=hk(i=1∑ng(x)ifi(x))
在底层共享网络的基础上,引入了多个Shared Bottom,对于不相关的任务联合学习效果不佳问题,能够通过类似集成方法的方式针对不同上层任务选择不同的底层共享网络,使得不同任务具有不同的底层网络。但是在One-gate的模型下,仍然存在一些问题,如多个任务对于底层的分布是一致的。
上图c中是Multi-gate MoE model,MMoE是在One-gate MoE Model的基础上,针对每一个任务独享一个门控网络,Multi-gate MoE Model可由下式表示:
y k = h k ( ∑ i = 1 n g k ( x ) i f i ( x ) ) y_k=h^k\left ( \sum_{i=1}^{n}g^k\left ( x \right )_if_i\left ( x \right ) \right ) yk=hk(i=1∑ngk(x)ifi(x))
MMoE针对每个任务有单独的门控网络 g k ( x ) i g^k\left ( x \right )_i gk(x)i,同时在底部共享几个专家网络,通过不同的门控网络去控制专家网络对于不同任务的权重贡献,这样不同的任务对于多个专家的分布是不同的,能够有效对任务之间的联系进行建模。然而,在MMoE模型中,只是强调对于上层任务的共性构建底层专家,对于上层任务的差异却没有区别对待,CGC便是基于这样的目的被提出的模型,CGC模型的结构如下图所示:

在CGC的网络结构中,其底层网络包括了shared experts和task-specific expert两个部分,且每一个expert部分都是由多个expert组成,上层针对每一个任务都有一个门控网络,且门控网络的输入是共享的experts和该任务对应的experts。由此可见,在CGC网络中,既包含了task-specific网络针对特定任务独有的信息,也包含了shared网络共享的信息。为了与MMoE中的表达式一致,修改在参考[2]中的表达式,因此CGC网络可以表示为:
y k = h k ( ∑ i = 1 m k + m s g k ( x ) i f i ( x ) ) y_k=h^k\left ( \sum_{i=1}^{m_k+m_s}g^k\left ( x \right )_if_i\left ( x \right ) \right ) yk=hk(i=1∑mk+msgk(x)ifi(x))
其中,对于专家输出 f i ( x ) f_i\left ( x \right ) fi(x)中,包含了两个部分,一个是特定任务对应的专家,另一部分是共享的专家。为了能够得到更具有泛化能力的网络,可以将上述网络构建得更深,这便有了PLE结构,PLE是在CGC网络结构的基础上,由single-level衍生为multi-level。具体的PLE网络结构如下图所示:

除了第一个Extraction Network的输入是原始的Input,其余的Extraction Network的输入是上一个Extraction Network的输出,即包含两个大的部分,即特定任务对应的专家网络输出,如上图中的Experts A和Experts B的输出,另外一个是共享专家网络的输出,如上图中的Experts Shared的输出。在多任务重,其损失函数为各任务损失的加权求和,即为:
L k ( θ 1 , ⋯ , θ K , θ s ) = ∑ k = 1 K ω k L k ( θ k , θ s ) L_k\left ( \theta _1,\cdots ,\theta _K,\theta _s \right )=\sum_{k=1}^{K}\omega _kL_k\left ( \theta _k,\theta _s \right ) Lk(θ1,⋯,θK,θs)=k=1∑KωkLk(θk,θs)
其中, ω k \omega _k ωk为第 k k k个任务的权重,具体对于 ω k \omega _k ωk的设置可以见参考[2]。
2.2.2. 任务序列依赖关系建模
对于CTR,CVR这样的多任务情况下,两个任务之间是存在相互依赖关系的,假设 x \mathbf{x} x表示的是一条曝光样本, y ∈ { 0 , 1 } y\in \left\{ 0,1\right\} y∈{0,1}表示的是该曝光样本是否被点击, z ∈ { 0 , 1 } z\in \left\{ 0,1\right\} z∈{0,1}表示的是该样本在曝光点击后是否有转化,对点击率(CTR)建模是预估点击率: p C T R = p ( y = 1 ∣ x ) pCTR=p\left ( y=1\mid \mathbf{x} \right ) pCTR=p(y=1∣x),对CVR建模是预估转化率: p C V R = p ( z = 1 ∣ y = 1 , x ) pCVR=p\left ( z=1\mid y=1,\mathbf{x} \right ) pCVR=p(z=1∣y=1,x)。然而上述的诸如MMoE或者PLE的模型中并未考虑任务之间的序列依赖关系。对于CVR的建模,在训练时只能利用点击后的样本,而预测时,是在整个样本空间,这样导致训练和预测样本分布不一致,即样本选择性偏差。同时点击样本只占整个样本空间的很小比例,存在样本稀疏性问题。
在CTR,CVR这个多任务场景下,ESMM(Entire space multi-task model)[3]模型就是为解决上述两个问题而提出,在ESMM模型的建模过程中引入两个辅助任务,即:CTR建模和CTCVR建模。对于点击转化率(CTCVR): p C T C V R = p ( y = 1 , z = 1 ∣ x ) pCTCVR=p\left ( y=1,z=1\mid \mathbf{x} \right ) pCTCVR=p(y=1,z=1∣x),pCTR,pCVR和pCTCVR三者之间的关系为:
p ( z = 1 ∣ y = 1 , x ) = p ( y = 1 , z = 1 ∣ x ) p ( y = 1 ∣ x ) p\left ( z=1\mid y=1,\mathbf{x} \right )=\frac{p\left ( y=1,z=1\mid \mathbf{x} \right )}{p\left ( y=1\mid \mathbf{x} \right )} p(z=1∣y=1,x)=p(y=1∣x)p(y=1,z=1∣x)
ESMM的网络结构如下图所示:

在ESMM模型结构中,有两个特点,第一,在ESMM结构中包含了两个塔,左侧是一个CVR任务的塔,右侧是一个CTR任务的塔,因为不直接对CVR建模,因此输入空间师整个曝光样本空间;第二,在两个塔的底层Embedding层是参数共享的,这样能缓解传统的CVR建模过程中面临的数据稀疏问题。ESMM的损失函数为:
L ( θ c v r , θ c t r ) = ∑ i = 1 N l ( y i , f ( x i ; θ c t r ) ) + ∑ i = 1 N l ( y i & z i , f ( x i ; θ c t r ) × f ( x i ; θ c v r ) ) \begin{align*} L\left ( \theta _{cvr},\theta _{ctr} \right ) &= \sum_{i=1}^{N}l\left ( y_i,f\left ( \mathbf{x}_i;\theta _{ctr} \right ) \right )\\ &+ \sum_{i=1}^{N}l\left ( y_i\&z_i,f\left ( \mathbf{x}_i;\theta _{ctr} \right )\times f\left ( \mathbf{x}_i;\theta _{cvr} \right ) \right ) \end{align*} L(θcvr,θctr)=i=1∑Nl(yi,f(xi;θctr))+i=1∑Nl(yi&zi,f(xi;θctr)×f(xi;θcvr))
其中, θ c v r \theta _{cvr} θcvr表示的是CVR塔中的参数, θ c t r \theta _{ctr} θctr表示的是CTR塔中的参数, y i y_i yi表示的是样本 x i \mathbf{x}_i xi在CTR任务上的label, z i z_i zi表示的是样本 x i \mathbf{x}_i xi在CVR任务上的label, f ( x i ; θ c t r ) f\left ( \mathbf{x}_i;\theta _{ctr} \right ) f(xi;θctr)表示的样本 x i \mathbf{x}_i xi在CTR塔中的结果, f ( x i ; θ c v r ) f\left ( \mathbf{x}_i;\theta _{cvr} \right ) f(xi;θcvr)表示的是样本 x i \mathbf{x}_i xi在CVR塔中的结果。
3. 总结
多目标建模已经成为当前推荐系统中的标配,在多目标建模过程中,需要考虑多个目标之间的相互关系,以选择合适的多目标建模方法,同时,在多目标的损失函数的设计上,也存在很多的优化方案,需要根据具体的应用场景选择合适的损失函数,以达到对具体任务的优化。
参考文献
[1] Ma J, Zhao Z, Yi X, et al. Modeling task relationships in multi-task learning with multi-gate mixture-of-experts[C]//Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. 2018: 1930-1939.
[2] Tang H, Liu J, Zhao M, et al. Progressive layered extraction (ple): A novel multi-task learning (mtl) model for personalized recommendations[C]//Fourteenth ACM Conference on Recommender Systems. 2020: 269-278.
[3] Ma X, Zhao L, Huang G, et al. Entire space multi-task model: An effective approach for estimating post-click conversion rate[C]//The 41st International ACM SIGIR Conference on Research & Development in Information Retrieval. 2018: 1137-1140.
[4] Zhang K, Zhang Z, Li Z, et al. Joint face detection and alignment using multitask cascaded convolutional networks[J]. IEEE signal processing letters, 2016, 23(10): 1499-1503.
[5] 网易严选跨域多目标算法演进