机器学习入门
机器学习中需要理论性的知识,如数学知识为微积分(求导过程,线性回归的梯度下降法),线性代数(多元线性回归,高纬度的数据,矩阵等),概率论(贝叶斯算法),统计学(贯穿整个学习过程),算法根据数学基础一步步的推导出来的。
需要编程语言把学到的知识应用到实践中,python语言的语法比较简单,第三方库比较丰富,可以在各行各业发挥作用,很方便的对数据进行分析和处理,进行模型的训练。
机器学习算法的学习主线为K近邻算法、线性回归算法、梯度下降法策略、逻辑回归算法、决策树算法、集成算法于随机森林、支持向量机(SVM)、贝叶斯算法、聚类算法、降维算法等。算法间的关联度比较低, 不要因为一个算法的不理解而放弃整个阶段的学习。
算法学习的四大步骤
- 第一步:掌握经典的算法(推导的原理、代码的实现)
- 第二步:读懂算法代码,知道算法是怎么由数学实现的,通过代码实现推导的过程
- 第三步:写出经典的算法。自己尝试去模仿写一下。
- 第四步:改算法。通常不需要我们从0到1去构建算法,看懂别人的算法原理,基于别人的文献去改一些算法。
发展方向
1.python数据分析师
2.AI基础
人工智能的分支
人工智能的应用已经渗透到我们的生活当中,现在仍处于弱人工智能的阶段(基于数据去做决策的,如AI推荐系统,AI智能回复等,并不是人工智能的思考能力;强人工智能是指机器具备了人的思考能力),机器学习是AI方向的基础。人工智能会替代一些重复性的劳动工作,如高铁站的检票员,银行的柜员等。
1950年初,人工智能(Artifical Intelligence)已经出现,应用在有钱人的娱乐世界,下棋的领域,如五子棋,飞旗,国际象棋,围棋等。到1980年代的时候出现了机器学习(Machine Learning),西方互联网发展的比较迅速,作为人工职能的分支,机器学习实现了自动识别垃圾邮件。到2010年,随着时代的发展,业务量增多,如上班的人脸打卡系统,购物网站的智能客服等等,出现了深度学习(Deep Learning)用来解决图像识别的问题。
人工智能、机器学习、深度学习的关系
人工智能是一个更加广泛的词语,机器学习是实现人工智能的一个途径,深度学习是机器学习的一个分支,社会需求的发展导致深度学习(神经网络算法)慢慢发展壮大,可以解决实际的需求。
人工智能必备三要素
数据:弱人工智能,需要数据(经验)来判断,如等公交时对公交车到达时间的判断。对于机器而言,也需要大量的数据做支撑。
算法:合适的算法
计算力:计算的能力,处理大量的数据。可以放到服务器上运行真实的数据和代码。
CPU,办公使用,商务本,对文件进行读写操作,轻薄,方便携带,运行的数据量小。
GPU,游戏本,对大量数据进行计算和处理,笨重,运行的数据量大。
服务器,云服务器和部署的服务器,数据量比较大。
机器学习应用
机器学习是从数据中自动分析获取模型,并利用模型对未知数据进行预测。应用的方面:图像识别、推荐系统、自动驾驶。
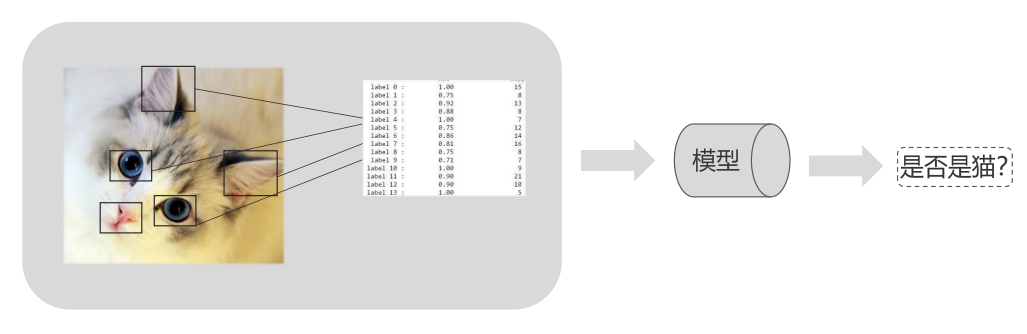
图像识别
小孩看到小猫咪2-3次,就可以分辨出猫和其他动物,机器则需要大量的算法去训练,才可以识别。人可以快速的去学习,去识别,人的学习能力比算法要好很多。机器去学习的时候,需要提取出来猫的特征,比如耳朵尖尖的,眼睛圆圆的,嘴巴鼻子等。然后对特征进行归纳,机器根据特征来判断是不是猫咪,根据特征进行分类,建立模型,当有新的图片输入,机器就利用建立的模型来判断是否是猫咪。
图像识别其实是把图像数据化的过程,特征值需要不停的调试,筛选,核实,检验等。
推荐系统
推荐系统在生活中无处不在,打开一个软件就会出现被推荐的现象,是非常成功的商业模式,可以根据我们浏览过的数据、加购的数据、购买的数据以及其他的数据,来推荐给用户所需要的产品。每个人打开应用软件显示的内容是不一样的,可以说是千人千面。
比如在某宝(某东、某团)上买了一款手机,会给你推荐跟手机相关联的产品,比如充电器,手机壳,钢化膜等等跟产品相关的其他产品,使用关联算法,促进你的消费。如沃尔玛超市的线下推荐系统,根据女孩买纸巾的习惯,判断女孩是否怀孕,从而推荐婴幼儿产品。

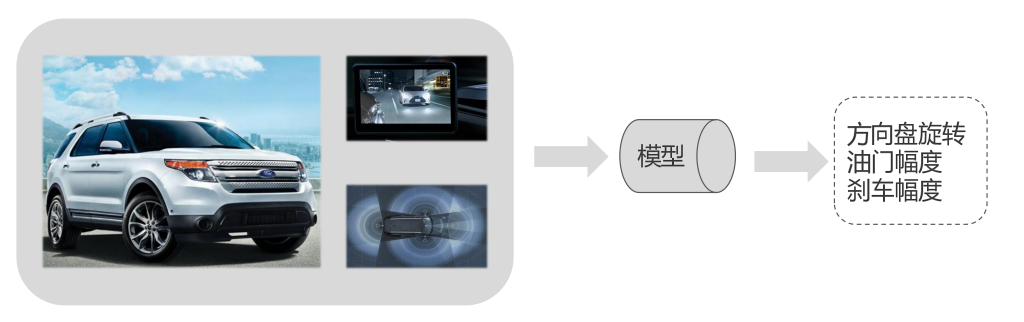
自动驾驶
不论是国内还是国外,目前自动驾驶都已经达到了一定的水平。国内的百度、阿里、腾讯都在研发自动驾驶,目前还是处于辅助的地位,还不能大面积普及,通过车载摄像头和车载雷达搜集周围的信息,导入到模型中,进行训练、决策,对事物进行精准的定位。受限于网络的延迟,还没有被完全的全部应用。
机器学习的流程
历史数据好比人的经验,把数据进行清洗和规范化,并不是每个数据都是有用的,需要提取特征,归纳偏好特征,然后训练出模型,通过模型评估对模型的质量进行检验,模型评估后比较好的才会使用新的数据进行测试,预测相应的结果。不论使用哪个算法,流程是基本一致的。
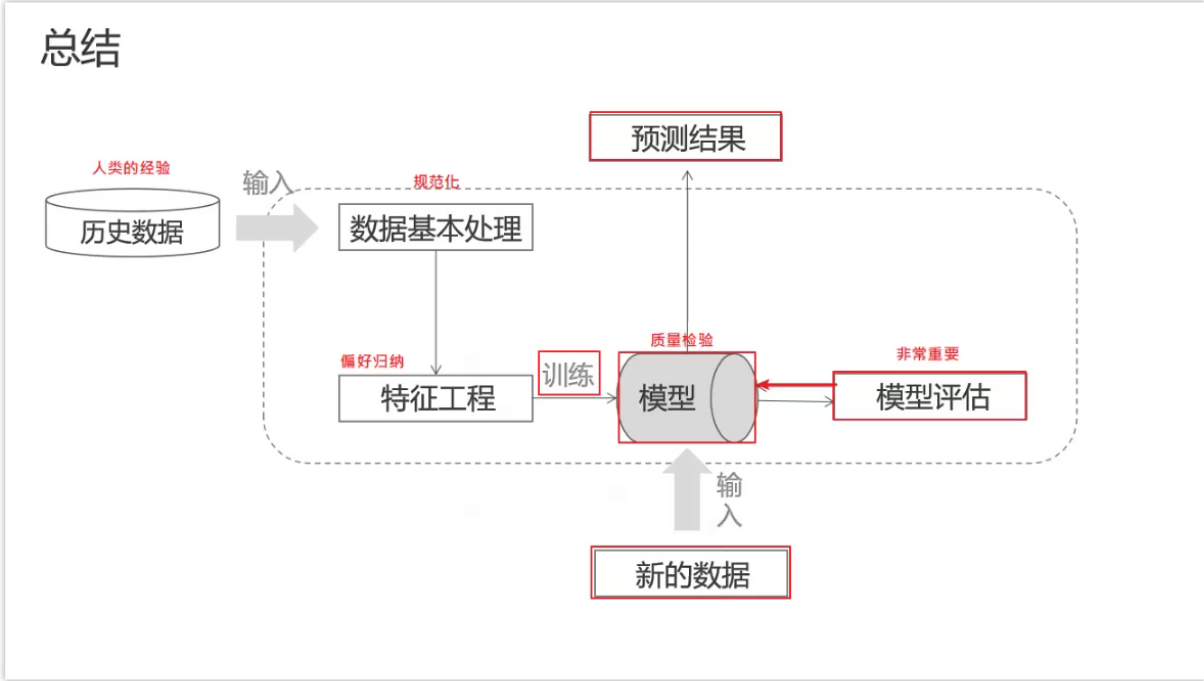
获取数据(历史数据)
- 第一种数据,有目标值,而且是连续的。
如楼房的位置、楼层、大小、朝向等等都会影响到房子的价格,房子的价格是有目标值(标签值)的,根据层数的不同,房子的价格是连续的发生变化。 - 第二种数据,有目标值,是离散的。
动作片和爱情片根据打斗的次数进行区分,类型是有明确的目标的,要么是动作片,要么是爱情片,是离散的数据。
在统计学中,连续的通常是数值,离散的通常是分类。 - 第三种数据,没有明确的目标值,我们可以根据自己想要的样子,把数据聚在一起,化分成想要的类型。
前两种数据,有特征值和目标值,可以通过特征进行推理,有目标值,有评判标准来衡量最终的结果,目标值是有标签的,分为连续和离散的;第三种只有特征值,没有明确的目标值,怎么划分都可以,没有对错之分,只要能划分到一起就可以。
一行数据我们称之为一个样本,如需要分析的每一部电影,一列数据我们称之为一个特征,如每部电影的打斗次数、接吻次数、类型等,构成了历史数据部分。
根据上述的分析,大致分为两类数据类型:第一类为特征值+目标值,目标值来衡量最终的结果,分为连续和离散;第二类只有特征值,没有明确的目标值,怎么划分都可以,没有对错的评判标准。
数据基本处理
数据刚获取下来,往往会有很多问题,我们要对数据进行最基本的处理。
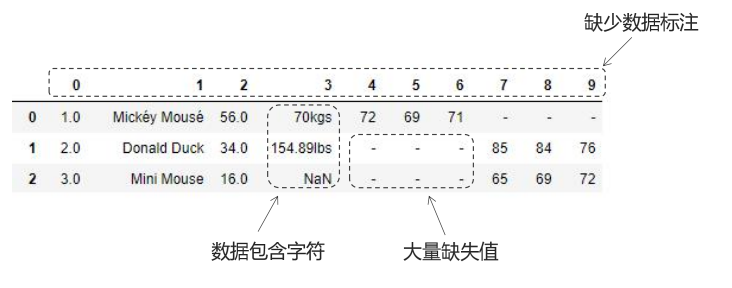
在上图数据中,可以明显的看到NaN、缺失值、单位、每列表示的意义等信息都要进行处理。
对于列名缺少数据标注,不知道每一列数据表示的意义;有大量的缺失值;数据的单位不一致。比如对餐饮的评价,口味是按百分制,服务是按五分制,如果要做综合打分的话,要统一计分方式,需要一个归一化的过程。
坚持的原则是:完全合一
- 完整性:单条数据是否存在空值,统计的字段是否完善。
- 全面性:观察某一列的全部数值,在excel种选中一列可以看到该列的平均值、最大、最小值等,通过观察判断数据是否有问题,如数据差异性大、单位统一、数据定义、单位标识、数据本身等。
- 合法性:数据的类型、内容、大小的合法性。如数据种是否存在非ASCII字符,性别除了男女之外,填写了未知、不明确等,年龄超过150岁或者小于0等,如果不处理这些不合法的数据,就会干扰正常数据。
- 唯一性:数据是否存在重复记录,行数据和列数据均需要是唯一的,如一个人不能重复记录多次,一个人的体重也不能在列指标中重复记录多次等。
特征工程(非常重要)
特征工程是使用专业背景知识和技巧处理数据,使得特征能在机器学习算法上发挥更好的作用的过程,提炼出比较重要的特征,然后再进行处理和择优。
比如生物学的学生学习python和机器学习,需要观察白细胞和红细胞的个数,这时就要区分二者的差别。根据观察,归纳白细胞和红细胞的特征,然后去建立特征。面积大的是白细胞,小的是红细胞;周长大的是白细胞,短的是红细胞;白细胞不圆,红细胞比较圆;圆里面粗糙的是白细胞,平滑的是红细胞。

根据特征进行红白细胞的划分,并不说建立的所有特征都可以拿到算法里去使用的,我们要提取偏好更加优异的特征去训练算法。
特征工程的内容包括如下:
- 特征提取:计算机看不懂分析出来的特征,将文本信息转为计算机可读懂的数字,计算机只能读懂二进制数。适用于分类型、离散型的数据。
- 特征预处理:通过一些转换函数将特征数据转换成更加适合算法模型的特征数据过程。比如同是80分的两个项目,但是总分不一致,一个是满分100,一个满分720,此时要对数据进行归一化及标准化。适用于连续性的数据。
- 特征降维:在某些限定条件下,降低随机变量(特征)个数,得到一组“不相关”主变量的过程。从多变少、从高维变低维、把相关性变为不相关性的过程。
如特征的提取非常的好,数据很完美,则模型建立的很差,最终预测的结果也会非常好;如果特征数据非常差,模型建立的再好,最终得到的结果也不会很差。
模型
模型即为机器学习算法,选择合适的算法,就要了解机器学习算法的分类,根据数据集组成的不同,主要划分为:
监督学习(Supervised learning)
无监督学习(Unsupervised learning)
半监督学习(Semi-Supervised learning)
强化学习(Reinforcement learning)
在课程中,主要学习监督学习和无监督学习,掌握经典的算法。
监督学习
监督学习简单理解就是有目标值,又主要分为回归问题和分类问题。
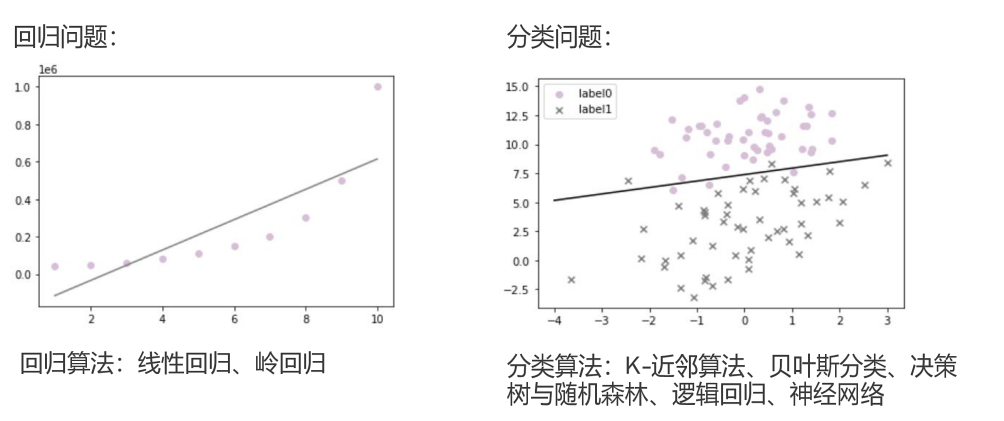
房价、电影的预测数据就是有明确的目标值。下图展示的回归问题,训练出来的模型是 y=kx+b,把x和y作为数据进行传入,训练出k=2,当x为3时,可以预测y为6。回归算法分为线性回归(一元、多元)、岭回归。
还有分类问题,如下图预测红白细胞,如label0为白细胞,label1为红细胞,有明确的目标值,或者是红细胞或者白细胞,通过一条线把红细胞和白细胞分割开,有点号和叉号相互分布在其他区域,这为误差。分类问题的算法:K-近邻算法、贝叶斯分类、决策树与随机森林、逻辑回归、神经网络。
无监督学习
无监督学习意味着输入数据没有被标记,也没有确定的结果(无具体目标)。样本数据类别未知,需要根据样本间的相似性对样本集进行分类(趋向于聚类的过程),试图使类内差距最小化,类间差距最大化。如对不同的图形,本身没有分类,可以根据图形间的间距来进行划分,距离比较近的划分为一类,使用的算法是:K-means、Dbscan、PCA降维手段。
总结:
监督学习,有标签(目标值),可以做分类或者回归
无监督学习,没有标签(无目标值),可以做聚类
半监督学习
半监督学习可以简单理解为一部分数据有目标,而另一部分数据无目标。主要用于监督学习效果不能满足需求时,使用半监督学习来增强学习效果。
增强学习
增强学习主要用于自动进行决策,并可以做连续决策。整个过程都是动态的,上一步数据的输出就是下一步数据的输入。
好比人类进行的动作,用于阿尔法狗,下棋的时候,不停的快速的进行决策。告诉模型,下棋的规则,让自己跟自己去博弈,但只用三天时间就打败了下棋第一人,时间越长就越厉害。
模型评估(非常重要)
模型训练出来并不是直接使用,而是要进行模型评估,对于比较优秀的模型才会真实的投入使用,模型评估是非常重要的。
模型评估是模型开发过程中不可或缺的一部分,有助于发现表达数据的最佳模型和所选模型将来工作的性能如何。
模型评估是用来评估模型误差的大小,在模型中放入测试数据,得到预测结果跟真实结果的差异即为误差,误差越小,模型越优秀。
误差主要分为:
- 经验误差:在训练集上的误差,相当于课后做章节练习
- 泛化误差:对未知数据上的误差,相当于学习后期末考试
思考:只有一个包含m个样例的数据集,x为特征,y为目标,
D
=
{
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
.
.
.
.
.
,
(
x
m
,
y
m
)
}
D= \{ (x_1,y_1),(x_2,y_2),.....,(x_m,y_m) \}
D={(x1,y1),(x2,y2),.....,(xm,ym)},此时这个数据可能既要去训练模型,又要去测试这个模型的好坏,这样可靠吗?
这样是不可靠的,好比在考试前做了一套一模一样的考试题,此时的考试就没有作用了,一组数据既做训练又做测试,就会失去原本的效果。我们需要对数据进行划分,分为训练集和测试集。一部分数据用于测试,一部分用于训练。
经验误差
保留测试集的方法
- 留出法:股票10年的历史数据进行模型训练,前8年做训练集,后2年做测试集。数据分布的不是很均匀,比如股票前8年亏损,后2年盈利,打破了原有连续数据的分布。也可以7,3分等。
留出法的实现方式:
1.直接划分为以N成训练集与M成测试集,
2.每层数据随机抽取N成训练集与随机抽取M成测试集。

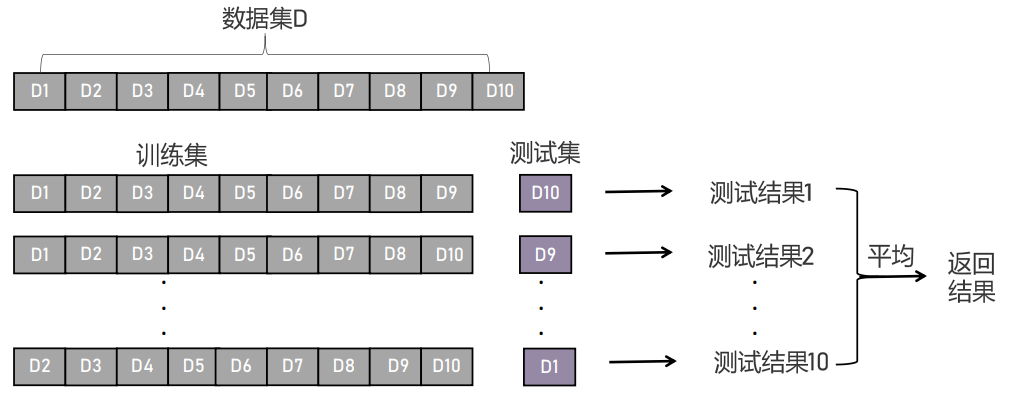
- K折交叉验证:把每一份数据均做一次测试集,把测试结果求平均得到返回结果。适合在数据量小的情况下使用,对计算力要求比较高,如把数据集D分为10等份,前9份作为训练集,最后1份作为测试集得到测试结果1;将1-8份和第10份作为训练集,第9份作为测试集得到测试结果2;依次类推最后把2-10份作为训练集,第1份作为测试集得到测试结果10,把得到的10个结果进行平均返回结果。
K折交叉验证的实现方式:把数据集分为10份,每次从数据集中选取9份为训练集,1份作为测试集,去训练模型得到测试结果,最后把得到的10次的测试结果进行平均得到返回结果。但是此方法适合在数据量比较少的情况下进行。当数据量比较大时,对电脑的计算力要求比较高。
- 自助法(有放回的抽取样本):给定包含m个样本的数据集D,对它采样得到数据集D’,每次随机从D中挑选一个样本,拷贝到D’,再将该样本放回初始数据集D中,使得该样本下次采样时仍有可能被采到,执行m次后,就得到一个包含m个样本的数据集D’,这就是自主采样的结果。
留出法和K折交叉验证法的缺陷:
从原样本中保留了一部分样本数据作为测试集,导致训练集的数据小于原集合,样本数据的规模不同,会有偏差;
自助法是随机的有放回的抽取样本,去构建训练集,保留了数据的随机性,训练集和测试集不影响原本的个数,解决了留出法和K折交叉验证法的缺陷,。
比如有10个数,原样本为:{1,2,3,4,5,6,7,8,9,10},可直接进行训练
随机有放回的抽取 : {2,2,3,5,4,6,7,8,2,1},可以出现重复值
选中的概率为:1/10
没有选中的概率为 1-1/10
10次未选中的概率为 (1-1/10)^10
m次就为(1-1/m)^m
自助法的实现过程中,D中有一部分样本在D’中多次出现,另一部分样本不出现。那么样本m在采样中始终不被采到的概率是 ( 1 − 1 m ) m (1-\frac{1}{m})^m (1−m1)m,取极限得到: lim n → + ∞ ( 1 − 1 m ) m = 1 e \lim_{n\rightarrow+\infty} (1-\frac{1}{m})^m=\frac{1}{e} n→+∞lim(1−m1)m=e1
三种方法用于训练集和测试集的划分。
训练集好比课本知识;验证集好比作业或模拟考试,用于调参,比如在集成算法中调出最优的参数;测试集好比是考试。验证集、训练集均可进行调参,训练集调参的样本数量会比较大,速度会受影响,抽取验证集进行调参会大大减少对速度的影响,它们三者是6,2,2的划分样本集。
性能度量
性能度量是评估模型的指标,在预测任务中,给定数据集
D
=
{
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
.
.
.
.
.
,
(
x
m
,
y
m
)
}
D=\{(x_1,y_1),(x_2,y_2),.....,(x_m,y_m)\}
D={(x1,y1),(x2,y2),.....,(xm,ym)},x为特征,y为目标值,其中
y
i
y_i
yi(第i个样本的y值)是
x
i
x_i
xi的真实值,
f
(
x
i
)
f(x_i)
f(xi)为预测值。如果需要评估该模型的性能,我们需将真实值
y
i
y_i
yi与预测值
f
(
x
i
)
f(x_i)
f(xi)进行比较。误差为预测值与真实值之间的差距。
回归任务中,最常用的性能度量是"均方误差"(Mean Squared Error)
M
S
E
=
∑
i
=
1
m
(
f
(
x
i
)
−
y
i
)
2
m
MSE=\frac{\displaystyle \sum^{m}_{i=1}(f(x_i)-y_i)^2}{m}
MSE=mi=1∑m(f(xi)−yi)2
例如:
数据集为:{(1,2),(2,4),(3,5)}
预测值为:{(1,3),(2,4),(3,6)}
均方误差为:((3-2)^2+(4-4)^2+(6-5)^2)/3
更一般的,对于数据分别D和概率密度函数p(.),均方误差可描述为:
M
S
E
=
∫
x
→
d
(
f
(
x
)
−
y
)
2
p
(
x
)
d
x
MSE={\displaystyle \int_{x \to d}(f(x)-y)^2}p(x)dx
MSE=∫x→d(f(x)−y)2p(x)dx
通常数据并不是只有真实值和预测值,还有概率的问题,假如出现的概率为 0.3,0.5,0.2,均方误差就为:((3-2)^2*0.3+(4-4)^2-0.5+(6-5)^2*0.2)/3
- 错误率:
分类错误的样本数占样本总数的比例,如有5个样本,有2个样本分类错误,错误率为:2/5
E ( f ; D ) = 1 m ∑ i = 1 m I I ( f ( x i ) ≠ y i ) E(f;D)=\frac{1}{m}\displaystyle \sum^{m}_{i=1}\Iota\Iota({f(x_i) \neq y_i}) E(f;D)=m1i=1∑mII(f(xi)=yi)
当预测值不等于真实值的时候,说明分类错误,出现一次计分为1,分类正确计分为0,公式为将计分求和,代表总的出错除以总样本的数据。 - 精准率:
分类正确的样本数占样本总数的比例 a c c ( f ; D ) = 1 m ∑ i = 1 m I I ( f ( x i ) = y i ) = 1 − E ( f ; D ) acc(f;D)=\frac{1}{m}\displaystyle \sum^{m}_{i=1}\Iota\Iota({f(x_i) = y_i})=1-E(f;D) acc(f;D)=m1i=1∑mII(f(xi)=yi)=1−E(f;D)
预测值与真实值完全相同的话,计分为1,将计分求和除以总个数就是精准率,也可以写为1-错误率。
常用的错误率和精准率不能满足所有的需求,比如有以下数据:
数据集 D = [1,2,3,4,5,6,7,8,9,10],做一下二分类,如果数据为5是正确的,结果为1;不为5则是错误的,结果为0,分类有明确的类别,错误率为:9/10。
单看这两个指标,会存在一个问题:模型很一般,结果却很好。这时还需要其他的指标,如查准率和查全率。

真实情况和预测结果都分为正例和反例。
假如有100个样本数据,真实情况: y y y 为1,0,1…,其中正例60个,反例40个;预测数据: y ~ \tilde{y} y~为0,1,0,1…,其中正例70个,反例30个。此时,真实情况中整理为60,反例为40;预测结果中正例为70个,反例为30个;假如真正例为50个,则假正例就为70-50=20个,假反例为60-50=10个,假正例为30-10=20个。
此时查准率为:50/(50+20);查全率为:50/(50+10) - 查准率:
正确预测为正占全部预测为正的比例: P = T P T P + F P P=\frac{TP}{TP+FP} P=TP+FPTP
也即是预测的结果中有多少是真实的。 - 查全率:
正确预测为正占全部正样本的比例: R = T P T P + F N R=\frac{TP}{TP+FN} R=TP+FNTP
也即是真实情况中有多少是预测出来的。
泛化误差
预测数据集的误差,泛化误差的评估标准为拟合情况。拟合情况为模型评估用于评价训练好的模型的表现效果,其表现效果大致可分为两类:欠拟合、过拟合。
欠拟合
比如现在训练来人脸识别的模型,把人脸的图片传进去,提取特征,建立数据特征,机器学习到的人的特征为 眼睛、鼻子、嘴巴,把有类似特征的图片传进去后也识别为了人。由于机器学习的人的特征太少,所以有眼睛、鼻子、嘴巴特征的都被识别成了人,也就将猩猩也识别成了人。

过拟合
所建的机器学习模型或深度模型的训练样本中表现的过于优越,导致在验证数据集以及测试数据集中表现不佳。

由于机器学习的特征很多并且单一,提取的特征过于优越,认为人都是黄皮肤的,若有黑皮肤的留学生进行识别,则会将其归类为未知,这也就是过拟合。
小结
进行模型训练需要准备的工作:
1.要有历史数据
- 对数据的划分
- 连续的数据(如:1-10)+有目标值的数据(有明确的目标,如标签)
- 离散的数据(分类的类别)+有目标值的数据
- 无目标值的数据。
- 数据表中行列的意义,在一组数据中
- 行代表样本,一行代表一组样本
- 列代表特征,比如预测房价,要知道房子的面积、地理位置、楼层等均为该房子所具备的特征。
获取到的历史数据不能直接进行模型训练,如爬虫中得到的数据有些内容没有显示完全,经过数据分析进行处理保存的时候就会有缺失值;记录的数据也会有缺失值,所以要对数据进行基本的处理。
2.数据处理
要求数据坚持的原则是完全合一
- 完,指整个数据要是完整的(行列标签完整);
- 全,指数据没有缺失值的,对缺失值进行处理(数据清洗)
- 合,指数据一定要合法,合乎常理,有效的(如年龄不为负值等)
- 一,指数据要唯一,要对数据进行去重,归一化(量纲不同时),单位不同时进行统一单位。
3.特征工程(偏好归纳)
数据的特征并不是每一个都是我们想要的,并非都对算法模型有作用,我们要进行降维,所以我们要选择对算法模型有用的最优特征。这个步骤重中之重,有专业的人士去做。
4.算法模型
- 有监督:有目标的,每时每刻都在目标的监督下工作
- 无监督:没有目标的
- 半监督:二者混合
- 强化:有非常快速的学习方式,如阿尔法狗的算法,作为了解。
5.模型评估
有了模型之后,并不是立即传入数据进行预测结果,还要进行模型评估,现有的模型能否满足要求。
- 经验评估:如培养学生进行知识点的授课,然后进行练习,考核等,不停的测试才能知道学生的学习的情况。将整体的数据集划分为训练集(课本知识)、测试集(考试测试)和验证集(练习),对三个类型的划分有三种方式。
- 留出法:从整体的数据样本中留出一部分作为测试或者验证集,第一种是直接切断,从10个样本中切出6,2,2,会导致不同时间段中数据呈现的周期不一样;第二种是分层,每次都从数据集中选取60%作为数据。
- k折交叉验证法:1.将数据等分未k份,2.每1份轮着做测试集,3.对结果求均值。
缺点:数据量比较大的话会特别浪费时间 - 自助法:有放回的随机抽样。
- 泛化评估
- 欠拟合,提取的特征少
- 过拟合,提取的特征过于优越






![[疑难杂症2023-002]不就是Move一个文件吗,怎么会有这么多坑呢?](https://img-blog.csdnimg.cn/9b9b6d94ad06489cad0dfb769f0b7922.png)

![[oeasy]python0054_三引号_原样显示字符串_triple_quoted](https://img-blog.csdnimg.cn/img_convert/2d22c3f18467ce499d910464429003a0.png)