（牛客）小杜跑酷

news2024/9/20 16:44:30

链接：https://ac.nowcoder.com/acm/contest/49244/F?&headNav=acm
来源：牛客网

题目描述
小杜又在玩游戏了！这回他玩的是跑酷游戏！
已知该跑酷地图长为n，有3层，可以理解为一张3×n的地图。令人新奇的是，这张跑酷地图有一些弹射机关。假设玩家现在位置为(x,y)(x,y)。
每一秒钟，如果玩家没有踩到机关，玩家可以正常向前移动一格；如果玩家踩到机关，即当前玩家位置上存在一个机关，弹射机关会立即随机触发以下一种状态：

上升：将玩家向上向前弹射一格，即将玩家瞬间移动到( max(1,x-1) , y+1 )(max(1,x−1),y+1)；
跳跃：将玩家向前弹射两格，即将玩家瞬间移动到( x , min(n,y+2) )(x,min(n,y+2))；
下降：将玩家向下向前弹射一格，即将玩家瞬间移动到( min(3,x+1) , y+1 )(min(3,x+1),y+1)。
如下图所示。

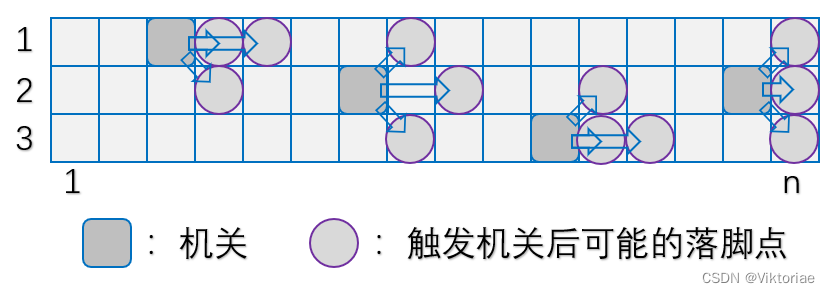
在这里插入图片描述

已知小杜起始位于(1,1)(1,1)，求小杜最终到达(1,n)(1,n), (2,n)(2,n), (3,n)(3,n)的方案数（对998244353取模）。
（如果两种方案被认为是不同的，那么至少存在一个机关，触发的状态不同）

输入描述:
第一行包括n,m\ (2≤ n≤ 10^9,1≤ m≤ 5*10^5)n,m (2≤n≤10
9
,1≤m≤5∗10
5
)，分别表示跑酷地图的长度和其中包含的机关个数；
接下去m行，每行包括两个正整数x,y\ (1≤ x≤ 3,1≤ y≤ n-1)x,y (1≤x≤3,1≤y≤n−1)，代表弹射机关的位置在(x,y)(x,y)（保证任意两个机关位置不同）。

输出描述:
输出三行三个正整数，第ii行代表最终到达(i,n)(i,n)的方案数，答案对 998244353 取模。
示例1
输入
复制
16 4
1 3
2 7
3 11
2 15
输出
复制
5
2
4
示例2
输入
复制
10 1
1 9
输出
复制
2
1
0

思路：

考虑动态规划，先将机关按y值排序，考虑经过(x,y)的方案数，容易推导出：
如果该位置有机关， dp[max(1,x-1)][min(n,y+1)]+=dp[x][y]， dp[min(3,x+1)][min(n,y+1)]+=dp[x][y]， dp[x][min(n,y+2)]+=dp[x][y]；如果该位置没有机关， dp[x][min(n,y+1)]+=dp[x][y] ；
但是，这边的n有10^9，因此我们只需要考虑有机关的dp值。当该单元格不存在机关时，我们可以直接将该单元格的值传递到同层的后一个机关处，将每层机关排序预处理，可以使用二分直接找到后一个机关的位置。时间复杂度O(mlogm)
dp转移时，只需要考虑那些有机关的，以及会被机关转移到的地方，其余地方都为0

#include <iostream>
#include <array>
#include <vector>
#include <algorithm>
using namespace std;
typedef long long ll;
const int mod = 998244353;

int main() {
    ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
    int n, m;
    cin >> n >> m;
    vector<array<int, 2>> traps(m + 1);
    vector<int> nums;
    for (int i = 0; i < m; ++ i) {
        cin >> traps[i][0] >> traps[i][1];
        nums.push_back(min(traps[i][1], n));
        nums.push_back(min(traps[i][1] + 1, n));
        nums.push_back(min(traps[i][1] + 2, n));
    }
    sort(nums.begin(), nums.end());
    nums.erase(unique(nums.begin(), nums.end()), nums.end());
    int siz = (int)nums.size();
    auto id = [&](int v) {
        return lower_bound(nums.begin(), nums.end(), v) - nums.begin() + 1;
    };
    vector<vector<bool>> h(4, vector<bool>(siz + 3, 0));
    vector<vector<ll>> dp(4, vector<ll>(siz + 3, 0));
    for (int i = 0; i < m; ++ i) {
        h[traps[i][0]][id(traps[i][1])] = 1;
    }
    dp[1][1] = 1; // 方案数
    for (int i = 1; i <= siz - 1; ++ i) {
        for (int j = 1; j <= 3; ++ j) {
            if (h[j][i]) {
                dp[max(1, j - 1)][i + 1] = (dp[max(1, j - 1)][i + 1] + dp[j][i]) % mod;
                // 注意是siz不是n
                dp[j][min(siz, i + 2)] = (dp[j][min(siz, i + 2)] + dp[j][i]) % mod;
                dp[min(3, j + 1)][i + 1] = (dp[min(3, j + 1)][i + 1] + dp[j][i]) % mod;
            } else {
                dp[j][i + 1] = (dp[j][i + 1] + dp[j][i]) % mod;
            }
        }
    }
    cout << dp[1][siz] << '\n' << dp[2][siz] << '\n' << dp[3][siz];
}