- 命题逻辑
- 谓词逻辑
- 知识图谱推理
- 因果推理
3.1 命题逻辑
逻辑和推理是基于知识的操作。
命题逻辑是应用一套形式化规则对以符号表示的描述性陈述进行推理的系统。在命题逻辑中,一个或真或假的描述性陈述被称为原子命题,对原子命题的内部结构不做任何解析。若干原子命题可通过逻辑运算符构成复合命题。
任何一个命题或为真、或为假或在给定条件下无法判断(需要进一步的条件约束)。可通过命题联结词对已有命题进行组合,得到新命题。这些通过命题联结词得到的命题被称为复合命题。
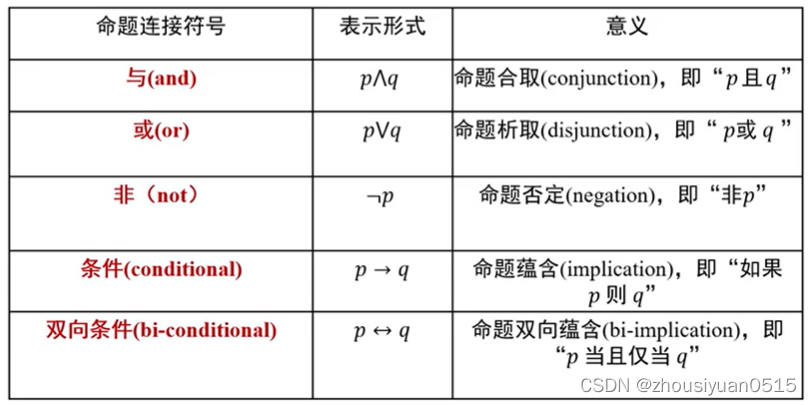
逻辑等价:给定命题p和命题q,如果p和q在所有情况下都具有同样真假结果,那么p和q在逻辑上等价。
逻辑等价为命题进行形式转换带来了可能,基于这些转换不再需要逐一列出p和q的真值表来判断两者是否在逻辑上等价,而是可直接根据已有逻辑等价公式来判断p和q在逻辑上是否等价。

命题逻辑中的推理规则
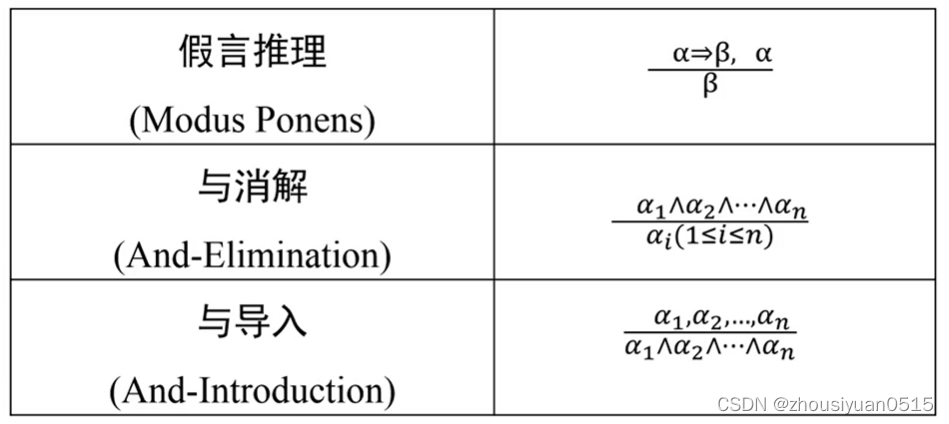

命题范式:
- 有限个简单合取式构成的析取式称为析取范式。
- 由有限个简单析取式构成的合取式称为合取范式。
- 析取范式与合取范式统称为范式。
- 一个析取范式是不成立的,当且仅当它的每个简单合取式都不成立。
- 一个合区范式是成立的,当且仅当它的每个简单析取式都是成立的。
- 任一命题公式都存在着与之等值的析取范式与合区范式。
3.2 谓词逻辑
命题逻辑的局限性:在命题逻辑中,每个陈述句是最基本的单位,无法对原子命题进行分解。因此在命题逻辑中,不能表达局部与整体、一般与个别的关系。不同原子命题蕴含个体、群体和关系等内在丰富语义,命题逻辑无法表现内在丰富语义。因此,需要分析原子命题,分离其主语(个体或群体)和谓语(关系)。
在谓词逻辑中,将原子命题进一步细化,分解出个体、谓词和量词,来表达个体与总体的内在联系和数量关系,这就是谓词逻辑研究内容。
谓词与个体:P(x),P是谓词,x是个体。
量词:
- 全称量词:表示一切的、凡是的、所有的、每一个等,表示定义域内所有个体。
- 存在量词:表示存在、有一个、某些等,表示定义域中存在一个或若干个个体。
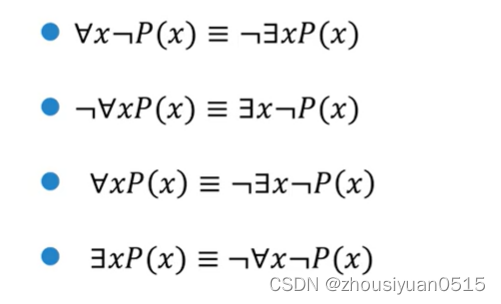
函数与谓词的区别:
- 函数用个体带入结果仍然是个体;
- 谓词用个体带入后就变成了命题;
- 函数是从定义域到值域的映射,谓词是从定义域到命题(真假)的映射。
谓词逻辑的推理规则

自然语言的形式化



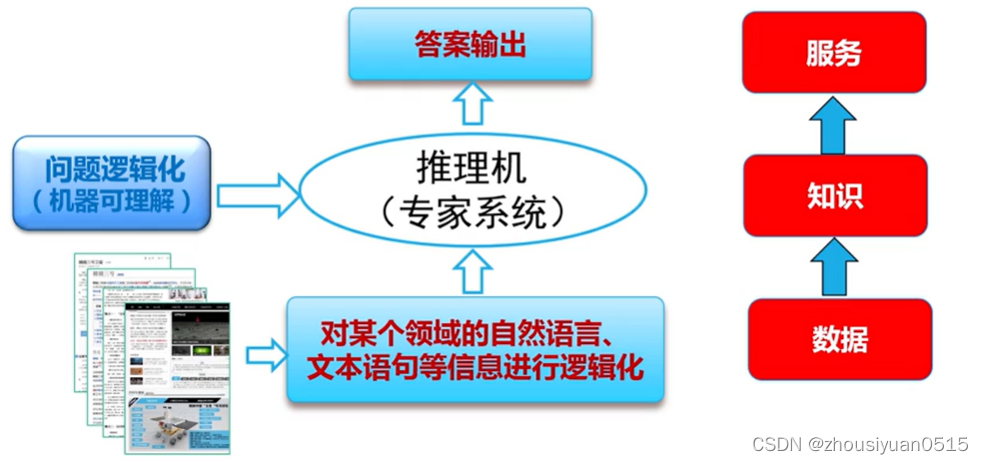
3.3 知识图谱
知识图谱可视为包含多种关系的图。在图中,每个节点是一个实体(如人名、地名、事件和活动等),任意两个节点之间的边表示这两个节点之间存在的关系。
知识图谱构成:
- 概念之间层次化关系
- 概念对应的例子或实体
- 概念或实体的属性:属性是对概念或实体内涵的描述
- 概念与实体之间的关系
- 概念或实体的属性描述和关系表达一般通过三元组来表示
构成:
- 概念:层次化组织
- 实体:概念的示例化描述
- 属性:对概念或实体的描述信息
- 关系:概念或实体之间的关联
- 推理规则:可产生语义网络中上述新的元素
知识图谱通过多关系图表示。
归纳逻辑程序设计是机器学习和逻辑程序设计交叉领域的研究内容。ILP使用一阶谓词逻辑进行只是表示,通过修改和扩充逻辑表达式对现有知识进行归纳,完成推理任务。
FOIL

推理思路:从一般到特殊,逐步给目标添加前提约束谓词,知道所构成的推理规则不覆盖任何反例。