在这里插入图片描述

🚀write in front🚀
📝个人主页：认真写博客的夏目浅石.
🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝
📣系列专栏：AcWing算法学习笔记
💬总结：希望你看完之后，能对你有所帮助，不足请指正！共同学习交流 🖊
✉️如果无聊的话，就来逛逛我的博客栈吧stack-frame.cn

文章目录

前言
一、二分查找的思想
二、二分查找的模板
- 1.寻找⼀个数（基本的⼆分搜索）
- 2.边界问题
- 3.寻找左侧边界的⼆分搜索
- 4.寻找右侧边界的⼆分查找
三、经典题目集
- 总结

前言

在这里插入图片描述
关于我写这篇博客的目的以及原因

其实很早前我就写过博客关于二分法，但是我是不满意的或是我觉得不完美的，于是寒假我又花费三天时间又学了一次，今天就把我所学到的经验和知识输出出来，以供复习和学习。
声明：这里知识基于算法小抄与深入浅出的程序设计两本书+AcWing算法课（侵权删）

提示：以下是本篇文章正文内容，下面案例可供参考

一、二分查找的思想

由于找一个数遍历的时间复杂度有些题目会超时，所以就需要一个更加优秀的算法—二分查找算法，其实二分算法可以将时间复杂度缩小到logN 想一想为什么？

那么废话不多说，下面就来讲二分查找的基本思想：
我们开始定义两个变量，left，right分别指向数组的左端点和右端点（这里会出现左闭右开以及都是闭区间的边界问题，这个问题下面单独会讲解，大家不用着急）

利用数学上边的二分法就是一次检查一半，这样就可以一次去除一半的不符合要求的数据，大大加大了效率，通过不断地迭代，进而二分出正确答案。

二、二分查找的模板

1.寻找⼀个数（基本的⼆分搜索）

这个场景是最简单的，肯能也是⼤家最熟悉的，即搜索⼀个数，如果存在，
返回其索引，否则返回 -1。

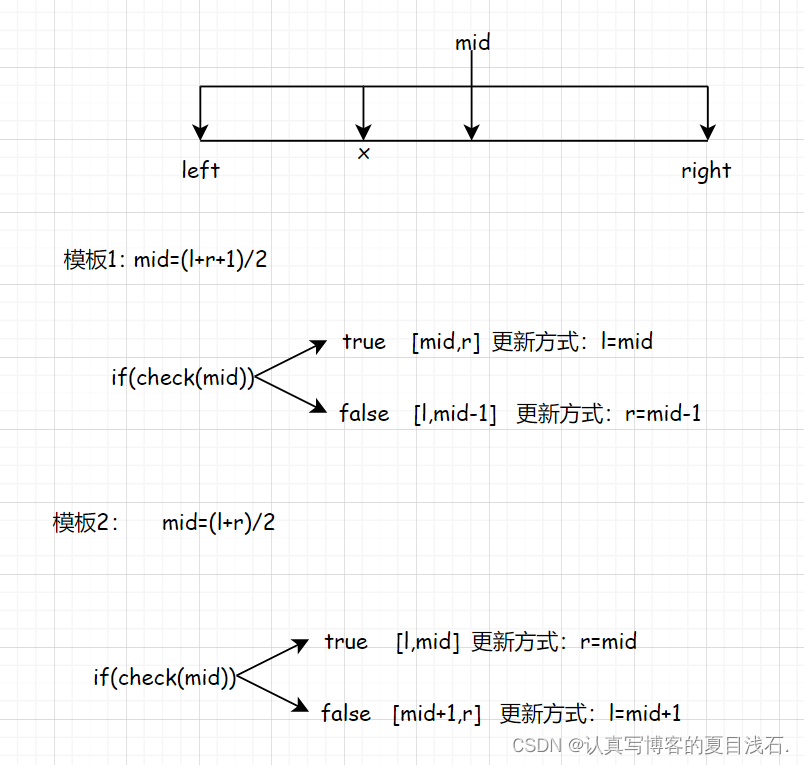
在这里插入图片描述
这里再把二分模板的代码附上：
这里是一个左闭右开区间

					//数组 		//目标    //数组长度 
int binarySearch(int* nums, int target, int size)
{
	//特殊情况，可以了解一下这里不计入模板 
	//if(nums==NULL||size==0)
	//	return -1;
	
	int left=0,right=size-1;
	while(left<right)
	{
		int mid=left+(right-left)/2;//防止溢出
		if(nums[mid]>=target) r=mid;
		else l=mid+1;
	}
	if(nums[left]!=target) return -1;
	else return left; 
}

这里是一个左右都闭的方法

					//数组 		//目标    //数组长度 
int binarySearch(int* nums, int target, int size)
{
	//特殊情况，可以了解一下这里不计入模板 
	//if(nums==NULL||size==0)
	//return -1;
	
	int left=0,right=size-1;
	while(left<=right)
	{
		if(nums[mid] == target)
			return mid;
		else if (nums[mid] < target)
			left = mid + 1; // 注意
		else if (nums[mid] > target)
			right = mid - 1; // 注意
	}
	if(nums[left]!=target) return -1;
	else return left; 
}

2.边界问题

1、为什么 while 循环的条件中是 <=，⽽不是 <？
因为初始化 right 的赋值是 size - 1 ，即最后⼀个元素的索
引，⽽不是 size 。

这⼆者可能出现在不同功能的⼆分查找中，区别是：前者相当于两端都闭区
间 [left, right] ，后者相当于左闭右开区间 [left, right) ，因为索引⼤
⼩为 size 是越界的。

我们这个算法中使⽤的是前者 [left, right] 两端都闭的区间。这个区间
其实就是每次进⾏搜索的区间。

什么时候应该停⽌查找呢？当然，找到了⽬标值的时候可以终⽌：

if(nums[mid] == target)
	return mid;

但如果没找到，就需要 while 循环终⽌，然后返回 -1。那 while 循环什么时
候应该终⽌？查找区间为空的时候应该终⽌，意味着你没得找了，就等于没
找到嘛。

while(left <= right) 的终⽌条件是 left == right + 1 ，写成区间的形式
就是 [right + 1, right] ，或者带个具体的数字进去 [3, 2] ，可⻅这时候
区间为空，因为没有数字既⼤于等于 3 ⼜⼩于等于 2 的吧。所以这时候
⼆分查找解题套路框架
while 循环终⽌是正确的，直接返回 -1 即可。
while(left < right) 的终⽌条件是 left == right ，写成区间的形式就是
[left, right] ，或者带个具体的数字进去 [2, 2] ，这时候区间⾮空，还
有⼀个数 2，但此时 while 循环终⽌了。也就是说这区间 [2, 2] 被漏掉
了，索引 2 没有被搜索，如果这时候直接返回 -1 就是错误的。

当然，如果你⾮要⽤ while(left < right) 也可以，我们已经知道了出错的
原因，就打个补丁好了：

//...
while(left < right) {
// ...
}
return nums[left] == target ? left : -1;

2、为什么 left = mid + 1 ， right = mid - 1 ？我看有的代码是 right =
mid 或者 left = mid ，没有这些加加减减，到底怎么回事，怎么判断？

这也是⼆分查找的⼀个难点，不过只要你能理解前⾯的内容，就能够很
容易判断。

本算法的查找区间是两端都闭的，
即 [left, right] 。那么当我们发现索引 mid 不是要找的 target 时，下
⼀步应该去搜索哪⾥呢？

当然是去搜索 [left, mid-1] 或者 [mid+1, right] 对不对？因为 mid 已
经搜索过，应该从搜索区间中去除。

3、此算法有什么缺陷？
我想你应该已经掌握了该算法的所有细节，以及这样处理的原因。但
是，这个算法存在局限性。
⽐如说给你有序数组 nums = [1,2,2,2,3] ， target 为 2，此算法返回的索
引是 2，没错。但是如果我想得到 target 的左侧边界，即索引 1，或者我
想得到 target 的右侧边界，即索引 3，这样的话此算法是⽆法处理的。
⼆分查找解题套路框架

这样的需求很常⻅，你也许会说，找到⼀个 target，然后向左或向右线性搜
索不⾏吗？可以，但是不好，因为这样难以保证⼆分查找对数级的复杂度
了。
我们后续的算法就来讨论这两种⼆分查找的算法。

3.寻找左侧边界的⼆分搜索

					//数组 		//目标    //数组长度 
int binarySearch(int* nums, int target, int size)
{
	//特殊情况，可以了解一下这里不计入模板 
	//if(nums==NULL||size==0)
	//	return -1;
	
	int left=0,right=size;//注意
	while(left<right)
	{
		int mid=left+(right-left)/2;//防止溢出
		if(nums[mid]>=target) r=mid;
		else l=mid+1;
	}
	if(nums[left]!=target) return -1;
	else return left; 
}

1、为什么 while 中是 < ⽽不是 <= ?
⽤相同的⽅法分析，因为 right = size ⽽不是 size - 1 。因此每次循环的「搜索区间」是 [left, right) 左闭右开。
while(left < right) 终⽌的条件是 left == right ，此时搜索区间 [left, left) 为空，所以可以正确终⽌。

PS：这⾥先要说⼀个搜索左右边界和上⾯这个算法的⼀个区别，也是很多
读者问的：刚才的 right 不是 size - 1 吗，为啥这⾥⾮要写成
size 使得「搜索区间」变成左闭右开呢？

因为对于搜索左右侧边界的⼆分查找，这种写法⽐较普遍，我就拿这种写法
举例了，保证你以后遇到这类代码可以理解。你⾮要⽤两端都闭的写法反⽽
更简单，我会在后⾯写相关的代码，把三种⼆分搜索都⽤⼀种两端都闭的写
法统⼀起来，你耐⼼往后看就⾏了。

2、为什么没有返回 -1 的操作？如果 nums 中不存在 target 这个值，怎
么办？
因为要⼀步⼀步来，先理解⼀下这个「左侧边界」有什么特殊含义：
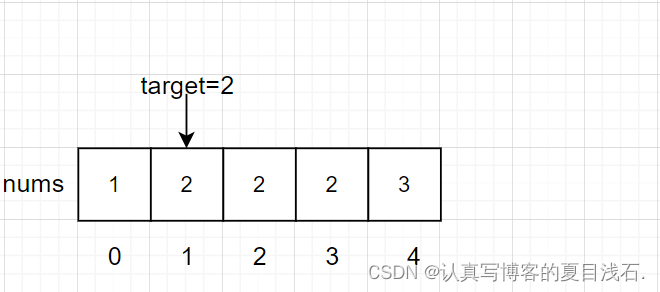
在这里插入图片描述
对于这个数组，算法会返回 1。这个 1 的含义可以这样解读： nums 中⼩于
2 的元素有 1 个。

⽐如对于有序数组 nums = [2,3,5,7] , target = 1 ，算法会返回 0，含义
是： nums 中⼩于 1 的元素有 0 个。
再⽐如说 nums = [2,3,5,7], target = 8 ，算法会返回 4，含义是： nums
中⼩于 8 的元素有 4 个。
⼆分查找解题套路框架

综上可以看出，函数的返回值（即 left 变量的值）取值区间是闭区间
[0, size] ，所以我们简单添加两⾏代码就能在正确的时候 return
-1;

3、为什么 left = mid + 1 ， right = mid ？和之前的算法不⼀样？
这个很好解释，因为我们的「搜索区间」是 [left, right) 左闭右
开，所以当 nums[mid] 被检测之后，下⼀步的搜索区间应该去掉 mid 分
割成两个区间，即 [left, mid) 或 [mid + 1, right) 。

4、为什么返回 left ⽽不是 right ?
都是⼀样的，因为 while 终⽌的条件是 left == right 。

int left_bound(int[] nums, int target)
{
	int left = 0, right = nums.length - 1;
	// 搜索区间为 [left, right]
	while (left <= right)
	{	
		int mid = left + (right - left) / 2;
		if (nums[mid] < target) {
		// 搜索区间变为 [mid+1, right]
		left = mid + 1;
		}
		else if (nums[mid] > target) 
		{
			// 搜索区间变为 [left, mid-1]
			right = mid - 1;
		} 
		else if (nums[mid] == target) 
		{
			// 收缩右侧边界
			right = mid - 1;
		}
	}
}
// 检查出界情况
	if (left >= nums.length || nums[left] != target)
		return -1;
	return left;
}

4.寻找右侧边界的⼆分查找

int right_bound(int[] nums, int target)
{
	int left = 0, right = nums.length - 1;
	// 搜索区间为 [left, right]
	while (left <= right)
	{	
		int mid = left + (right - left) / 2;
		if (nums[mid] < target) {
		// 搜索区间变为 [mid+1, right]
		left = mid + 1;
		}
		else if (nums[mid] > target) 
		{
			// 搜索区间变为 [left, mid-1]
			right = mid - 1;
		} 
		else if (nums[mid] == target) 
		{
			// 收缩右侧边界
			left = mid - 1;
		}
	}
}
// 检查出界情况
	if (lright < 0 || nums[right] != target)
		return -1;
	return right;
}

思路类似左边界。

三、经典题目集

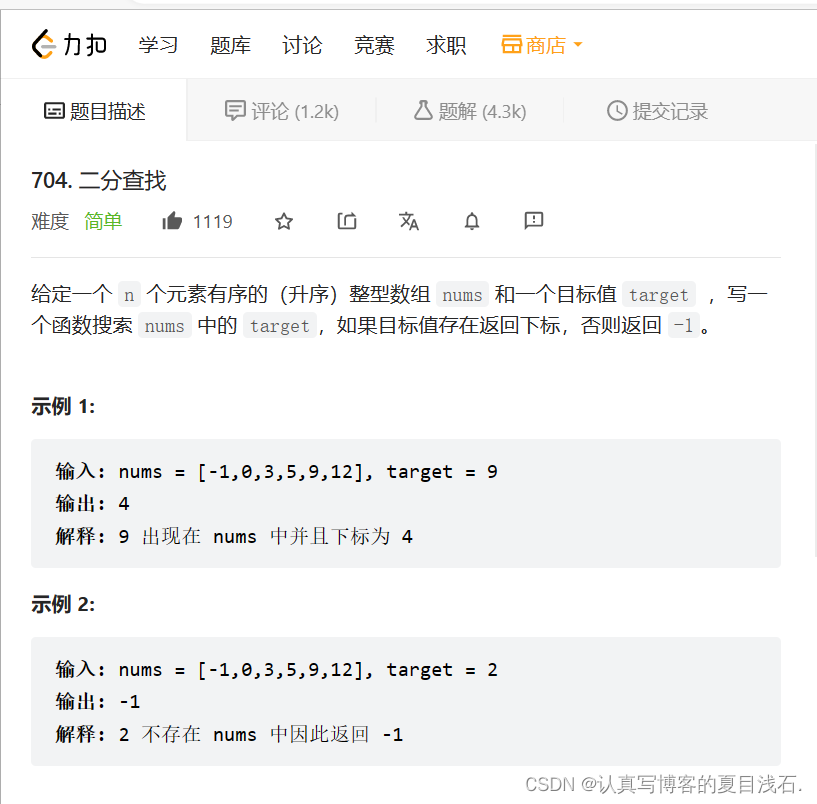
在这里插入图片描述

int search(int* nums, int numsSize, int target)
{
    int left=0,right=numsSize-1;
    while(left<=right)
    {
        int mid=left+(right-left)/2;
        if(nums[mid]==target)
        {
            return mid;
        }
        else if(nums[mid]>target)
        {
            right=mid-1;
        }
        else if(nums[mid]<target)
        {
            left=mid+1;
        }
    }
    return -1;
}
// int search(int* nums, int numsSize, int target)
// {
//     int left=0,right=numsSize-1;
//     while(left<right)
//     {
//         int mid=(right+left)/2;
//         if(nums[mid]>=target) right=mid;
//         else left=mid+1;
//     }
//     if(nums[left]!=target) return -1;
//     else return left;
// }

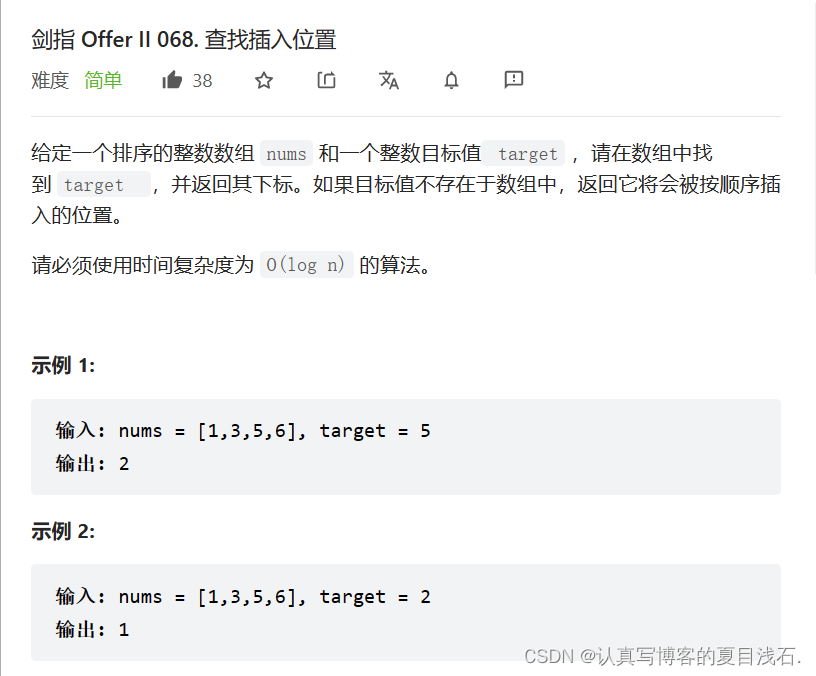
在这里插入图片描述

int searchInsert(int* nums, int numsSize, int target)
{
    int left=0,right=numsSize-1,ans=numsSize;
    while(left<=right)
    {
        int mid=left+(right-left)/2;
        if(nums[mid]>=target)
        {
            ans=mid;
            right=mid-1;
        }
        else left=mid+1;
    }
    return ans;
}


// {
//     int left=0,right=numsSize;
//     while(left<right)
//     {
//         int mid=(left+right)/2;
//         if(nums[mid]>=target) right=mid;
//         else left=mid+1;
//     }
//     return left;
// }

在这里插入图片描述

/*
 * 输入 **matrix 是长度为 matrixSize 的数组指针的数组，其中每个元素（也是一个数组）
 * 的长度组成 *matrixColSize 数组作为另一输入，*matrixColSize 数组的长度也为 matrixSize
 */                     //二维数组         //数组长度         //一维数组       //目标数字
bool findNumberIn2DArray(int** matrix, int matrixSize, int* matrixColSize, int target)
{
    if(matrix==NULL || matrixSize==0 || *matrixColSize==0)
        return false;
    
    int row=matrixSize; //行数
    int col=matrixColSize[0]; 
    
    int i=0;
    int j=col-1;
    while(i<row && j>=0)
    {
        if(matrix[i][j]==target) return true;
        else if(matrix[i][j]>target) j--;
        else if(matrix[i][j]<target) i++;
    }

    return false;
}

总结

1、分析⼆分查找代码时，不要出现 else，全部展开成 else if ⽅便理解。
2、注意「搜索区间」和 while 的终⽌条件，如果存在漏掉的元素，记得在
最后检查。
3、如需定义左闭右开的「搜索区间」搜索左右边界，只要在 nums[mid] == target 时做修改即可，搜索右侧时需要减⼀。
4、如果将「搜索区间」全都统⼀成两端都闭，好记，只要稍改 nums[mid] ==target 条件处的代码和返回的逻辑即可，推荐拿⼩本本记下，作为⼆分搜索模板。

我是夏目浅石，希望和你一起学习进步，刷题无数！！！希望各位大佬能一键三连支持一下博主，hhhh~我们下期见喽

特别注意：本次博客基于算法小抄以及AcWing算法课写出来的内容如果想进一步学习，希望您可以自己看书+看视频。

在这里插入图片描述