简介
本文是为操作系统作业而实现的红黑树源码。作业题目选题为:“(3)红黑树(rbtree)数据结构介绍及其在Linux内核中的应用(结合内核源码进行分析,内核版本号不低于2.6.0)”。
因为网上太多红黑树原理的讲解了,不需要再去讲解原理,所以在这就提供一些讲原理不错的博客,然后主要是给红黑树代码的实现(链接:https://pan.baidu.com/s/15clWdClNPnHA3bd-2FAcqQ 提取码:1234 ),用的c++语言模板实现红黑树,并附带详细注释。(目前只实现了红黑树的插入与查询操作,并可视化打印红黑树)。
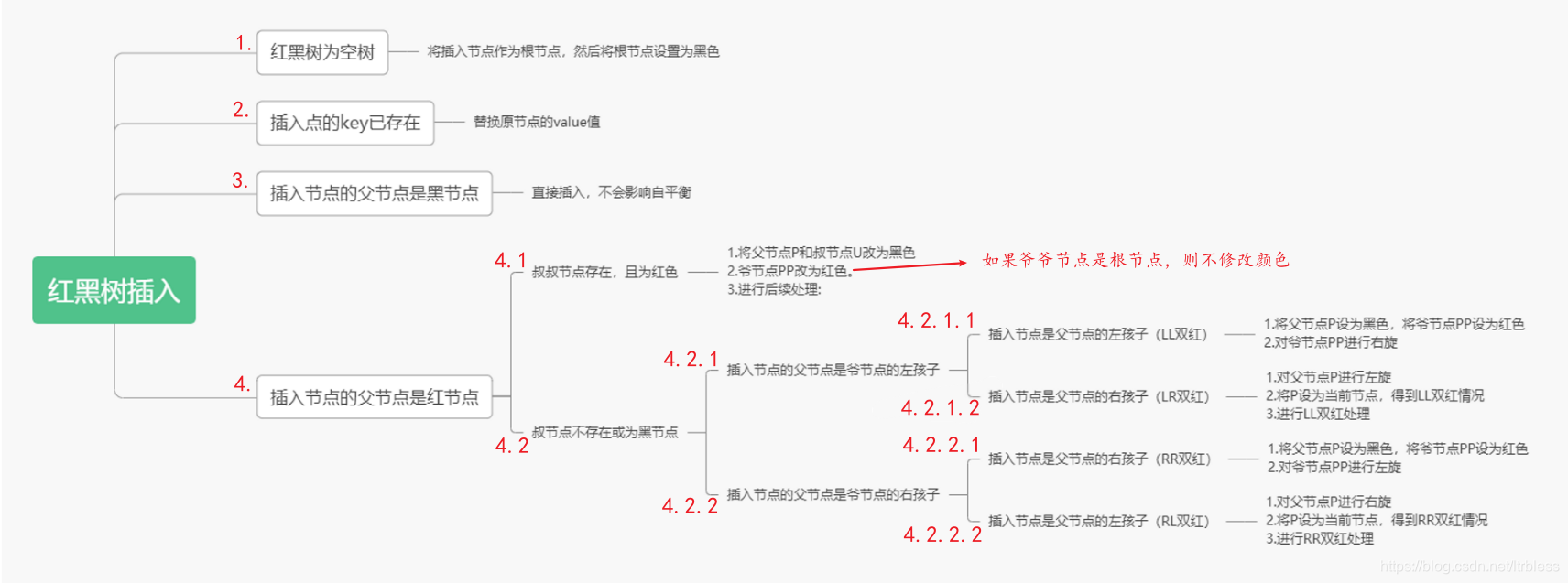
红黑树插入操作的流程图:(参考:红黑树总结 - lukazan - 博客园 (cnblogs.com),该博客用图详细解释了红黑树插入操作的事件,然后我用红色对其事件进行了编号,以便于和代码注释相对应)

编辑
红黑树的本质其实就是2-3树,在上面推荐的博客中也有提到。
代码实现
目录结构:


编辑
build 为构建目录
inlcude 为头文件目录(因为用到了c++模板,将类的定义与实现都写入该hpp文件中,这样比较方便,如果打算分开写到头文件.h与源文件.cpp中也是可以的,不过需要加上 #include"xxx.cpp",具体原因自行百度)
src 为源代码目录,在这里就是测试使用红黑树类的源文件
CMakeLists.txt:
cmake_minimum_required(VERSION 3.0)
project(RedBlackTree)
include_directories(${CMAKE_SOURCE_DIR}/include)
aux_source_directory(${CMAKE_SOURCE_DIR}/include/ Sources)
add_executable(main ${CMAKE_SOURCE_DIR}/src/main.cpp ${Sources})
include--RBTreeNode.hpp:
#ifndef _RBTREENODE_HPP_#define _RBTREENODE_HPP_enumColor// 1 is red,0 is black node
{
Black = 0,
Red
};
template<typename T>
classRBTreeNode
{
public :
T data;
Color color; // 1 代表红色, 0 代表黑色
RBTreeNode* father; // 父节点
RBTreeNode* left; // 左孩子
RBTreeNode* right; // 右孩子public :
RBTreeNode();
voidRBTreeNodeSet(T data); // 配合默认构造函数使用,使用默认构造函数没有初始值,但每个节点必须包含值,所以该函数可以另外设置初始值或者修改初始值RBTreeNode(T data);
~RBTreeNode();
};
template<typename T>
RBTreeNode<T>::RBTreeNode() : color(Red), father(nullptr), left(nullptr), right(nullptr)
{
}
template<typename T>
RBTreeNode<T>::RBTreeNode(T data) : data(data), color(Red) , father(nullptr), left(nullptr), right(nullptr)
{
}
template<typename T>
void RBTreeNode<T>::RBTreeNodeSet(T data)
{
this->data = data;
}
template<typename T>
RBTreeNode<T>::~RBTreeNode()
{
this->father = nullptr;
this->left = nullptr;
this->right = nullptr;
}
#endif
include--RBTree.hpp:
#ifndef _RBTREE_HPP_#define _RBTREE_HPP_#include"RBTreeNode.hpp"#include<iostream>usingnamespace std;
template<typename T>
voidFreeTree(RBTreeNode<T>* curNode);
template<typename T>
classRBTree
{
public :
RBTreeNode<T>* treeRoot;
public :
RBTree();
RBTree(RBTreeNode<T>* node);
~RBTree();
friendvoidFreeTree(RBTreeNode<T>* curNode); // 释放红黑树的内存boolInsert(T data); // 插入节点boolRightRotate(RBTreeNode<T>* curNode); // 右旋boolLeftRotate(RBTreeNode<T>* curNode); // 左旋boolGet(T data); // 查看数据是否存在voidViewTree(RBTreeNode<T>* curNode); // 查看树的结构voidOutput(RBTreeNode<T>* curNode, bool left, string const& indent); // 可视化红黑树voidViewTreeByGraphic(RBTreeNode<T>* curNode); // 可视化红黑树
};
template<typename T>
RBTree<T>::RBTree() : treeRoot(nullptr)
{
}
template<typename T>
RBTree<T>::RBTree(RBTreeNode<T>* node) : treeRoot(node) {}
template<typename T>
RBTree<T>::~RBTree()
{
FreeTree(treeRoot);
}
template<typename T>
voidFreeTree(RBTreeNode<T>* curNode){
if(curNode->right) FreeTree(curNode->right);
if(curNode->left) FreeTree(curNode->left);
if(curNode != nullptr) // 回溯删除所有节点,释放堆上的内存
{
// cout << "This node is deleted : " << curNode->data << '\n';delete curNode;
curNode = nullptr;
return ;
}
}
template<typename T>
bool RBTree<T>::Insert(T data)
{
if(treeRoot == nullptr) // 1. 红黑树为空树的情况,将节点作为根节点,并且设置为黑色
{
treeRoot = newRBTreeNode<T>(data);
treeRoot->color = Black;
return1;
}
RBTreeNode<T>* tmpTreeRoot = treeRoot;
RBTreeNode<T>* curNode = newRBTreeNode<T>(data); // 当前需要插入的节点int flag = -1; // 标记是插入左边还是右边或者是值相等,左边用1标记,右边用2标记,相等用3标记。while(tmpTreeRoot != nullptr) // 查找需要插入节点的父节点
{
if(curNode->data < tmpTreeRoot->data) // 在当前节点的左边
{
if(tmpTreeRoot->left != nullptr) tmpTreeRoot = tmpTreeRoot->left; // 往左走else{
flag = 1; // 左边break; // 如果左边是空的,那么该空的位置就应该插入新的节点,所以跳出
}
}
elseif(curNode->data > tmpTreeRoot->data)
{
if(tmpTreeRoot->right != nullptr) tmpTreeRoot = tmpTreeRoot->right; // 往右走else{
flag = 2; // 右边break;
}
}
else
{
tmpTreeRoot->data = curNode->data;
flag = 3; // 相等break;
}
}
// 查看插入时父节点的相关数据// cout << "Insert data = " << data << " flag = " << flag << " father data = " << tmpTreeRoot->data << " color = " << tmpTreeRoot->color << '\n';// 目前 tmpTreeRoot 为需要插入的节点的父节点if(flag == 3) return1; // 2. 插入点为Key已存在的情况if(flag == 1) // 插入节点
{
tmpTreeRoot->left = curNode;
curNode->father = tmpTreeRoot;
}
elseif(flag == 2)
{
tmpTreeRoot->right = curNode;
curNode->father = tmpTreeRoot;
}
if(tmpTreeRoot->color == Black) return1; // 3. 如果父节点为黑色,返回// cout << "hello\n";// 4. 插入节点的父节点为红色,需要修复
RBTreeNode<T>* uncleNode = nullptr;
while( curNode->father != nullptr && // 当前节点不是根节点
curNode->father->father != nullptr && // 当前节点有爷爷节点
curNode->father->color == Red) // 当前节点的父节点是红色节点
{
// grandfather// / \ // / \ // father ?(4.1)// / \ //(4.2.1)? ?(4.2.2)
RBTreeNode<T>* fatherNode = curNode->father;
RBTreeNode<T>* grandFatherNode = fatherNode->father;
if(fatherNode == grandFatherNode->left) // 4.2.1 父节点为左子树
{
uncleNode = grandFatherNode->right;
if(uncleNode != nullptr && uncleNode->color == Red) // 4.1 叔叔节点存在且为红色
{
fatherNode->color = Black;
uncleNode->color = Black;
if(grandFatherNode->father != nullptr) grandFatherNode->color = Red; // 如果为空那么该节点是父节点,不能是红色
curNode = grandFatherNode;
}
else// 4.2 叔叔节点为空节点或者为黑色节点
{
if(curNode == fatherNode->left) // 4.2.1.1 当前节点在父节点的左边,LL(双红的情况)// 1. 将父节点设置为黑色,将爷爷节点设置为红色// 2. 对爷爷节点进行右旋
{
fatherNode->color = Black;
grandFatherNode->color = Red;
RightRotate(grandFatherNode); // 右旋
}
elseif(curNode == fatherNode->right) // 4.2.1.2 当前节点的父节点的右边,LR双红
{
curNode = curNode->father;
LeftRotate(curNode);
}
}
}
// grandfather// / \ // / \ // ?(4.1) father// / \ // (4.2.1)? ?(4.2.2)else// 4.2.2 父节点为右子树
{
uncleNode = grandFatherNode->left;
if(uncleNode != nullptr && uncleNode->color == Red)
// 4.1 叔叔节点存在,且为红色。// 叔叔节点的判断位置有些乱,是因为理论要先能找到叔叔节点,// 所以需要先进行4.2.1/2节的判断,也就是插入节点的父节点是爷爷节点的左孩子还是右孩子
{
fatherNode->color = Black;
uncleNode->color = Black;
if(grandFatherNode->father != nullptr) grandFatherNode->color = Red;
curNode = grandFatherNode;
}
else
{
if(curNode == fatherNode->right) // 4.2.2.1 RR 双红
{
fatherNode->color = Black;
grandFatherNode->color = Red;
LeftRotate(grandFatherNode);
}
elseif(curNode == fatherNode->left)// 4.2.2.2 RL双红
{
curNode = curNode->father;
RightRotate(curNode);
}
}
}
}
return1;
}
template<typename T>
bool RBTree<T>::RightRotate(RBTreeNode<T>* curNode)
{
RBTreeNode<T>* curNodeLeft = curNode->left;
RBTreeNode<T>* curNodeFather = curNode->father;
// 操作1 :把当前节点的左孩子换成当前节点的左节点的右孩子
curNode->left = curNodeLeft->right;
if(curNode->left != nullptr) curNode->left->father = curNode; // 判断当前节点的左节点的右孩子是否为空// 操作2 :把当前节点的作为当前节点的左节点的右孩子
curNodeLeft->right = curNode;
curNode->father = curNodeLeft;
// 操作3 :把当前节点的父节点与当前节点的左节点进行连接if(curNodeFather == nullptr) // curNodeLeft为根节点
{
curNodeLeft->father = curNodeFather;
treeRoot = curNodeLeft; // 这里需要注意,需要把根节点更新
}
elseif(curNodeFather->left == curNode)
{
curNodeFather->left = curNodeLeft;
curNodeLeft->father = curNodeFather;
}
else
{
curNodeFather->right = curNodeLeft;
curNodeLeft->father = curNodeFather;
}
return1;
}
template<typename T>
bool RBTree<T>::LeftRotate(RBTreeNode<T>* curNode)
{
RBTreeNode<T>* curNodeRight = curNode->right;
RBTreeNode<T>* curNodeFather = curNode->father;
// 操作1 :把当前节点的右孩子换成当前节点的右节点的左孩子
curNode->right = curNodeRight->left;
if(curNode->right != nullptr) curNode->right->father = curNode;
// 操作2 :把当前节点的作为当前节点的右节点的左孩子
curNodeRight->left = curNode;
curNode->father = curNodeRight;
// 操作3 :把当前节点的父节点与当前节点的右节点进行连接if(curNodeFather == nullptr) // curNodeRight 为根节点
{
curNodeRight->father = curNodeFather;
treeRoot = curNodeRight; // 更新根节点// cout << "root data = " << treeRoot->data << '\n';
}
elseif(curNodeFather->right == curNode) // 当前节点为当前节点父节点的右孩子
{
curNodeFather->right = curNodeRight;
curNodeRight->father = curNodeFather;
}
else// 当前节点为当前节点父节点的左孩子
{
curNodeFather->left = curNodeRight;
curNodeRight->father = curNodeFather;
}
}
template<typename T>
bool RBTree<T>::Get(T data)
{
RBTreeNode<T>* tmpRoot = treeRoot;
while(tmpRoot != nullptr)
{
if(data < tmpRoot->data) // 往左
{
if(tmpRoot->left != nullptr) tmpRoot = tmpRoot->left;
elsebreak;
}
elseif(data > tmpRoot->data) // 往右
{
if(tmpRoot->right != nullptr) tmpRoot = tmpRoot->right;
elsebreak;
}
else// 找到了
{
return1;
}
}
return0; // 未找到
}
template<typename T>
void RBTree<T>::ViewTree(RBTreeNode<T>* curNode) // 线序遍历打印红色树查看正确性
{
cout << curNode->data << ' ';
if(curNode->left != nullptr) ViewTree(curNode->left);
if(curNode->right != nullptr) ViewTree(curNode->right);
}
template<typename T>
void RBTree<T>::Output(RBTreeNode<T>* curNode, bool left, string const& indent)
{
if (curNode->right)
{
Output(curNode->right, false, indent + (left ? "| " : " "));
}
cout << indent;
cout << (left ? '\\' : '/');
cout << "-----";
cout << curNode->data << "(" << (curNode->color == Red ? 'R' : 'B') << ")" << '\n';
if(curNode->left)
{
Output(curNode->left, true, indent + (left ? " " : "| "));
}
}
template<typename T>
void RBTree<T>::ViewTreeByGraphic(RBTreeNode<T>* curNode)
{
cout << "\n\n-------------------- Red Black Tree ------------------------";
cout << "\n--------------- B : Black Node R : Red Node -------------------\n\n\n";
if(curNode->right)
{
Output(curNode->right, false, "");
}
cout << curNode->data << "(" << (curNode->color == Red ? 'R' : 'B') << ")" << '\n';
if(curNode->left)
{
Output(curNode->left, true, "");
}
cout << "\n\n------------------------------------------------------------\n";
}
#endif
src--main.cpp
#include<iostream>#include<cstring>#include<sstream>#include"RBTree.hpp"#include"RBTreeNode.hpp"usingnamespace std;
int a[30] = {0, 12, 1, 9, 2, 0, 11, 7, 19, 4, 15, 18, 5, 14, 13, 10, 16, 6, 3, 8, 17};
intmain(){
RBTree<int> Tree;
cout << "\nOrder of inserting of all nodes.\n\n";
for(int i = 1; i <= 20; i++ )
{
cout << a[i] << ' ';
Tree.Insert(a[i]); // 插入节点
}
cout << '\n';
cout << "\nPre-order traversal of red-black tree : \n\n";
Tree.ViewTree(Tree.treeRoot); // 红黑树的线序遍历
Tree.ViewTreeByGraphic(Tree.treeRoot); // 可视化红黑树// for(int i = 1; i <= 20; i++ )// {// cout << i << " : " << Tree.Get(a[i]) << '\n';// }
}
Result:
PS C:\CodeWork\Project\DataStructure\RBTree\build> .\main.exe
Order of inserting of all nodes.
12 1 9 2 0 11 7 19 4 15 18 5 14 13 10 16 6 3 8 17
Pre-order traversal of red-black tree :
9 4 1 0 2 3 6 5 7 8 14 12 11 10 13 18 16 15 17 19
-------------------- Red Black Tree ------------------------
--------------- B : Black Node R : Red Node -------------------
/-----19(B)
/-----18(R)
| | /-----17(R)
| \-----16(B)
| \-----15(R)
/-----14(B)
| | /-----13(B)
| \-----12(R)
| \-----11(B)
| \-----10(R)
9(B)
| /-----8(R)
| /-----7(B)
| /-----6(R)
| | \-----5(B)
\-----4(B)
| /-----3(R)
| /-----2(B)
\-----1(R)
\-----0(B)
------------------------------------------------------------
对于这组测试数据的每一步的插入的图的步骤在博客:(7条消息) 红黑树从头至尾插入和删除结点的全程演示图_结构之法 算法之道-CSDN博客_红黑树的插入和删除