全连接神经网络
问题描述
利用numpy和pytorch搭建全连接神经网络。使用numpy实现此练习需要自己手动求导,而pytorch具有自动求导机制。
我们首先先手动算一下反向传播的过程,使用的模型和初始化权重、偏差和训练用的输入和输出值如下:
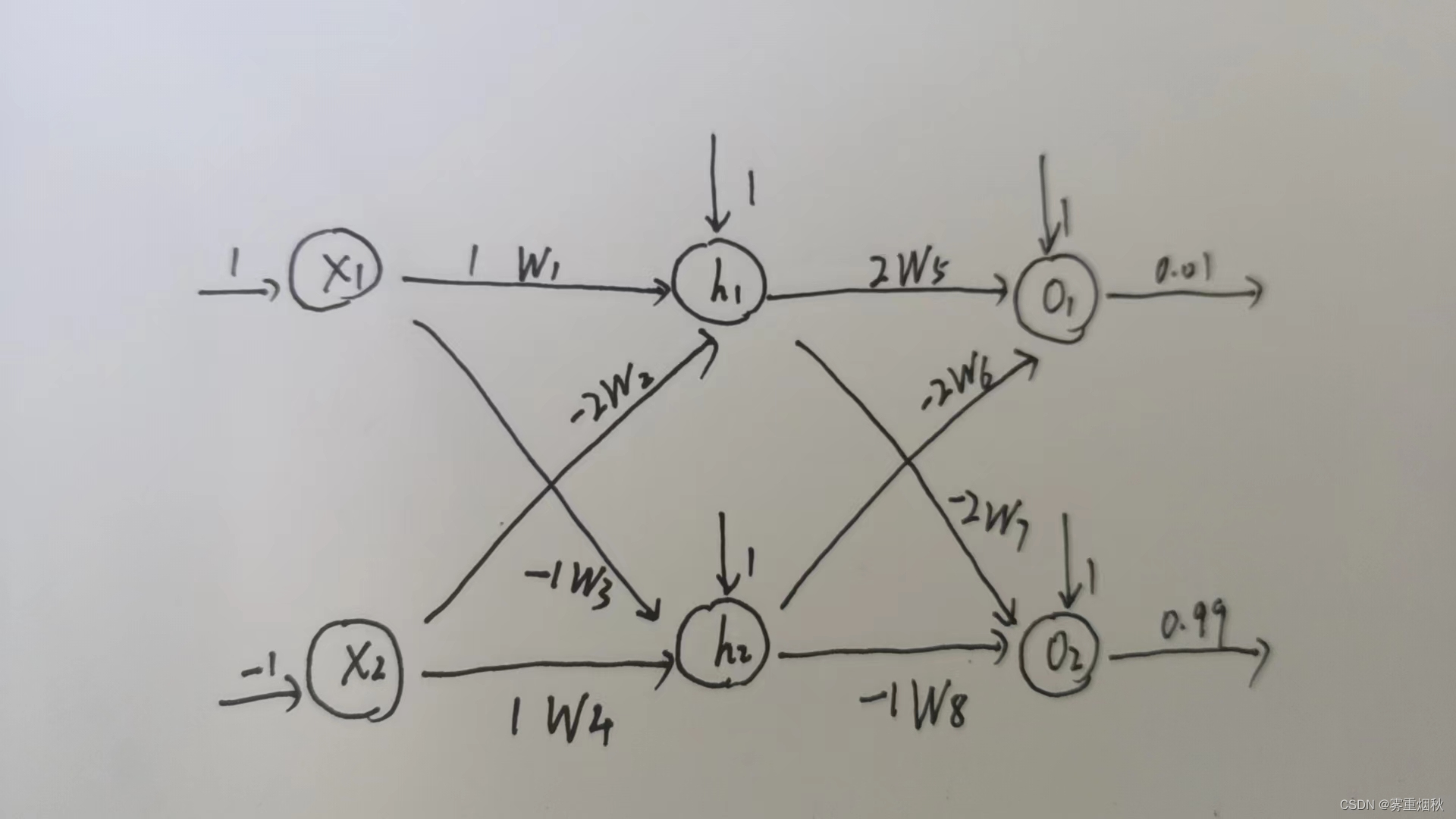
我们看一下正向过程:计算出每个隐藏神经元的输入,通过激活函数(用Sigmoid函数)转换为下一层的输入,直到达到输出层计算最终输出:
先来计算隐藏层h_1的输入,
z
h
1
=
ω
1
x
1
+
ω
2
x
2
+
1
=
1
∗
1
+
(
−
2
)
∗
(
−
1
)
+
1
=
4
z_{h_1}=\omega_1 x_1+\omega_2 x_2 + 1=1*1+(-2)*(-1)+1=4
zh1=ω1x1+ω2x2+1=1∗1+(−2)∗(−1)+1=4
然后用激活函数激活,得到
h
1
h_1
h1的输出
a
h
1
=
σ
(
z
h
1
)
=
1
1
+
e
−
z
h
1
=
1
1
+
e
−
4
=
0.98201379
a_{h_1}=\sigma(z_{h_1})=\frac{1}{1+e^{-z_{h_1}}}=\frac{1}{1+e^{-4}}=0.98201379
ah1=σ(zh1)=1+e−zh11=1+e−41=0.98201379
同理有
z
h
2
=
ω
3
x
1
+
ω
4
x
2
+
1
=
−
1
∗
1
+
1
∗
(
−
1
)
+
1
=
−
1
z_{h_2}=\omega_3 x_1+\omega_4 x_2 + 1=-1*1+1*(-1)+1=-1
zh2=ω3x1+ω4x2+1=−1∗1+1∗(−1)+1=−1
可得
a
h
2
=
σ
(
z
h
2
)
=
0.26894142
a_{h_2}=\sigma(z_{h_2})=0.26894142
ah2=σ(zh2)=0.26894142
这两个输出作为下一层的输入,接下来计算输出层
o
1
o_1
o1:
z
o
1
=
ω
5
∗
a
h
1
+
ω
6
∗
a
h
2
+
1
=
2
∗
0.98201379
+
(
−
2
)
∗
0.26894142
+
1
=
2.42614474
z_{o_1}=\omega_5*a_{h_1}+\omega_6*a_{h_2}+1=2*0.98201379+(-2)*0.26894142+1=2.42614474
zo1=ω5∗ah1+ω6∗ah2+1=2∗0.98201379+(−2)∗0.26894142+1=2.42614474
a
o
1
=
σ
(
z
o
1
)
=
1
1
+
e
−
z
o
1
=
1
1
+
e
−
2.42614474
=
0.91879937
a_{o_1}=\sigma(z_{o_1})=\frac{1}{1+e^{-z_{o_1}}}=\frac{1}{1+e^{-2.42614474}}=0.91879937
ao1=σ(zo1)=1+e−zo11=1+e−2.426144741=0.91879937
同理,得到输出层
o
2
o_2
o2的输出
z
o
2
=
ω
7
∗
a
h
1
+
ω
8
∗
a
h
2
+
1
=
−
2
∗
0.98201379
+
(
−
1
)
∗
0.26894142
+
1
=
−
1.23296900
z_{o_2}=\omega_7*a_{h_1}+\omega_8*a_{h_2}+1=-2*0.98201379+(-1)*0.26894142+1=-1.23296900
zo2=ω7∗ah1+ω8∗ah2+1=−2∗0.98201379+(−1)∗0.26894142+1=−1.23296900
a
o
2
=
σ
(
z
o
2
)
=
1
1
+
e
−
z
o
2
=
1
1
+
e
−
1.23296900
=
0.22566220
a_{o_2}=\sigma(z_{o_2})=\frac{1}{1+e^{-z_{o_2}}}=\frac{1}{1+e^{-1.23296900}}=0.22566220
ao2=σ(zo2)=1+e−zo21=1+e−1.232969001=0.22566220
可以看到,初始参数上的输出和目标值0.01、0.99有不小的距离,下面计算一下总误差
使用均方误差来计算总误差:
E
total
=
1
2
∑
(
y
^
−
y
)
2
E_{\text {total }}=\frac{1}{2} \sum(\hat{y}-y)^2
Etotal =21∑(y^−y)2
其中
y
y
y是输出层的实际输出,
y
^
\hat y
y^是期望输出,比如对于
o
1
o_1
o1神经元,有误差:
E
o
1
=
1
2
(
y
o
1
^
−
y
o
1
)
2
=
1
2
(
0.01
−
0.91879937
)
2
=
0.41295815
E_{o_1}=\frac{1}{2}\left(\hat{y_{o_1}}-y_{o_1}\right)^2=\frac{1}{2}(0.01-0.91879937)^2=0.41295815
Eo1=21(yo1^−yo1)2=21(0.01−0.91879937)2=0.41295815
同理,计算出
E
o
2
=
0.29210614
E_{o_2}=0.29210614
Eo2=0.29210614
总误差即为
E
total
=
E
o
1
+
E
o
2
=
0.41295815
+
0.29210614
=
0.70506429
E_{\text {total }}=E_{o_1}+E_{o_2}=0.41295815+0.29210614=0.70506429
Etotal =Eo1+Eo2=0.41295815+0.29210614=0.70506429
然后进行反向过程,反向传播算法的目的是更高效的计算梯度,从而更新参数值,使得总误差更小,也就是使实际输出更贴近我们期望输出。它是作为一个整体去更新整个神经网络的,反向就是先考虑输出层,然后再考虑上一层,直到输入层。
首先计算输出层:
考虑参数
ω
5
\omega_5
ω5,计算
ω
5
\omega_5
ω5的改变会对总误差有多大的影响,即计算
∂
E
t
o
t
a
l
∂
ω
5
\frac{\partial E_{total}}{\partial \omega_5}
∂ω5∂Etotal,由链式法则有
∂
E
t
o
t
a
l
∂
ω
5
=
∂
E
t
o
t
a
l
∂
a
o
1
∂
a
o
1
∂
z
o
1
∂
z
o
1
∂
ω
5
\frac{\partial E_{total}}{\partial \omega_5}=\frac{\partial E_{total}}{\partial a_{o_1}}\frac{\partial a_{o_1}}{\partial z_{o_1}}\frac{\partial z_{o_1}}{\partial \omega_5}
∂ω5∂Etotal=∂ao1∂Etotal∂zo1∂ao1∂ω5∂zo1
要计算这个等式中的每个式子,首先计算
a
o
1
a_{o_1}
ao1如何影响总误差
E
total
=
1
2
∑
(
target
o
1
−
a
o
1
)
2
+
1
2
(
target
o
2
−
a
o
2
)
2
∂
E
total
∂
a
o
1
=
2
∗
1
2
(
target
o
1
−
a
o
1
)
∗
(
−
1
)
+
0
=
−
(
target
o
1
−
a
o
1
)
=
−
(
0.01
−
0.91879937
)
=
0.90879937
\begin{aligned} & E_{\text {total }}=\frac{1}{2} \sum\left(\text { target }_{o_1-a_{o_1}}\right)^2+\frac{1}{2}\left(\text { target }_{o_2}-a_{o_2}\right)^2 \\ & \frac{\partial E_{\text {total }}}{\partial a_{o_1}}=2 * \frac{1}{2}\left(\text { target }_{o_1-a_{o_1}}\right) *(-1)+0=-\left(\text { target }_{o_1}-a_{o_1}\right)=-(0.01-0.91879937)=0.90879937 \end{aligned}
Etotal =21∑( target o1−ao1)2+21( target o2−ao2)2∂ao1∂Etotal =2∗21( target o1−ao1)∗(−1)+0=−( target o1−ao1)=−(0.01−0.91879937)=0.90879937
接下来计算
∂
a
o
1
∂
z
o
1
\frac{\partial a_{o_1}}{\partial z_{o_1}}
∂zo1∂ao1
我们知道
σ
′
(
z
)
=
σ
(
z
)
(
1
−
σ
(
z
)
)
\sigma'(z)=\sigma(z)(1-\sigma(z))
σ′(z)=σ(z)(1−σ(z))(对sigmoid函数求导证明)
所以
所以
∂
a
o
1
∂
z
o
1
=
a
o
1
(
1
−
a
o
1
)
=
0.91879937
(
1
−
0.91879937
)
=
0.07460709
\text { 所以 } \frac{\partial a_{o_1}}{\partial z_{o_1}}=a_{o_1}\left(1-a_{o_1}\right)=0.91879937(1-0.91879937)=0.07460709
所以 ∂zo1∂ao1=ao1(1−ao1)=0.91879937(1−0.91879937)=0.07460709
最后是
∂
z
o
1
∂
ω
5
\frac{\partial z_{o_1}}{\partial \omega_5}
∂ω5∂zo1
z
o
1
=
ω
5
∗
a
h
1
+
ω
6
∗
a
h
2
+
b
z_o1=\omega_5 * a_{h_1}+\omega_6 * a_{h_2}+b
zo1=ω5∗ah1+ω6∗ah2+b
∂
z
o
1
∂
ω
5
=
a
h
1
=
0.98201379
\frac{\partial z_{o_1}}{\partial \omega_5}=a_{h_1}=0.98201379
∂ω5∂zo1=ah1=0.98201379
最后放到一起得到:
∂
E
t
o
t
a
l
∂
ω
5
=
∂
E
t
o
t
a
l
∂
a
o
1
∂
a
o
1
∂
z
o
1
∂
z
o
1
∂
ω
5
=
0.90879937
∗
0.07460709
∗
0.98201379
=
0.06658336
\frac{\partial E_{total}}{\partial \omega_5}=\frac{\partial E_{total}}{\partial a_{o_1}}\frac{\partial a_{o_1}}{\partial z_{o_1}}\frac{\partial z_{o_1}}{\partial \omega_5}=0.90879937*0.07460709*0.98201379=0.06658336
∂ω5∂Etotal=∂ao1∂Etotal∂zo1∂ao1∂ω5∂zo1=0.90879937∗0.07460709∗0.98201379=0.06658336
通常一般定义
δ
o
1
=
∂
E
t
o
t
a
l
∂
a
o
1
∂
a
o
1
∂
z
o
1
=
∂
E
t
o
t
a
l
∂
z
o
1
\delta_{o_1}=\frac{\partial E_{total}}{\partial a_{o_1}}\frac{\partial a_{o_1}}{\partial z_{o_1}}=\frac{\partial E_{total}}{\partial z_{o_1}}
δo1=∂ao1∂Etotal∂zo1∂ao1=∂zo1∂Etotal
因此,
∂
E
t
o
t
a
l
∂
ω
5
=
δ
o
1
a
h
1
\frac{\partial E_{total}}{\partial \omega_5}=\delta_{o_1}a_{h_1}
∂ω5∂Etotal=δo1ah1
为了减小误差,通常需要更新当前权重,如下:
ω
5
=
ω
5
−
α
∗
∂
E
t
o
t
a
l
∂
ω
5
=
2
−
0.5
∗
0.06658336
=
1.96670832
\omega_5 = \omega_5 - \alpha * \frac{\partial E_{total}}{\partial \omega_5}=2-0.5*0.06658336=1.96670832
ω5=ω5−α∗∂ω5∂Etotal=2−0.5∗0.06658336=1.96670832
同理可以算出其他权重
ω
6
=
−
2.00911750
\omega_6=-2.00911750
ω6=−2.00911750,
ω
7
=
−
1.93442139
\omega_7=-1.93442139
ω7=−1.93442139,
ω
8
=
−
0.98204017
\omega_8=-0.98204017
ω8=−0.98204017
这是输出层的所有参数,接下来需要往前推,更新隐藏层的参数。
首先来更新
ω
1
\omega_1
ω1:
∂
E
t
o
t
a
l
∂
ω
1
=
∂
E
t
o
t
a
l
∂
a
h
1
∂
a
h
1
∂
z
h
1
∂
z
h
1
∂
ω
1
\frac{\partial E_{total}}{\partial \omega_1}=\frac{\partial E_{total}}{\partial a_{h_1}}\frac{\partial a_{h_1}}{\partial z_{h_1}}\frac{\partial z_{h_1}}{\partial \omega_1}
∂ω1∂Etotal=∂ah1∂Etotal∂zh1∂ah1∂ω1∂zh1
要用和更新输出层参数类似的步骤来更新隐藏层的参数,但是不同的是,每个隐藏层的神经元都影响了多个输出层(或下一层)神经元的输出,
a
h
1
a_{h_1}
ah1同时影响了
a
o
1
a_{o_1}
ao1和
a
o
2
a_{o_2}
ao2,因此计算
∂
E
t
o
t
a
l
∂
a
h
1
\frac{\partial E_{total}}{\partial a_{h_1}}
∂ah1∂Etotal需要将输出层的两个神经元都考虑在内:
∂
E
t
o
t
a
l
∂
a
h
1
=
∂
E
o
1
∂
a
h
1
+
∂
E
o
2
∂
a
h
1
\frac{\partial E_{total}}{\partial a_{h_1}}=\frac{\partial E_{o_1}}{\partial a_{h_1}}+\frac{\partial E_{o_2}}{\partial a_{h_1}}
∂ah1∂Etotal=∂ah1∂Eo1+∂ah1∂Eo2,从
∂
E
o
1
∂
a
h
1
\frac{\partial E_{o_1}}{\partial a_{h_1}}
∂ah1∂Eo1开始,有:
∂
E
o
1
∂
a
h
1
=
∂
E
o
1
∂
z
o
1
∗
∂
z
o
1
∂
a
h
1
\frac{\partial E_{o_1}}{\partial a_{h_1}}=\frac{\partial E_{o_1}}{\partial z_{o_1}}* \frac{\partial z_{o_1}}{\partial a_{h_1}}
∂ah1∂Eo1=∂zo1∂Eo1∗∂ah1∂zo1
上面已经算过
∂
E
o
1
∂
z
o
1
=
0.06780288
\frac{\partial E_{o_1}}{\partial z_{o_1}}=0.06780288
∂zo1∂Eo1=0.06780288了(实际上就是
∂
E
t
o
t
a
l
∂
z
o
1
\frac{\partial E_{total}}{\partial z_{o_1}}
∂zo1∂Etotal,因为
E
t
o
t
a
l
E_{total}
Etotal只有
E
o
1
E_{o_1}
Eo1这一项对
z
o
1
z_{o_1}
zo1求导不为0),而且
∂
z
o
1
∂
a
h
1
=
ω
5
=
2
\frac{\partial z_{o_1}}{\partial a_{h_1}}=\omega_5=2
∂ah1∂zo1=ω5=2,所以有
∂
E
o
1
∂
a
h
1
=
0.06780288
∗
2
=
0.13560576
\frac{\partial E_{o_1}}{\partial a_{h_1}}=0.06780288*2=0.13560576
∂ah1∂Eo1=0.06780288∗2=0.13560576
同理,可得
∂
E
o
2
∂
a
h
1
=
−
0.13355945
∗
(
−
2
)
=
0.26711890
\frac{\partial E_{o_2}}{\partial a_{h_1}}=-0.13355945*(-2)=0.26711890
∂ah1∂Eo2=−0.13355945∗(−2)=0.26711890
因此:
∂
E
t
o
t
a
l
∂
a
h
1
=
∂
E
o
1
∂
a
h
1
+
∂
E
o
2
∂
a
h
1
=
0.13560576
+
0.26711890
=
0.40272466
\frac{\partial E_{total}}{\partial a_{h_1}}=\frac{\partial E_{o_1}}{\partial a_{h_1}}+\frac{\partial E_{o_2}}{\partial a_{h_1}}=0.13560576+0.26711890=0.40272466
∂ah1∂Etotal=∂ah1∂Eo1+∂ah1∂Eo2=0.13560576+0.26711890=0.40272466
现在已经知道了
∂
E
t
o
t
a
l
∂
a
h
1
\frac{\partial E_{total}}{\partial a_{h_1}}
∂ah1∂Etotal,还需要计算
∂
a
h
1
∂
z
h
1
\frac{\partial a_{h_1}}{\partial z_{h_1}}
∂zh1∂ah1和
∂
z
h
1
∂
ω
1
\frac{\partial z_{h_1}}{\partial \omega_1}
∂ω1∂zh1:
a
h
1
=
σ
(
z
h
1
)
=
1
1
+
e
−
z
h
1
=
1
1
+
e
−
4
=
0.98201379
a_{h_1}=\sigma(z_{h_1})=\frac{1}{1+e^{-z_{h_1}}}=\frac{1}{1+e^{-4}}=0.98201379
ah1=σ(zh1)=1+e−zh11=1+e−41=0.98201379
∂
a
h
1
∂
z
h
1
=
a
h
1
(
1
−
a
h
1
)
=
0.98201379
(
1
−
0.98201379
)
=
0.01766271
\frac{\partial a_{h_1}}{\partial z_{h_1}}=a_{h_1}(1-a_{h_1})=0.98201379(1-0.98201379)=0.01766271
∂zh1∂ah1=ah1(1−ah1)=0.98201379(1−0.98201379)=0.01766271
z
h
1
=
ω
1
x
1
+
ω
2
x
2
+
b
z_{h_1}=\omega_1 x_1+\omega_2 x_2 + b
zh1=ω1x1+ω2x2+b
∂
z
h
1
∂
ω
1
=
x
1
=
1
\frac{\partial z_{h_1}}{\partial \omega_1}=x_1=1
∂ω1∂zh1=x1=1
最后,总式子就可以计算了:
∂
E
t
o
t
a
l
∂
ω
1
=
∂
E
t
o
t
a
l
∂
a
h
1
∂
a
h
1
∂
z
h
1
∂
z
h
1
∂
ω
1
=
0.40272466
∗
0.01766271
∗
1
=
0.00711321
\frac{\partial E_{total}}{\partial \omega_1}=\frac{\partial E_{total}}{\partial a_{h_1}}\frac{\partial a_{h_1}}{\partial z_{h_1}}\frac{\partial z_{h_1}}{\partial \omega_1}=0.40272466*0.01766271*1=0.00711321
∂ω1∂Etotal=∂ah1∂Etotal∂zh1∂ah1∂ω1∂zh1=0.40272466∗0.01766271∗1=0.00711321
接下来就可以更新
ω
1
\omega_1
ω1
ω
1
=
ω
1
−
α
∗
E
t
o
t
a
l
∂
ω
1
=
0.99644340
\omega_1=\omega_1 - \alpha * \frac{E_{total}}{\partial \omega_1}=0.99644340
ω1=ω1−α∗∂ω1Etotal=0.99644340
同理可以得到:
ω
2
=
−
1.99644340
\omega_2=-1.99644340
ω2=−1.99644340,
ω
3
=
−
0.99979884
\omega_3=-0.99979884
ω3=−0.99979884,
ω
4
=
0.99979884
\omega_4=0.99979884
ω4=0.99979884
在执行10000此更新权重的过程后,误差变成了0.000,输出是0.011851540581436764和0.9878060737917571,这和期望输出0.01和0.99十分接近了。
使用numpy来练习上述过程:
import numpy as np
class Network():
def __init__(self, **kwargs):
self.w1, self.w2, self.w3, self.w4 = kwargs['w1'], kwargs['w2'], kwargs['w3'], kwargs['w4']
self.w5, self.w6, self.w7, self.w8 = kwargs['w5'], kwargs['w6'], kwargs['w7'], kwargs['w8']
self.d_w1, self.d_w2, self.d_w3, self.d_w4 = 0.0, 0.0, 0.0, 0.0
self.d_w5, self.d_w6, self.d_w7, self.d_w8 = 0.0, 0.0, 0.0, 0.0
self.x1 = kwargs['x1']
self.x2 = kwargs['x2']
self.y1 = kwargs['y1']
self.y2 = kwargs['y2']
self.learning_rate = kwargs['learning_rate']
def sigmoid(self, z):
a = 1 / (1 + np.exp(-z))
return a
def forward_propagate(self):
loss = 0.0
b = 1
in_h1 = self.w1 * self.x1 + self.w2 * self.x2 + b
out_h1 = self.sigmoid(in_h1)
in_h2 = self.w3 * self.x1 + self.w4 * self.x2 + b
out_h2 = self.sigmoid(in_h2)
in_o1 = self.w5 * out_h1 + self.w6 * out_h2
out_o1 = self.sigmoid(in_o1)
in_o2 = self.w7 * out_h1 + self.w8 * out_h2
out_o2 = self.sigmoid(in_o2)
loss += (self.y1 - out_o1) ** 2 + (self.y2 - out_o2) ** 2
loss = loss / 2
return out_o1, out_o2, out_h1, out_h2, loss
def back_propagate(self, out_o1, out_o2, out_h1, out_h2):
d_o1 = (out_o1 - self.y1)
d_o2 = (out_o2 - self.y2)
d_w5 = d_o1 * out_o1 * (1 - out_o1) * out_h1
d_w6 = d_o1 * out_o1 * (1 - out_o1) * out_h2
d_w7 = d_o2 * out_o2 * (1 - out_o2) * out_h1
d_w8 = d_o2 * out_o2 * (1 - out_o2) * out_h2
d_w1 = (d_w5 + d_w6) * out_h1 * (1 - out_h1) * self.x1
d_w2 = (d_w5 + d_w6) * out_h1 * (1 - out_h1) * self.x2
d_w3 = (d_w7 + d_w8) * out_h2 * (1 - out_h2) * self.x1
d_w4 = (d_w7 + d_w8) * out_h2 * (1 - out_h2) * self.x2
self.d_w1, self.d_w2, self.d_w3, self.d_w4 = d_w1, d_w2, d_w3, d_w4
self.d_w5, self.d_w6, self.d_w7, self.d_w8 = d_w5, d_w6, d_w7, d_w8
return
def update_w(self):
self.w1 = self.w1 - self.learning_rate * self.d_w1
self.w2 = self.w2 - self.learning_rate * self.d_w2
self.w3 = self.w3 - self.learning_rate * self.d_w3
self.w4 = self.w4 - self.learning_rate * self.d_w4
self.w5 = self.w5 - self.learning_rate * self.d_w5
self.w6 = self.w6 - self.learning_rate * self.d_w6
self.w7 = self.w7 - self.learning_rate * self.d_w7
self.w8 = self.w8 - self.learning_rate * self.d_w8
if __name__ == "__main__":
w_key = ['w1', 'w2', 'w3', 'w4', 'w5', 'w6', 'w7', 'w8']
w_value = [1, -2, -1, 1, 2, -2, -2, -1]
parameter = dict(zip(w_key, w_value))
parameter['x1'] = 1
parameter['x2'] = -1
parameter['y1'] = 0.01
parameter['y2'] = 0.99
parameter['learning_rate'] = 0.5
network = Network(**parameter)
for i in range(10000):
out_o1, out_o2, out_h1, out_h2, loss = network.forward_propagate()
if (i % 1000 == 0):
print("第{}轮的loss={}".format(i,loss))
network.back_propagate(out_o1, out_o2, out_h1, out_h2)
network.update_w()
print("更新后的权重")
print(network.w1, network.w2, network.w3, network.w4, network.w5, network.w6, network.w7, network.w8)
输出为:
第0轮的loss=0.7159242750464174
第1000轮的loss=0.0003399411282644947
第2000轮的loss=0.00012184533000665064
第3000轮的loss=6.271954032855594e-05
第4000轮的loss=3.751394416870217e-05
第5000轮的loss=2.438595788224937e-05
第6000轮的loss=1.6716935251649648e-05
第7000轮的loss=1.1889923562720554e-05
第8000轮的loss=8.688471135735563e-06
第9000轮的loss=6.481437220727472e-06
更新后的权重
0.9057590485430621 -1.9057590485430547 0.4873077189729459 -0.4873077189729459 -1.130913420789734 -3.752510764474653 2.7328131233332877 1.948002277914531
使用pytorch来练习上述过程
import torch
from torch import nn
class Network(nn.Module):
def __init__(self, w_value):
super().__init__()
self.sigmoid = nn.Sigmoid()
self.linear1 = nn.Linear(2, 2, bias=True)
self.linear1.weight.data = torch.tensor(w_value[:4], dtype=torch.float32).view(2, 2)
self.linear1.bias.data = torch.ones(2)
self.linear2 = nn.Linear(2, 2, bias=True)
self.linear2.weight.data = torch.tensor(w_value[4:], dtype=torch.float32).view(2, 2)
self.linear2.bias.data = torch.ones(2)
def forward(self, x):
x = self.linear1(x)
x = self.sigmoid(x)
x = self.linear2(x)
x = self.sigmoid(x)
return x
w_value = [1, -2, -1, 1, 2, -2, -2, -1]
network = Network(w_value)
loss_compute = nn.MSELoss()
learning_rate = 0.5
optimizer = torch.optim.SGD(network.parameters(), lr=learning_rate)
x1, x2 = 1, -1
y1, y2 = 0.01, 0.99
inputs = torch.tensor([x1, x2], dtype=torch.float32)
targets = torch.tensor([y1, y2], dtype=torch.float32)
for i in range(10000):
optimizer.zero_grad()
outputs = network(inputs)
loss = loss_compute(outputs, targets)
if (i % 1000 == 0):
print("第{}轮的loss={}".format(i, loss))
loss.backward()
optimizer.step()
# 最终的权重和偏差
print("权重:")
print(network.linear1.weight)
print(network.linear2.weight)
print("偏差:")
print(network.linear1.bias)
print(network.linear2.bias)
第0轮的loss=0.7050642967224121
第1000轮的loss=0.0001787583896657452
第2000轮的loss=5.7717210438568145e-05
第3000轮的loss=2.7112449970445596e-05
第4000轮的loss=1.487863755755825e-05
第5000轮的loss=8.897048246581107e-06
第6000轮的loss=5.617492206511088e-06
第7000轮的loss=3.6816677493334282e-06
第8000轮的loss=2.4793637294351356e-06
第9000轮的loss=1.704187070572516e-06
权重:
Parameter containing:
tensor([[ 0.9223, -1.9223],
[-0.0543, 0.0543]], requires_grad=True)
Parameter containing:
tensor([[-0.3244, -3.2635],
[ 0.5369, 0.4165]], requires_grad=True)
偏差:
Parameter containing:
tensor([0.9223, 1.9457], requires_grad=True)
Parameter containing:
tensor([-1.3752, 3.5922], requires_grad=True)
函数拟合
问题描述
理论和实验证明,一个两层的ReLU网络可以模拟任何函数[1~5]。请自行定义一个函数, 并使用基于ReLU的神经网络来拟合此函数。
要求
- 请自行在函数上采样生成训练集和测试集,使用训练集来训练神经网络,使用测试集来验证拟合效果。
- 可以使用深度学习框架来编写模型。
from torch.utils.data import DataLoader
from torch.utils.data import TensorDataset
import torch.nn as nn
import numpy as np
import torch
# 准备数据
x1 = np.linspace(-2 * np.pi, 2 * np.pi, 400)
x2 = np.linspace(np.pi, -np.pi, 400)
y = np.sin(x1) + np.cos(3 * x2)
# 将数据做成数据集的模样
X = np.vstack((x1, x2)).T
Y = y.reshape(400, -1)
# 使用批训练方式
dataset = TensorDataset(torch.tensor(X, dtype=torch.float), torch.tensor(Y, dtype=torch.float))
dataloader = DataLoader(dataset, batch_size=100, shuffle=True)
# 神经网络主要结构,这里就是一个简单的线性结构
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.net = nn.Sequential(
nn.Linear(in_features=2, out_features=10), nn.ReLU(),
nn.Linear(10, 100), nn.ReLU(),
nn.Linear(100, 10), nn.ReLU(),
nn.Linear(10, 1)
)
def forward(self, input: torch.FloatTensor):
return self.net(input)
net = Net()
# 定义优化器和损失函数
optim = torch.optim.Adam(Net.parameters(net), lr=0.001)
Loss = nn.MSELoss()
# 下面开始训练:
# 一共训练 1000次
for epoch in range(1000):
loss = None
for batch_x, batch_y in dataloader:
y_predict = net(batch_x)
loss = Loss(y_predict, batch_y)
optim.zero_grad()
loss.backward()
optim.step()
# 每100次 的时候打印一次日志
if (epoch + 1) % 100 == 0:
print("step: {0} , loss: {1}".format(epoch + 1, loss.item()))
# 使用训练好的模型进行预测
predict = net(torch.tensor(X, dtype=torch.float))
# 绘图展示预测的和真实数据之间的差异
import matplotlib.pyplot as plt
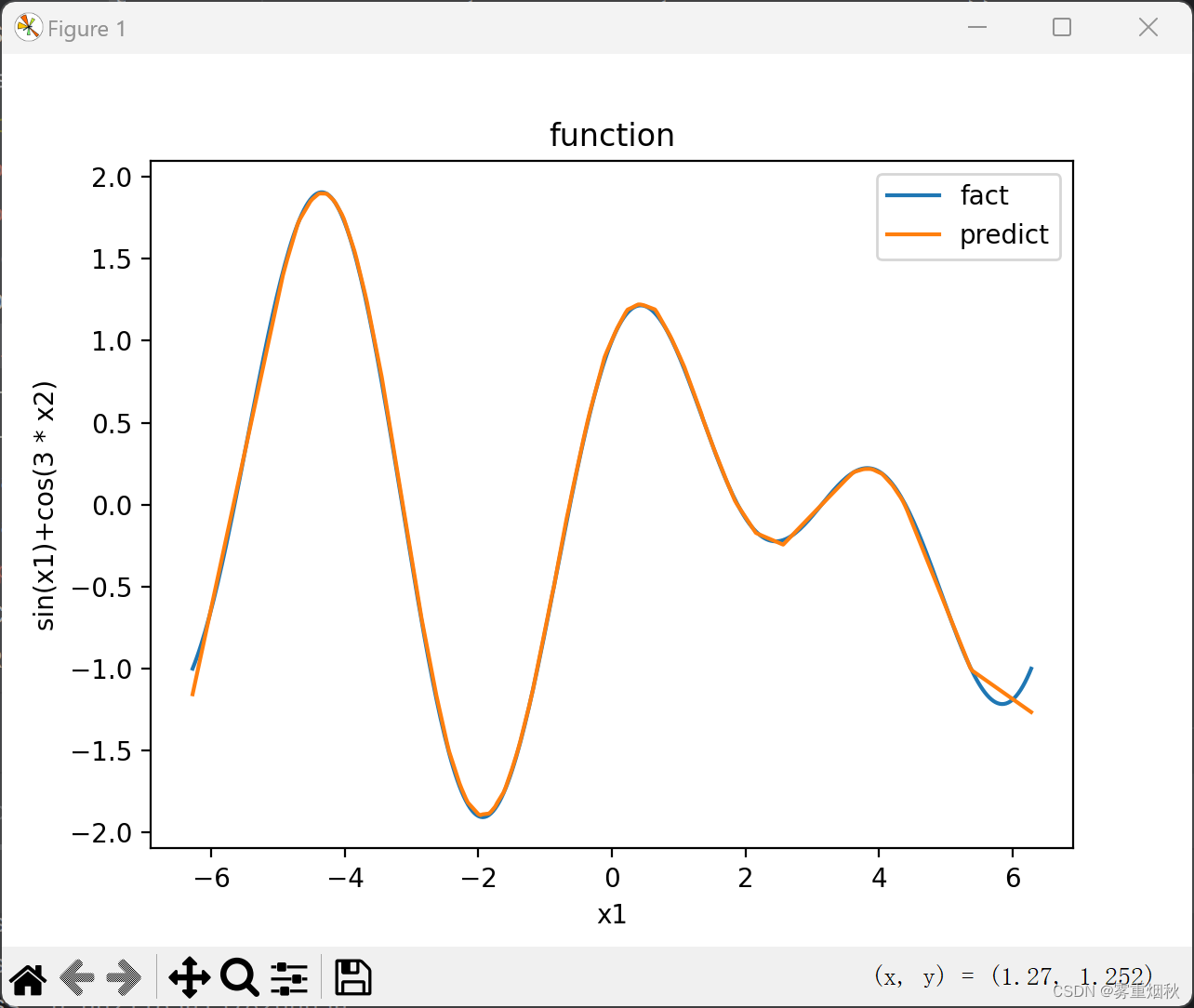
plt.plot(x1, y, label="fact")
plt.plot(x1, predict.detach().numpy(), label="predict")
plt.title("function")
plt.xlabel("x1")
plt.ylabel("sin(x1)+cos(3 * x2)")
plt.legend()
plt.show()
输出:
step: 100 , loss: 0.23763391375541687
step: 200 , loss: 0.06673044711351395
step: 300 , loss: 0.044088222086429596
step: 400 , loss: 0.013059427961707115
step: 500 , loss: 0.010913526639342308
step: 600 , loss: 0.003434327431023121
step: 700 , loss: 0.00702542532235384
step: 800 , loss: 0.001976138213649392
step: 900 , loss: 0.0032644111197441816
step: 1000 , loss: 0.003176396246999502



![【PostgreSQL17新特性之-冗余IS [NOT] NULL限定符的处理优化】](https://img-blog.csdnimg.cn/img_convert/d8c52000ffd33b61ebaa1a0113f46d9c.png)



![[代码复现]Self-Attentive Sequential Recommendation(ing)](https://img-blog.csdnimg.cn/direct/196fac48d6b848fba9abf60f8c7b44bd.png)