一、说明

​​​​​​​数学领域有太多有趣的领域，领域我特别感兴趣。这是一个奇妙的无限、自我复制的分形世界。更有趣的是分形事物总能在大自然中发现对应物，这对渲染自然界和电脑作图有更大发挥。分形维度不是整数维，本文对此稍加介绍。

二、分形到底是什么？

分形是一个在任何尺度上看起来或多或少相同的对象。这意味着无论您如何放大分形，细节看起来几乎相同。

您能给我们举个例子吗？我知道这个问题即将到来，所以我画了一些！这个叫做谢尔宾斯基三角形…

这个叫做龙曲线…

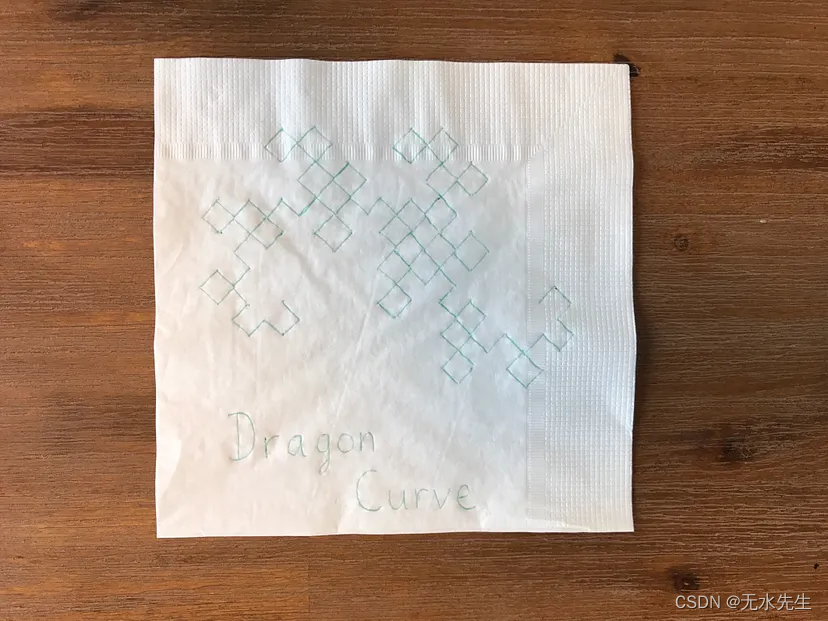
而这个曲线叫做科赫曲线…

我要指出的是，这些都是近似值。实际上，在serviettes上绘制分形是相当棘手的，信不信由你，我无法绘制到无穷小的尺度！所有这些分形都是所谓的自相似分形，这意味着它们的细节在放大时完全相同。这意味着您可以在其内部找到分形的精确副本。

三、更多更深刻的

我喜欢分形的一件事是它们非常直观。一些分形模式（如上面的例子）非常适合涂鸦，因为它们可以通过遵循迭代过程来构造。

一般来说，自相似分形可以从一些“基块”构造，方法是将基块的副本排列在特定的模式中，然后缩小该模式以用作新的“基块”并重复。（该过程也可以在不收缩的情况下完成，这更容易绘制，但占用的空间越来越大）。

以下是以这种方式绘制的上述曲线的几个迭代：

当然，任何这样的构造在你用完空间之前只能进行这么多次迭代，所以物理表示只是真实分形的近似值。然而，如果我们把数学概念一直带到无穷小，事情就会开始变得有点奇怪。

四、引进无穷小会产生什么样的怪事？

每当无穷大涉足数学领域时，你都可以期待有一些东西与你的直觉不完全匹配。如果我告诉你分形不符合我们通常的维度概念呢？

对于传统形状，我们可以通过使用一定的测量单位测量物体来考虑尺寸，然后使用较小的测量单位重新测量，看看您还得到了多少件。

例如，在这里，我画了一条线、一个正方形和一个边长为 1 个“单位”的立方体，然后使用大小为 1/3 的单位重新测量它们。对于直线，现在有 3 = 3¹ 个，对于正方形，有 9 = 3² 个，对于立方体，有 27 = 3³ 个。

​
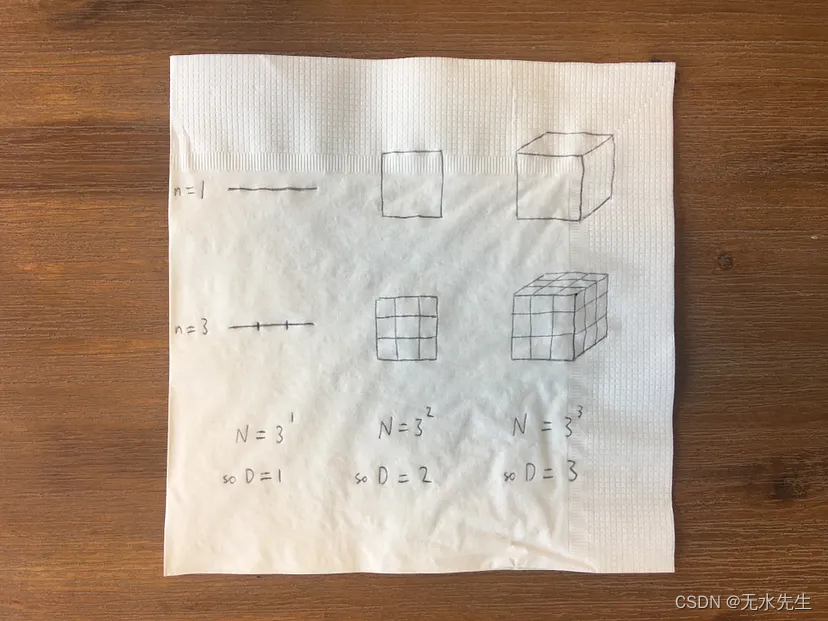
一般来说，如果我们使用大小的 1/n 倍的度量单位并得到 N 个，那么物体的维度 D 满足 N = n^D.（所以直线有 n¹ 个块，正方形有 n² 个块，立方体有 n³ 个块）。重新排列，我们得到 D = ln（N）/ln（n）。目前为止，一切都好。

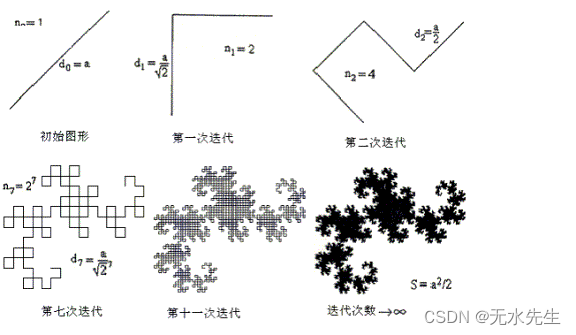
现在让我们来看看科赫曲线。你认为科赫曲线是一维的，这是可以原谅的——毕竟，我们之前使用的迭代结构的每一步都只是将直线放在一起。但这就是无穷大介入并动摇我们的直觉的地方：当我们将这个过程迭代到无穷小时，实际上没有任何“直线碎片”留在任何地方。相反，回想一下，在构造的每一步中，我们取了 4 个大小为 1/3 的碎片，并重复此操作到无穷小。因此，科赫曲线的分形维数为 D = ln（4）/ln（3） ≈1.262——这不是一个整数！这表明科赫分形在某种程度上不仅仅是一条线，它的无限性有点“推出”到多个维度。

同样，当我们构建谢尔宾斯基三角形时，我们使用了 3 条线的副本，这些线的大小是 1/2。因此，对于谢尔宾斯基三角形，我们有 D = ln（3）/ln（2） ≈1.585。这个数字比科赫曲线大，我们可以直观地看到这种差异——谢尔宾斯基三角形比科赫曲线填充了更多的空间。

五、希尔伯特曲线

现在让我向你展示另一种类型的分形曲线，称为希尔伯特曲线，它是由数学家大卫希尔伯特在1891年发现的。其构建的前几个步骤如下所示：

你可能会注意到，这条曲线似乎以这样一种方式蜿蜒曲折，填满了大量的空间——甚至比谢尔宾斯基三角形还要多，后者有明显的孔洞区域。

那么，希尔伯特曲线的分形维数是多少？

在每个步骤中，我们都使用 4 个大小为 1/2 的部件（以及一点额外的线来连接这些部件）。因此，我们有 D = ln（4）/ln（2） = 2。也就是说，当被拿到无穷小时，希尔伯特曲线实际上是二维的，尽管它是由直线碎片构成的！事实上，当分形被取到无穷小时，它与实心正方形是无法区分的，像这样的曲线被称为空间填充曲线。

我们的朋友龙曲线也是一条空间填充曲线，尽管它填充空间的方式不如希尔伯特曲线的整齐正方形那么直接。再一次，我们可以通过查看 Dragon 曲线的分形维数来看到这一点。在每个步骤中，我们使用 2 个大小为 1/√2 的碎片（或者，每第二步使用 4 个大小为 1/2 的碎片），因此我们得到 D = ln（2）/ln（√2） = 2。
​
为什么你认为分形如此重要？
我不认为它们本身是“重要的”，但有许多自然发生的结构具有类似分形的性质。当然，当你达到原子尺度时，物理世界中的任何事物的细节都会受到限制（这是一件有趣的事情，向你展示了我的意思）。因此，它们只是真正的数学分形的近似值。

其中最明显的是雪花，它们具有分形状的晶体结构。

雷击是另一种自然现象，当闪电从云层中展开，寻找与地面的最佳接触点时，它通常表现出分形性质。这是我看过的最好的慢动作视频之一，它展示了闪电分形的美感。

还有营养丰富的分形！Romanesco 西兰花是可食用（和健康）分形的一个很好的例子。

亚当在左边画了分形西兰花，所以我们认为找到谷歌的版本可能也会有所帮助！

六、还有什么有趣的要补充的吗？

是的，实际上。

之前我谈到了一种生成自相似分形的迭代方法。您可能还记得，我们通过从一条直线开始，将上一次迭代的两个副本彼此成直角放置来构建 Dragon 曲线。事实证明，如果您反复将一张纸对折（沿同一方向折叠），然后展开它，使每次折叠都是直角，这正是您得到的！

这看起来似乎就是一点点构图，画出它们，我们已经搞得一团糟。到处都是钢笔、餐具和纸屑！然而渲染一种自然景观，比如下图：

这就成了电脑构图的另一层境界，总之，分型几何是一个优质资源。