875. 快速幂

题目描述

给定 $n$ 组 $a_i,b_i,p_i$，对于每组数据，求出 $a_i^{b_i}mod{p}_i$ 的值。

输入格式：

第一行包含整数 n。

接下来 n 行，每行包含三个整数 $a_i,b_i,p_i$。

输出格式：

对于每组数据，输出一个结果，表示 $a_i^{b_i}mod{p}_i$ 的值。

每个结果占一行。

数据范围

• $1\le N\le 10^5$
• $1\le a_i,b_i,p_i\le 2\times 10^9$

输入样例

2
3 2 5
4 3 9

输出样例

4
1

方法：快速幂

解题思路

我们用 k 替换 b。
最朴素的做法是，循环 k 次，每次乘 a 再模上 p.
由于这里的 k 比较大，只能另觅他法了。
快速幂的思想就是把 a 的 k 次幂看作是多个 a 的 2 的多少次幂相乘。

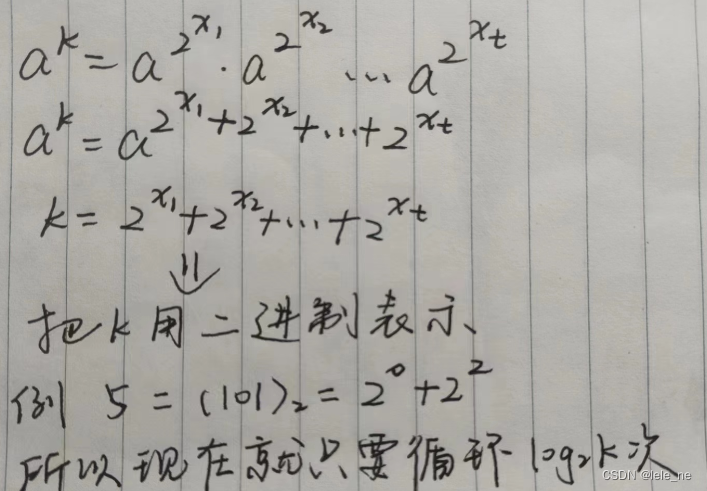
每一次循环，先判断 k 的最后一位是否为 1，如果为 1，则需要把 $res\ast amodp$；
然后将 k 右移 1 位，a 要平方再 mod p
Tips

• 因为这里的数据范围比较大，往往数论的题目都要定义为 long long，不然会爆 int.

代码

#include <iostream>

using namespace std;

typedef long long LL;

int n;

int qmi(int a, int k, int p) {
    int res = 1;
    while(k) {
        if(k & 1)   res = (LL)res * a % p;
        k >>= 1;
        a = (LL)a * a % p;
    }
    return res;
}

int main() {
    cin >> n;
    while(n--) {
        int a, k, p;
        scanf("%d%d%d", &a, &k, &p);
        printf("%d\n", qmi(a, k, p));
    }
    return 0;
}

复杂度分析：

• 时间复杂度：$O(lo{g}_{2}k)$
• 空间复杂度：$O(1)$