数学知识（四）

这一小节讲的是容斥原理和简单博弈论。

容斥原理

定义

最基本的，假设有3个两两相交的圆。那么三个圆所覆盖的面积大小为

$S_1+S_2+S_3-S_1\cap S_2-S_2\cap S_3-S_1\cap S_3+S_1\cap S_2\cap S_3$

如果是2个圆的话，那么其所覆盖的面积为

$S_1+S_2-S_1\cap S_2$

如果是4个圆的话，那么面积为

$S_1+S_2+S_3+S_4$

$-S_1\cap S_2-S_1\cap S_3-S_1\cap S_4-S_2\cap S_3-S_2\cap S_4-S_3\cap S_4$

$+S_1\cap S_2\cap S_3+S_1\cap S_2\cap S_4+S_1\cap S_3\cap S_4+S_2\cap S_3\cap S_4$

$-S_1\cap S_2\cap S_3\cap S_4$

更一般的，假设有 $n$ 个集合，$S_1$，$S_2$，…，$S_n$

这 $n$ 个集合的并集中所包含的元素个数，可以用容斥原理进行计算。

$S_1\cup S_2\cup S_3...\cup S_n={\sum }_i{S}_i-{\sum }_{i,j}{S}_i\cap S_j+{\sum }_{i,j,k}{S}_i\cap S_j\cap S_k-.....$

上式中，包含1个集合的项，一共有 $C_n^1$ 个，包含2个集合的项，一共有 $C_n^2$个；包含3个集合的项，一共有 $C_n^3$ 个，…

所以，上式中的所有项的个数，一共是 $C_n^1+C_n^2+C_n^3+...+C_n^n=2^n-1$，所以上式中一共有 $2^n-1$ 项，时间复杂度是 $2^n$（其实还要看一下每一项的计算复杂度是多少）。

证明

容斥定理要如何来证明呢？我们可以用集合的并操作来考虑。

假设有 n 个集合，每个集合里有一些元素（集合内的元素是不重复的），求这 n 个集合的并集，即求 n 个集合中不同的元素的总个数。根据容斥原理，可以用如下公式进行计算

$S_1\cup S_2\cup S_3...\cup S_n={\sum }_i{S}_i-{\sum }_{i,j}{S}_i\cap S_j+{\sum }_{i,j,k}{S}_i\cap S_j\cap S_k-.....$

现在来证明这个公式的正确性，考虑对于某个元素 x ，其是否只被计数了一次。不妨设这个元素 x 一共在 k 个集合中出现过。那么在上面的公式右侧，只包含一个集合时，x 会被加上 k 次，也就是 $C_k^1$ 次，在第二项，包含2个集合时，x 会被减去上 $C_k^2$ 次，第三项同理，后续的项也同理。

那么 x 被计数的次数就是 $C_k^1-C_k^2+C_k^3-C_k^4+....+(-1{)}^{k-1}\cdot C_k^k$，而这个式子是恒等于1的。所以元素 x 总共只被计数了1次。

$C_k^1-C_k^2+C_k^3-C_k^4+....+(-1{)}^{k-1}\cdot C_k^k$ 这个等式是一个组合恒等式，具体的证明，可以将 $(x+1{)}^n$ 在 $x=-1$ 时进行二项式展开，进行观察。

于是我们就证得，对于任意一个元素 x ，根据容斥原理，其只会被统计一次，也就证明了容斥原理的正确性。

练习题

890. 能被整除的数

给定一个整数 n ，以及m个不同的质数 $p_i$ ，求 1 - n 中能被至少一个质数整除的数有多少个？

举个简单的样例，$n=10，p_1=2，p_2=3$，那么 1 - 10中能被2或3整除的数，有2 3 4 6 8 9 10，共7个

如果暴力来做的话，对于1 - n 每个数，最多可能需要依次枚举 m 个质数，看能否整除，时间复杂度 $O(nm)$，这道题目光 n 就能取到 $10^9$，所以这样做肯定会超时。

用容斥原理来做，首先我们需要定义集合，对于上面的样例数据，我们定义

$S_2$ 表示 1 - 10 中所有能被 2 整除的数，即 $S_2=2,4,6,8,10$，同理，有 $S_3=3,6,9$

我们要求的就是 $S_2\cup S_3=S_2+S_3-S_2\cap S_3=5+3-1=7$

而容斥原理的时间复杂度是 $2^m$ ，对于这道题目，$m$ 最大取到16，所以时间复杂度最多达到 $2^{16}=65536$

我们看一下每一项如何求，即如何求 $S_i$，$S_i$ 包含了 1 - n 中所有 i 的倍数，而我们只用 $S_i$ 表示这个集合中的元素个数，则 $S_i=\lfloor \frac{n}{i}\rfloor$ ，那对于两个集合的交集的个数如何求呢，即 $S_i\cap S_j$，由于给定的数都是质数，则质数两两都是互质的，既能被 i 整除，又能被 j 整除的数，一定是i和j的倍数，那么其最小公倍数是 i × j，则 $S_i\cap S_j=\lfloor \frac{n}{i\cdot j}\rfloor$，对于两个集合的交集，需要2次除法，对于 m 个集合的交集，需要 m 次除法，所以每一项的计算量，我们可以看作是 m ，所以总的复杂度是 $O(2^m\cdot m)$ ，大概是 $2^{16}\cdot 16=2^{20}\approx 10^6$

一共是 $2^m-1$项（容斥原理公式中，其实就是组合数求和，可以按照每一个集合选或不选，进行状态枚举），所以考虑用位运算来做，因为这道题的 m 最大只有 16

#include <iostream>
typedef long long LL;
using namespace std;

const int N = 20;
int p[N]; // 质数

int main() {
	std::ios::sync_with_stdio(false);
	int n, m;
	cin >> n >> m;
	for (int i = 0; i < m; i++) cin >> p[i];
	
	int ans = 0;
	// 状态枚举1 ~ 2^m - 1
	for (int i = 1; i < 1 << m; i++) {
		// 选了多少个集合, 以及计算下质数的乘积
		int cnt = 0, prod = 1;
		for (int j = 0; j < m; j++) {
			if (i >> j & 1) {
				cnt++;
				if ((LL)prod * p[j] > n) {
                    // 乘积超过n了, 说明该项一定为0, 不用计算
					prod = -1;
					break;
				}
				prod *= p[j];
			}
		}
		if (prod != -1) {
			if (cnt & 1) ans += n / prod; // 奇数个集合时，需要加
			else ans -= n / prod; // 偶数个集合时, 需要减
		}
	}
	printf("%d\n", ans);
	return 0;
}

博弈论

Nim游戏

公平组合游戏ICG

若一个游戏满足如下3个条件，则称该游戏为一个公平组合游戏

• 两名玩家交替行动（先手，后手）
• 在游戏进程的任意时刻，可以执行的合法行动，与轮到哪位玩家无关（任意时刻，两名玩家能执行的操作都是相同的）
• 不能行动的玩家判负

像一些常见的棋类游戏，就不是公共组合游戏，比如围棋，五子棋，先手和后手分别只能落黑子和白子，操作是不一样的，胜负的判定也比较复杂。Nim游戏则属于公平组合游戏

有向图游戏

给定一个有向无环图，图中有一个唯一的起点，起点上放一枚棋子，两名玩家交替地把这枚棋子沿着有向边进行移动，每次可以移动一步，无法移动者判负。

任何一个公平组合游戏，都可以转化成一个有向图游戏，具体方法是，将每种局面看成图中的一个点，并且从每个局面，向沿着合法行动能够到达的下一个局面，连一条有向边。（状态机）

先手必胜状态：可以走到某一个必败状态

先手必败状态：走不到任何一个必败状态

练习题：891. Nim游戏

给定 n 堆石子，两名玩家轮流操作，每次操作可以从任意一堆石子中拿走任意数量的石子，最后无法操作的人视为失败。若两人都采用最优策略，问先手是否必胜。

这道题目的结论很简单，把所有石子的数量全部异或起来，如果结果是0，则先手必败；否则先手必胜。可以这样理解，只要某一方操作完，每堆石子的数量一样，那么他必胜。

来证明一下这个结论，首先，终局的状态是所有石子都是0，那么终局的状态的异或结果就是0，遇到终局的那个人必败。我们只需要证明一下，对于某个异或结果不为0的局面，都能走到一个异或结果为0的局面即可。

也就是说，对于某个异或结果不为0的局面，我们都能通过从某堆石子里拿走一部分，使得异或结果变为0。

我们只要证明这一点即可。

设每堆石子的个数为 $a_i$，设所有石子的异或值为 $x$，则有 $a_1\oplus a_2\oplus a_3\oplus ...\oplus a_n=x\ne 0$

假设，$x$ 的二进制表示中，最高的一位1，在第 k 位，则说明，$a_1$ 到 $a_n$ 中，至少存在一个数，其二进制的第 k 位是1（准确的说是存在奇数个数，这些数的二进制表示的第k位都是1）。不妨设这个数为 $a_j$，那么显然有 $a_j\oplus x<a_j$ ，因为 $x$ 的第 k 位是1，且更前面的位全是0，而 $a_j$ 的第 k 位也是1，则这两个数异或起来， $a_j$ 的第 k 位从1变为0，而 $a_j$ 前面更高位都是不变的，而后面更低位可能变成任何数，但是总体来说都是变得更小了。

所以，我们可以从 $a_j$ 中拿走一部分石子，使得其变小，变成 $a_j\oplus x$。

我们看下此时的局面，所有的石子数量异或起来就是 $a_1\oplus a_2\oplus a_3...\oplus a_j\oplus x...\oplus a_n=x\oplus x=0$

所以，对某个异或结果不为0的局面，一定能通过拿走某些石子，使得异或结果变为0。

另外，我们还需要证明下，对于异或结果为0的局面，无论怎么操作，得到的一定是异或结果不为0的局面。

可以用反证法，假设从某个石堆中拿走部分石子，得到的异或结果仍然是0，假设操作的是 $a_j$，操作后该石堆剩余的数量为 $a_j^{{}^{\prime }}$，那么有 $a_1\oplus a_2\oplus ...a_j...\oplus a_n=0$，并且 $a_1\oplus a_2\oplus ...a_j^{{}^{\prime }}...\oplus a_n=0$，把这两个式子异或起来，就有 $a_j\oplus a_j^{{}^{\prime }}=0$，这也就说明 $a_j=a_j^{{}^{\prime }}$，即我们没有从这堆石子中拿走任何石子，显然矛盾了，因为每次操作不能不拿。

总结一下

• 终局（必败状态），异或结果是0
• 异或结果不为0的局面，则一定能通过某个操作，变成异或结果为0的局面
• 异或结果为0的局面，无论如何操作，都会变成异或结果不为0的局面

故，若初始状态异或结果不为0，则先手必胜；否则先手必败。

此题是最简单的nim游戏，可以自行拓展了解 k-nim 游戏

#include <iostream>
using namespace std;

int main() {
	std::ios::sync_with_stdio(false);
	int n, x, res = 0;
	cin >> n;
	while (n--) {
		cin >> x;
		res ^= x;
	}
	if (res) printf("Yes\n");
	else printf("No\n");
	return 0;
}

思考题：892. 台阶-Nim游戏

结论：只需要考虑奇数的台阶数，若奇数的台阶上的石子，异或起来结果不等于0，则先手必胜，否则先手必败。

题解参考这篇

#include <iostream>
using namespace std;

int main() {
	std::ios::sync_with_stdio(false);
	int n, a;
	cin >> n;
	int res = 0;
	for (int i = 1; i <= n; i++) {
		cin >> a;
		if (i & 1) res ^= a;
	}
	if (res) printf("Yes\n");
	else printf("No\n");
	return 0;
}

SG函数

Mex运算

针对集合的一种运算，找到一个集合中不存在的最小的自然数，比如集合 S = {1,2 ,3}，那么Mex(S) = 0

SG函数

对于有向图游戏，我们把每种局面（状态）看成一个点，如果由某个局面，可以转变到另外的一些局面，则我们把这些点之间用有向边连接起来。

我们先将终点的状态的SG函数（没有出边的点），定义为0，假设终点状态为e，则SG(e) = 0，则对于某种状态 x ，其SG函数如何求呢？假设 x 能够转变到 y1，y2，y3，…，yk 。则 SG(X) = Mex{SG(y1), SG(y2), ... , SG(yk)}

如下图所示，每个点的SG函数用红色标注了出来

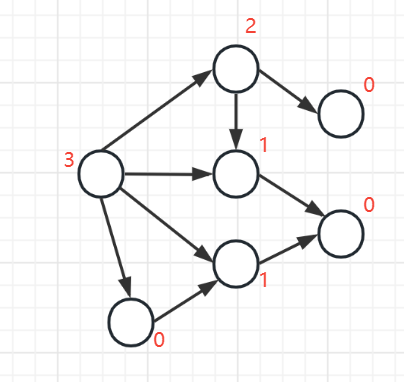
如果整个有向图游戏，只有一个连通块的话，设初始状态为s，则若SG(s) = 0，则先手必败，否则，先手必胜。对于某个状态x，若SG(x) != 0，则说明状态 x 一定能到达某个状态y，并且 SG(y) = 0。所以，任意一个SG非0的状态，都能到达一个SG为0的状态，并且任何一个SG为0的状态，是到不了一个SG为0的状态的。

简单总结就是，任意SG非0的状态，都能到一个SG为0的状态；任意SG为0的状态，都只能到SG非0的状态。而终局状态SG值为0。所以，初始状态SG若非0，则先手必胜，否则先手必败。

若一个图有多个连通块，则我们把每个连通块的初始点的SG值异或起来，若等于0，则先手必败；否则必胜。

证明方法和上面Nim游戏的证明方法一样。

必败态是所有起点的SG值都为0，此时异或结果为0。

若所有起点的SG值异或结果不为0，设所有起点的SG的异或结果为x，则一定能找到一个起点i，使得

SG(i) ^ x < SG(i)，不妨设 y = SG(i) ^ x，则由于y < SG(i)，则说明i一定能到达某个状态j，使得SG(j) = y，那么我们只要从i走到j，那么此时所有连通块起点的异或结果就是

SG(1) ^ SG(2) ^ .. ^ SG(i) ^ x ... SG(n) = x ^ x = 0。

所以一定能从异或结果非0走到0，而从0只能走到非0，于是得证。

通过SG函数，可以显著的降低计算量。

893. 集合-Nim游戏

#include <iostream>
#include <unordered_set>
#include <cstring>
using namespace std;
const int N = 110, M = 10010;
int s[N], f[M];
int k, n;

int sg(int x) {
	if (f[x] != -1) return f[x];
	if (x == 0) return f[x] = 0;
	unordered_set<int> S;
	for (int i = 0; i < k; i++) {
		if (x >= s[i]) S.emplace(sg(x - s[i]));
	}
	for (int i = 0; ; i++) {
		if (!S.count(i)) return f[x] = i;
	}
	return 0;
}

int main() {
	std::ios::sync_with_stdio(false);
	cin >> k;
	for (int i = 0; i < k; i++) cin >> s[i];
	memset(f, -1, sizeof f);
	int res = 0;
	cin >> n;
	for (int i = 0; i < n; i++) {
		int x;
		cin >> x;
		res ^= sg(x);
	}
	if (res) printf("Yes\n");
	else printf("No\n");
	return 0;
}

思考题：894. 拆分 - Nim游戏