文章目录
- [NOIP1996 提高组] 挖地雷
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 思路
- 代码
- 最大食物链计数
- 题目背景
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 思路
- 代码
- [ZJOI2006]三色二叉树
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 思路
- 代码
- 跑路
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 提示
- 数据规模与约定
- 采蘑菇
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 有线电视网
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 思路
- 代码
- 邦邦的大合唱站队
- 题目背景
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 思路
- 代码
- 砝码称重
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 思路
- 代码
- [USACO13NOV]No Change G
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 思路
- 代码
[NOIP1996 提高组] 挖地雷
题目描述
在一个地图上有 N N N个地窖 ( N ≤ 20 ) (N \le 20) (N≤20),每个地窖中埋有一定数量的地雷。同时,给出地窖之间的连接路径。当地窖及其连接的数据给出之后,某人可以从任一处开始挖地雷,然后可以沿着指出的连接往下挖(仅能选择一条路径),当无连接时挖地雷工作结束。设计一个挖地雷的方案,使某人能挖到最多的地雷。
输入格式
有若干行。
第 1 1 1行只有一个数字,表示地窖的个数 N N N。
第 2 2 2行有 N N N个数,分别表示每个地窖中的地雷个数。
第 3 3 3行至第 N + 1 N+1 N+1行表示地窖之间的连接情况:
第 3 3 3行有 n − 1 n-1 n−1个数( 0 0 0或 1 1 1),表示第一个地窖至第 2 2 2个、第 3 3 3个、…、第 n n n个地窖有否路径连接。如第 3 3 3行为 11000 … 0 1 1 0 0 0 … 0 11000…0,则表示第 1 1 1个地窖至第 2 2 2个地窖有路径,至第 3 3 3个地窖有路径,至第 4 4 4个地窖、第 5 5 5个、…、第 n n n个地窖没有路径。
第 4 4 4行有 n − 2 n-2 n−2个数,表示第二个地窖至第 3 3 3个、第 4 4 4个、…、第 n n n个地窖有否路径连接。
… …
第 n + 1 n+1 n+1行有 1 1 1个数,表示第 n − 1 n-1 n−1个地窖至第 n n n个地窖有否路径连接。(为 0 0 0表示没有路径,为 1 1 1表示有路径)。
输出格式
有两行
第一行表示挖得最多地雷时的挖地雷的顺序,各地窖序号间以一个空格分隔,不得有多余的空格。
第二行只有一个数,表示能挖到的最多地雷数。
样例 #1
样例输入 #1
5
10 8 4 7 6
1 1 1 0
0 0 0
1 1
1
样例输出 #1
1 3 4 5
27
提示
【题目来源】
NOIP 1996 提高组第三题
思路
通过题目表述的连通方式,可以建立一棵表示路径的树。
样例所建的树如图:
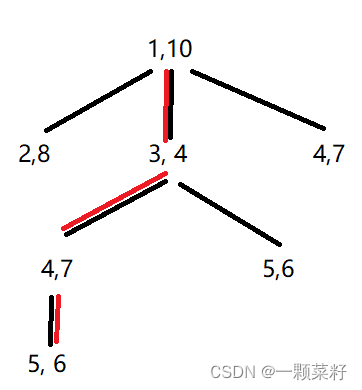
通过如此建树,即可把最多挖地雷数转化为找一条路径上树的节点和最大值。
状态表示f[u] :
集合:表示以u为根节点路径的上的值的集合
属性:max
状态计算:
f[u] = max(f[son] + nums[u])
其实本题就是树形dp的最大路径问题
代码
N = 25 * 25
nums = [0] * 25
st = [False] * 25 # 标记节点是否被遍历过
p = [int(i) for i in range(25)] #存储子节点编号
h = [-1] * N
e = [0] * N
w = [0] * N
ne = [-1] * N
idx = 0
def add(a, b, c) :
global idx
e[idx] = b
w[idx] = c
ne[idx] = h[a]
h[a] = idx
idx += 1
def dfs(u) :
dist = nums[u] #初始化
i = h[u]
while ~ i :
j = e[i]
if dist < dfs(j) + nums[u] :
p[u] = j #记录最优路径的子节点
dist = dfs(j) + nums[u]
i = ne[i]
return dist
def print_path(u) :
print(u, end = " ")
i = p[u]
if i != u :
print_path(i)
n = int(input())
nums[1 : n + 1] = list(map(int, input().split()))
for i in range(1, n) :
tmp = list(map(int, input().split()))
for j in range(len(tmp)) :
if tmp[j] == 1 :
add(i, i + j + 1, nums[i + j + 1])
st[i + j + 1] = True
res = 0
root = 0 # 统计最优路径的根节点
for i in range(1, n + 1) :
if not st[i] :
d = dfs(i)
if res < d:
res = d
root = i
print_path(root)
print()
print(res)
最大食物链计数
题目背景
你知道食物链吗?Delia 生物考试的时候,数食物链条数的题目全都错了,因为她总是重复数了几条或漏掉了几条。于是她来就来求助你,然而你也不会啊!写一个程序来帮帮她吧。
题目描述
给你一个食物网,你要求出这个食物网中最大食物链的数量。
(这里的“最大食物链”,指的是生物学意义上的食物链,即最左端是不会捕食其他生物的生产者,最右端是不会被其他生物捕食的消费者。)
Delia 非常急,所以你只有 1 1 1 秒的时间。
由于这个结果可能过大,你只需要输出总数模上 80112002 80112002 80112002 的结果。
输入格式
第一行,两个正整数 n 、 m n、m n、m,表示生物种类 n n n 和吃与被吃的关系数 m m m。
接下来 m m m 行,每行两个正整数,表示被吃的生物A和吃A的生物B。
输出格式
一行一个整数,为最大食物链数量模上 80112002 80112002 80112002 的结果。
样例 #1
样例输入 #1
5 7
1 2
1 3
2 3
3 5
2 5
4 5
3 4
样例输出 #1
5
提示
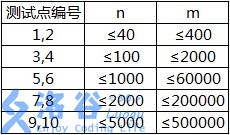
各测试点满足以下约定:
【补充说明】
数据中不会出现环,满足生物学的要求。(感谢 @AKEE )
思路
统计最大食物链数量,最大食物链是图中一条以没有入度的节点为起始点,以没有出度的节点为终点的一条路径。
也即在图上找到入度为0到出度为0节点的路径数量。
理所当然 玄学拓扑序列问题。
在拓扑排序过程中在记录起点到每个节点路径数量,模拟过程如下。
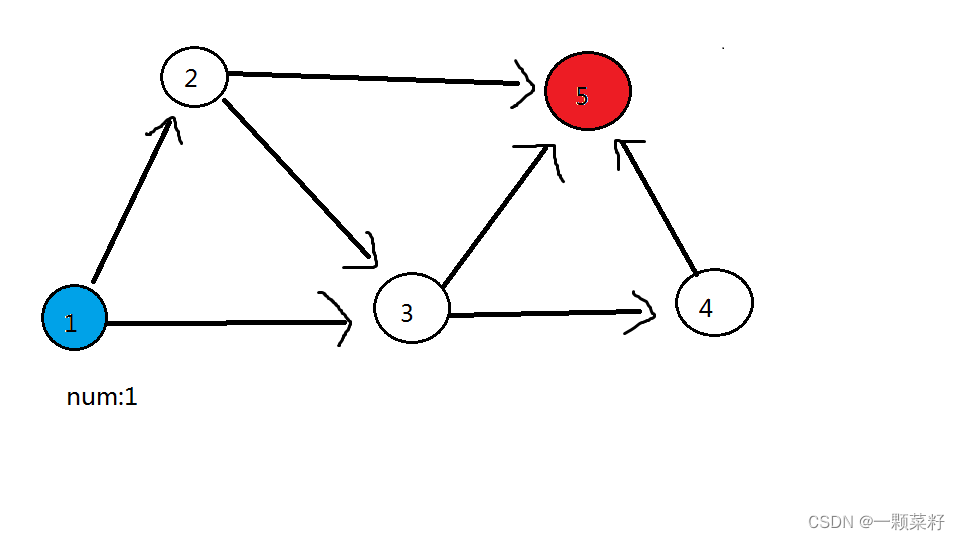
第一轮:删除 1号蓝色点,1 号蓝色点可以到的点(2 号点、3 号点)都加 1
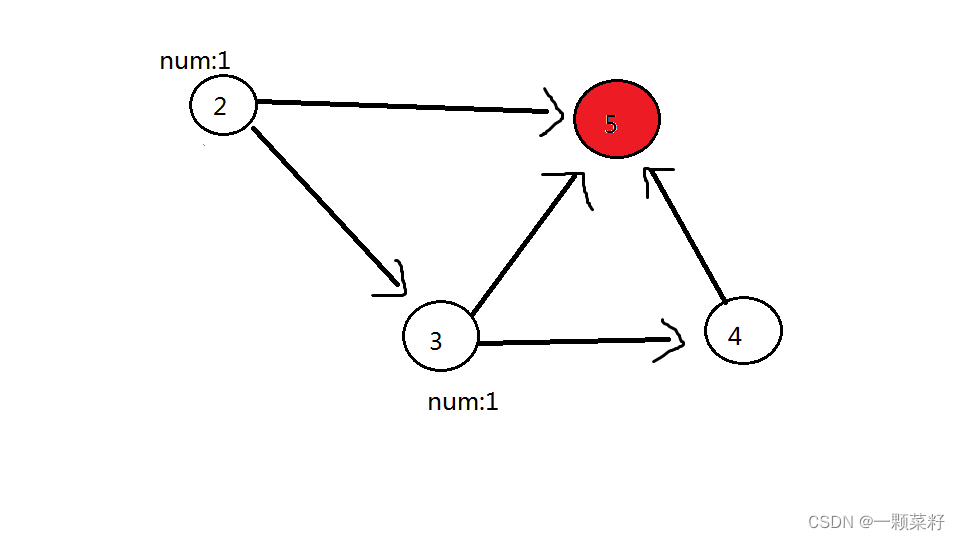
第二轮:删除 2 号点,2 号点可以到的点(3 号点、5 号红色点)都加 1。此时 3 号点答案为 2,5 号点答案为 1
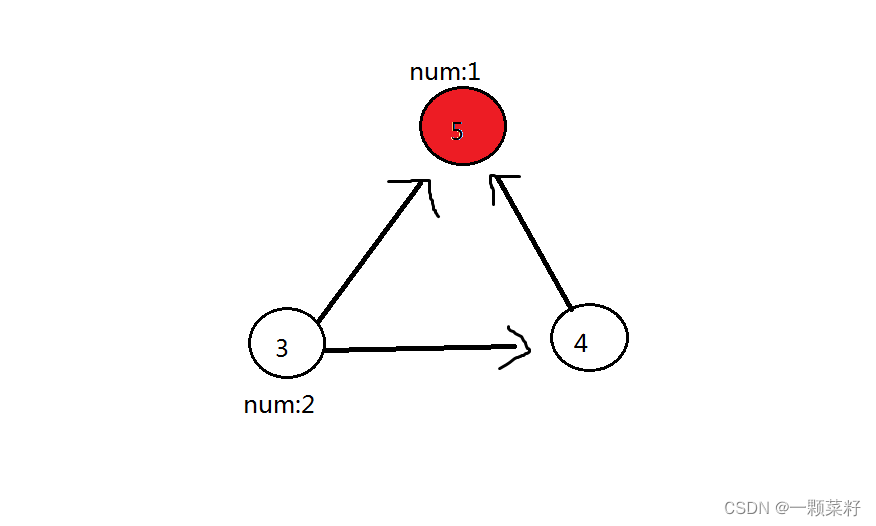
第三轮:删除 3 号点,3 号点可以到的点(4 号点、5 号红色点)都加 2。此时 5 号点答案为 3,4 号点答案为 2

第四轮:最后删除 4 号点,4 号点可以到的点(5 号红色点)加 2,此时 5 号点答案为 5
代码
from collections import deque
N, M = 5010, 500010
MOD = 80112002
h = [-1] * N
e = [0] * M
ne = [-1] * M
idx = 0
st = [0] * N
f = [0] * N
ans = 0
def add(a, b) :
global idx
e[idx] = b
ne[idx] = h[a]
h[a] = idx
idx += 1
def topsort() :
global ans
que = deque()
for i in range(1, n + 1) : #将所有初始节点(入度为0)加入队列
if st[i] == 0 :
que.appendleft(i)
f[i] = 1
while len(que) != 0 :
t = que.pop()
i = h[t]
if i == -1 :
ans = (ans + f[t]) % MOD
while ~ i :
j = e[i]
f[j] = (f[j] + f[t]) % MOD
st[j] -= 1 #减去删去节点入度的边
if st[j] == 0 : # 当删去节点后入度为0则加入队列
que.appendleft(j)
i = ne[i]
n, m = map(int, input().split())
for i in range(m) :
a, b = map(int, input().split())
add(a, b)
st[b] += 1
topsort()
print(ans)
拓扑排序详解请参照这篇拓扑序列
[ZJOI2006]三色二叉树
题目描述
一棵二叉树可以按照如下规则表示成一个由 0 0 0、 1 1 1、 2 2 2 组成的字符序列,我们称之为“二叉树序列 S S S”:
S = { 0 表示该树没有子节点 1 S 1 表示该树有一个节点, S 1 为其子树的二叉树序列 2 S 1 S 2 表示该树由两个子节点, S 1 和 S 2 分别表示其两个子树的二叉树序列 S= \begin{cases} 0& \text表示该树没有子节点\\ 1S_1& 表示该树有一个节点,S_1 为其子树的二叉树序列\\ 2S_1S_2& 表示该树由两个子节点,S_1 和 S_2 分别表示其两个子树的二叉树序列 \end{cases} S=⎩ ⎨ ⎧01S12S1S2表示该树没有子节点表示该树有一个节点,S1为其子树的二叉树序列表示该树由两个子节点,S1和S2分别表示其两个子树的二叉树序列
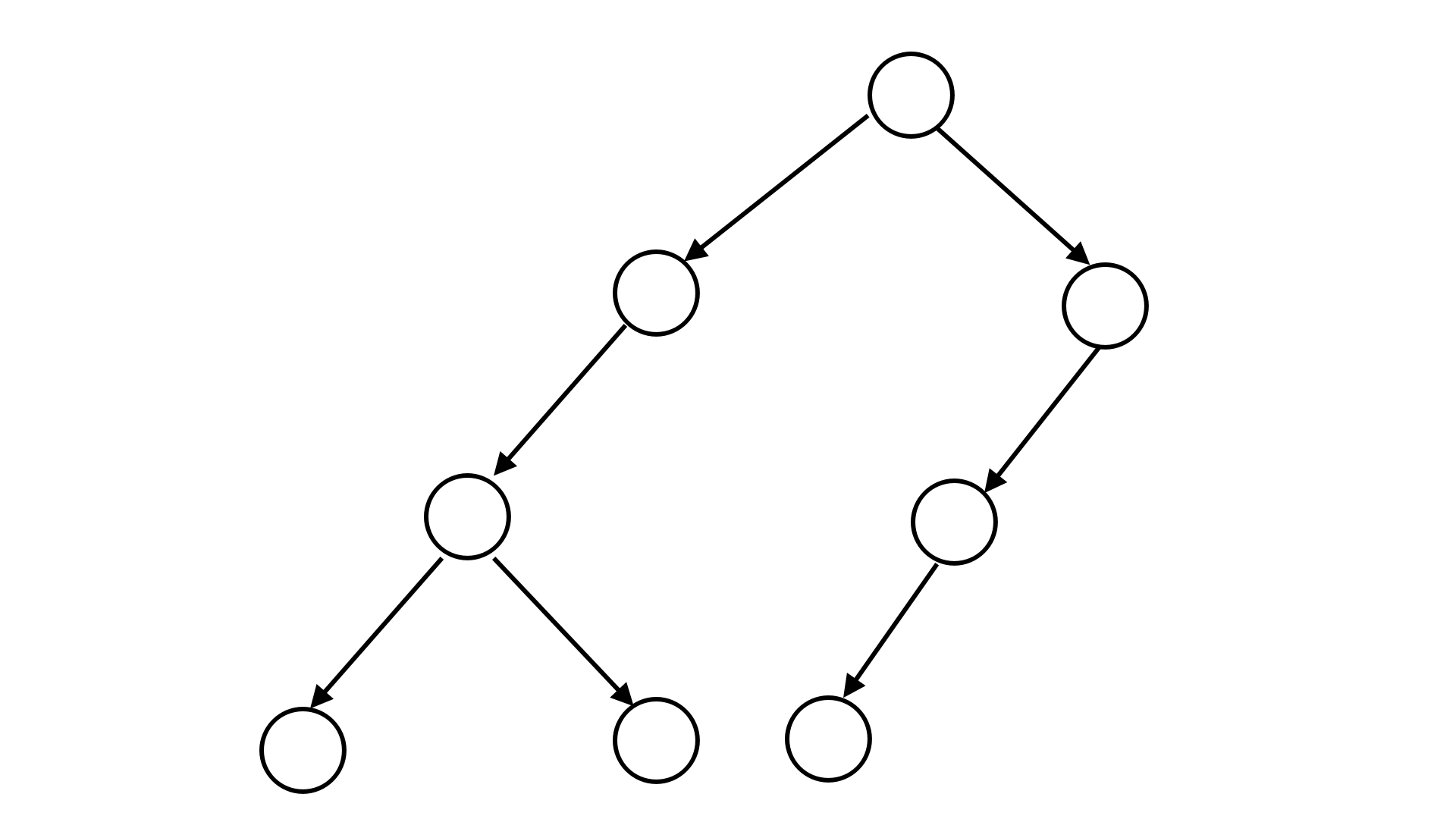
例如,下图所表示的二叉树可以用二叉树序列 S = 21200110 S=\texttt{21200110} S=21200110 来表示。
你的任务是要对一棵二叉树的节点进行染色。每个节点可以被染成红色、绿色或蓝色。并且,一个节点与其子节点的颜色必须不同,如果该节点有两个子节点,那么这两个子节点的颜色也必须不同。给定一颗二叉树的二叉树序列,请求出这棵树中最多和最少有多少个点能够被染成绿色。
输入格式
输入只有一行一个字符串 s s s,表示二叉树序列。
输出格式
输出只有一行,包含两个数,依次表示最多和最少有多少个点能够被染成绿色。
样例 #1
样例输入 #1
1122002010
样例输出 #1
5 2
思路
本题的难点在于建树。
思考对于二叉树序列的遍历方式,可以看出是按照根节点->左节点->右节点的顺序遍历,即先序遍历。
接下来建完树,就是树形dp+状态机问题了
代码
'''
dfs建树:搜索某个根节点的树,如果值为0则为空树,如果值为1,则下一位是其子节点,如果值为2,则下一位和下一位形成的子树后的元素是其子节点
树形dp + 状态机
状态表示 :f[u, 0/1/2], g[u, 0/1/2]
集合:以u为根节点的数,且根染红/green/蓝的情况下,树上染成lu色的节点数量集合
属性:max,min
状态计算:
f[u, 0] += max(f[son, 1], f[son, 2])
f[u, 1] += max(f[son, 0], f[son, 2])
f[u, 2] += max(f[son, 0], f[son, 1])
...
'''
import sys
sys.setrecursionlimit(6000)
N = 500010
h = [-1] * N
e = [0] * N
ne = [-1] * N
idx = 0
f = [[0] * 3 for _ in range(N)]
g = [[0] * 3 for _ in range(N)]
cnt = 0
def add(a, b) :
global idx
e[idx] = b
ne[idx] = h[a]
h[a] = idx
idx += 1
def dfs(u) :
global cnt
cnt += 1
if s[u] == '0' : return
elif s[u] == '1' :
add(u, u + 1)
dfs(u + 1)
elif s[u] == '2' :
add(u, u + 1)
dfs(u + 1)
add(u, cnt)
dfs(cnt)
def dp(u) :
# f[u][1] = 1
# g[u][1] = 1
i = h[u]
son = []
while ~ i :
j = e[i]
son.append(j)
dp(j)
i = ne[i]
if len(son) == 2 :
f[u][0] = max(f[son[0]][1] + f[son[1]][2], f[son[0]][2] + f[son[1]][1])
f[u][1] = max(f[son[0]][0] + f[son[1]][2], f[son[0]][2] + f[son[1]][0]) + 1
f[u][2] = max(f[son[0]][0] + f[son[1]][1], f[son[0]][1] + f[son[1]][0])
g[u][0] = min(g[son[0]][1] + g[son[1]][2], g[son[0]][2] + g[son[1]][1])
g[u][1] = min(g[son[0]][0] + g[son[1]][2], g[son[0]][2] + g[son[1]][0]) + 1
g[u][2] = min(g[son[0]][0] + g[son[1]][1], g[son[0]][1] + g[son[1]][0])
elif len(son) == 1 :
f[u][0] = max(f[son[0]][1], f[son[0]][2])
f[u][1] = max(f[son[0]][0], f[son[0]][2]) + 1
f[u][2] = max(f[son[0]][0], f[son[0]][1])
g[u][0] = min(g[son[0]][1], g[son[0]][2])
g[u][1] = min(g[son[0]][0], g[son[0]][2]) + 1
g[u][2] = min(g[son[0]][0], g[son[0]][1])
else :
f[u][1] = 1
g[u][1] = 1
s = input()
dfs(0)
dp(0)
print(max(f[0][0], f[0][1], f[0][2]), min(g[0][0], g[0][1], g[0][2]))
跑路
题目描述
小 A 的工作不仅繁琐,更有苛刻的规定,要求小 A 每天早上在
6
:
00
6:00
6:00 之前到达公司,否则这个月工资清零。可是小 A 偏偏又有赖床的坏毛病。于是为了保住自己的工资,小 A 买了一个空间跑路器,每秒钟可以跑
2
k
2^k
2k 千米(
k
k
k 是任意自然数)。当然,这个机器是用 longint 存的,所以总跑路长度不能超过 maxlongint 千米。小 A 的家到公司的路可以看做一个有向图,小 A 家为点
1
1
1,公司为点
n
n
n,每条边长度均为一千米。小 A 想每天能醒地尽量晚,所以让你帮他算算,他最少需要几秒才能到公司。数据保证
1
1
1 到
n
n
n 至少有一条路径。
输入格式
第一行两个整数 n , m n,m n,m,表示点的个数和边的个数。
接下来 m m m 行每行两个数字 u , v u,v u,v,表示一条 u u u 到 v v v 的边。
输出格式
一行一个数字,表示到公司的最少秒数。
样例 #1
样例输入 #1
4 4
1 1
1 2
2 3
3 4
样例输出 #1
1
提示
【样例解释】
1 → 1 → 2 → 3 → 4 1 \to 1 \to 2 \to 3 \to 4 1→1→2→3→4,总路径长度为 4 4 4 千米,直接使用一次跑路器即可。
【数据范围】
50 % 50\% 50% 的数据满足最优解路径长度 ⩽ 1000 \leqslant 1000 ⩽1000;
100
%
100\%
100% 的数据满足
n
⩽
50
n \leqslant 50
n⩽50,
m
⩽
10000
m \leqslant 10000
m⩽10000,最优解路径长度
⩽
\leqslant
⩽ maxlongint。
5 2
提示
数据规模与约定
对于全部的测试点,保证
1
≤
∣
s
∣
≤
5
×
1
0
5
1 \leq |s| \leq 5 \times 10^5
1≤∣s∣≤5×105,
s
s
s 中只含字符 0 1 2。
采蘑菇
题目描述
小胖和 ZYR 要去 ESQMS 森林采蘑菇。
ESQMS 森林间有 N N N 个小树丛, M M M 条小径,每条小径都是单向的,连接两个小树丛,上面都有一定数量的蘑菇。小胖和 ZYR 经过某条小径一次,可以采走这条路上所有的蘑菇。由于 ESQMS 森林是一片神奇的沃土,所以一条路上的蘑菇被采过后,又会长出一些新的蘑菇,数量为原来蘑菇的数量乘上这条路的“恢复系数”,再下取整。
比如,一条路上有 4 4 4 个蘑菇,这条路的“恢复系数”为 0.7 0.7 0.7,则第一~四次经过这条路径所能采到的蘑菇数量分别为 4 , 2 , 1 , 0 4,2,1,0 4,2,1,0。
现在,小胖和 ZYR 从 S S S 号小树丛出发,求他们最多能采到多少蘑菇。
输入格式
第一行两个整数, N N N 和 M M M。
第二行到第 M + 1 M+1 M+1 行,每行四个数,分别表示一条小路的起点,终点,初始蘑菇数,恢复系数。
第 M + 2 M+2 M+2 行,一个整数 S S S。
输出格式
一行一个整数,表示最多能采到多少蘑菇,保证答案不超过 ( 2 31 − 1 ) (2^{31}-1) (231−1)。
样例 #1
样例输入 #1
3 3
1 2 4 0.5
1 3 7 0.1
2 3 4 0.6
1
样例输出 #1
8
提示
对于 30 % 30\% 30% 的数据, N ≤ 7 N\le 7 N≤7, M ≤ 15 M\le15 M≤15
另有 30 % 30\% 30% 的数据,满足所有“恢复系数”为 0 0 0。
对于 100 % 100\% 100% 的数据, 1 ≤ N ≤ 8 × 1 0 4 1 \le N\le 8\times 10^4 1≤N≤8×104, 1 ≤ M ≤ 2 × 1 0 5 1\le M\le 2\times 10^5 1≤M≤2×105, 0 ≤ 恢复系数 ≤ 0.8 0\le\text{恢复系数}\le 0.8 0≤恢复系数≤0.8 且最多有一位小数, 1 ≤ S ≤ N 1\le S\le N 1≤S≤N。
tarjan强连通图缩点,鼠鼠学了会儿发现有点难,pass了捏。
有线电视网
题目描述
某收费有线电视网计划转播一场重要的足球比赛。他们的转播网和用户终端构成一棵树状结构,这棵树的根结点位于足球比赛的现场,树叶为各个用户终端,其他中转站为该树的内部节点。
从转播站到转播站以及从转播站到所有用户终端的信号传输费用都是已知的,一场转播的总费用等于传输信号的费用总和。
现在每个用户都准备了一笔费用想观看这场精彩的足球比赛,有线电视网有权决定给哪些用户提供信号而不给哪些用户提供信号。
写一个程序找出一个方案使得有线电视网在不亏本的情况下使观看转播的用户尽可能多。
输入格式
输入文件的第一行包含两个用空格隔开的整数 N N N 和 M M M,其中 2 ≤ N ≤ 3000 2 \le N \le 3000 2≤N≤3000, 1 ≤ M ≤ N − 1 1 \le M \le N-1 1≤M≤N−1, N N N 为整个有线电视网的结点总数, M M M 为用户终端的数量。
第一个转播站即树的根结点编号为 1 1 1,其他的转播站编号为 2 2 2 到 N − M N-M N−M,用户终端编号为 N − M + 1 N-M+1 N−M+1 到 N N N。
接下来的 N − M N-M N−M 行每行表示—个转播站的数据,第 i + 1 i+1 i+1 行表示第 i i i 个转播站的数据,其格式如下:
K A 1 C 1 A 2 C 2 … A k C k K \ \ A_1 \ \ C_1 \ \ A_2 \ \ C_2 \ \ \ldots \ \ A_k \ \ C_k K A1 C1 A2 C2 … Ak Ck
K K K 表示该转播站下接 K K K 个结点(转播站或用户),每个结点对应一对整数 A A A 与 C C C , A A A 表示结点编号, C C C 表示从当前转播站传输信号到结点 A A A 的费用。最后一行依次表示所有用户为观看比赛而准备支付的钱数。单次传输成本和用户愿意交的费用均不超过 10。
输出格式
输出文件仅一行,包含一个整数,表示上述问题所要求的最大用户数。
样例 #1
样例输入 #1
5 3
2 2 2 5 3
2 3 2 4 3
3 4 2
样例输出 #1
2
提示
样例解释
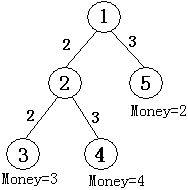
如图所示,共有五个结点。结点 ① 为根结点,即现场直播站,② 为一个中转站,③④⑤ 为用户端,共 M M M 个,编号从 N − M + 1 N-M+1 N−M+1 到 N N N,他们为观看比赛分别准备的钱数为 3 3 3、 4 4 4、 2 2 2。
从结点 ① 可以传送信号到结点 ②,费用为 2 2 2;
也可以传送信号到结点 ⑤,费用为 3 3 3(第二行数据所示);
从结点 ② 可以传输信号到结点 ③,费用为 2 2 2;
也可传输信号到结点 ④,费用为 3 3 3(第三行数据所示)。
如果要让所有用户(③④⑤)都能看上比赛,则信号传输的总费用为: 2 + 3 + 2 + 3 = 10 2+3+2+3=10 2+3+2+3=10,大于用户愿意支付的总费用 3 + 4 + 2 = 9 3+4+2=9 3+4+2=9,有线电视网就亏本了,而只让 ③④ 两个用户看比赛就不亏本了。
思路
- 首先本题抽象为,给定一棵树,每条边都是花费,每个用户节点都是价值,节点之间包含依赖关系,求在保证至少价值为0时,能选取的最大用户节点数。
- 我们能想到的是有依赖的背包问题,给定一棵树,要求包含一定数量的用户节点,求获得的最大价值是多少。
- 转换一下思路,即求以1根节点的树,最大价值至少为0所包含的最大节点数(用户)。
- 先按照,有依赖的背包问题求出f[i, j]以i为根节点,包含j个节点的最大价值。最后枚举根节点为1包含k个节点(用户)的最大价值f[1, k],找到大于等于0的最大的k,答案呼之欲出。
代码
N = 3010
INF = -1000010
h = [-1] * N
e = [0] * N
w = [0] * N
ne = [-1] * N
f = [[INF] * N for _ in range(N)]
c = [0] * N
idx = 0
def add(a, b, c) :
global idx
e[idx] = b
w[idx] = c
ne[idx] = h[a]
h[a] = idx
idx += 1
def dfs(u) :
# 无用户时的最大价值为0
f[u][0] = 0
# 用户节点直接返回
if u > n - m :
f[u][1] = c[u]
return 1
sum = 0
i = h[u]
while ~ i :
ver = e[i]
t = dfs(ver)
sum += t # 更新背包容量为以u为根节点子树包含用户的数量
# 分组背包
for j in range(sum, -1, -1) :
for k in range(1, j + 1) :
f[u][j] = max(f[u][j], f[u][j - k] + f[ver][k] - w[i])
i = ne[i]
return sum
n, m = map(int, input().split())
for i in range(1, n - m + 1) :
tmp = list(map(int, input().split()))
k = tmp[0]
for j in range(k) :
add(i, tmp[2 * j + 1], tmp[2 * j + 2])
c[n - m + 1 : n + 1] = list(map(int, input().split()))
dfs(1)
res = 0
for i in range(1, n + 1) :
if f[1][i] >= 0 :
res = max(res, i)
print(res)
邦邦的大合唱站队
题目背景
BanG Dream!里的所有偶像乐队要一起大合唱,不过在排队上出了一些问题。
题目描述
N个偶像排成一列,他们来自M个不同的乐队。每个团队至少有一个偶像。
现在要求重新安排队列,使来自同一乐队的偶像连续的站在一起。重新安排的办法是,让若干偶像出列(剩下的偶像不动),然后让出列的偶像一个个归队到原来的空位,归队的位置任意。
请问最少让多少偶像出列?
输入格式
第一行2个整数N,M。
接下来N个行,每行一个整数 a i ( 1 ≤ a i ≤ M ) a_i(1\le a_i \le M) ai(1≤ai≤M),表示队列中第i个偶像的团队编号。
输出格式
一个整数,表示答案
样例 #1
样例输入 #1
12 4
1
3
2
4
2
1
2
3
1
1
3
4
样例输出 #1
7
提示
【样例解释】
1 3 √
3 3
2 3 √
4 4
2 4 √
1 2 √
2 2
3 2 √
1 1
1 1
3 1 √
4 1 √
【数据规模】
对于20%的数据, N ≤ 20 , M = 2 N\le 20, M=2 N≤20,M=2
对于40%的数据, N ≤ 100 , M ≤ 4 N\le 100, M\le 4 N≤100,M≤4
对于70%的数据, N ≤ 2000 , M ≤ 10 N\le 2000, M\le 10 N≤2000,M≤10
对于全部数据, 1 ≤ N ≤ 1 0 5 , M ≤ 20 1\le N\le 10^5, M\le 20 1≤N≤105,M≤20
思路
参考
- 首先想一想暴力做法,枚举每个乐队的排列状态,然后根据乐队的排列位置,使原队列中每个所在非正确队列的偶像出队。
- 类似于哈密顿路径,用一个二进制数表示队伍排列情况,1代表排列好了,0表示没排列好。如101表示第1、2个乐队都排列好了。101可由100和001转移而来,转移状态的选择,就相当于选择了乐队排列位置12,21的区别。
- 状态表示:集合:f[i]表示队伍排列状态为i时,偶像出列人数的集合,属性:min,状态计算:
f [ i ] = m i n ( f [ i x o r 2 j ] + j 乐队区间内非 j 乐队偶像出列人数 ) f[i] = min(f[i \ xor \ 2^j] + j乐队区间内非j乐队偶像出列人数) f[i]=min(f[i xor 2j]+j乐队区间内非j乐队偶像出列人数),这里j必须是i状态队伍中存在的排列好的乐队。
j 乐队区间内非 j 乐队偶像出列人数 j乐队区间内非j乐队偶像出列人数 j乐队区间内非j乐队偶像出列人数 = j 乐队偶像人数 − j 乐队区间在原队伍内 j 乐队偶像人数 j乐队偶像人数 - j乐队区间在原队伍内j乐队偶像人数 j乐队偶像人数−j乐队区间在原队伍内j乐队偶像人数
= n u m s [ j ] − ( s u m [ l e n ] [ j ] − s u m [ l e n − n u m s [ j ] ] [ j ] ) nums[j] - (sum[len][j] - sum[len - nums[j]][j]) nums[j]−(sum[len][j]−sum[len−nums[j]][j])。nums表示j乐队偶像总人数,
sum表示原队伍中1~len区间内j偶像人数的前缀和。
代码
N = 22
M = 1 << N
INF = 100010
f = [INF] * M
nums = [0] * N
sumary = [[0] * N for _ in range(INF)]
n, m = map(int, input().split())
for i in range(1, n + 1) :
a = int(input())
nums[a] += 1 # 统计乐队偶像个数
for j in range(1, m + 1) : # 求每个乐队人数的前缀和
sumary[i][j] = sumary[i - 1][j]
sumary[i][a] += 1
f[0] = 0 # 状态为0是没有人出列
for i in range(1, 1 << m) :
length = 0
for j in range(m) : # 统计状态下以排好队列的长度
if i & (1 << j) : length += nums[j + 1]
for j in range(m) :
if i & (1 << j) : # 如果存在已排好乐队
f[i] = min(f[i], f[i ^ (1 << j)] + nums[j + 1] - (sumary[length][j + 1] - sumary[length - nums[j + 1]][j + 1]))
print(f[(1 << m) - 1])
砝码称重
题目描述
现有 n n n 个砝码,重量分别为 a i a_i ai,在去掉 m m m 个砝码后,问最多能称量出多少不同的重量(不包括 0 0 0)。
请注意,砝码只能放在其中一边。
输入格式
第 1 1 1 行为有两个整数 n n n 和 m m m,用空格分隔。
第 2 2 2 行有 n n n 个正整数 a 1 , a 2 , a 3 , … , a n a_1, a_2, a_3,\ldots , a_n a1,a2,a3,…,an,表示每个砝码的重量。
输出格式
仅包括 1 1 1 个整数,为最多能称量出的重量数量。
样例 #1
样例输入 #1
3 1
1 2 2
样例输出 #1
3
提示
【样例说明】
在去掉一个重量为 2 2 2 的砝码后,能称量出 1 , 2 , 3 1, 2, 3 1,2,3 共 3 3 3 种重量。
【数据规模】
对于 20 % 20\% 20% 的数据, m = 0 m=0 m=0。
对于 50 % 50\% 50% 的数据, m ≤ 1 m\leq 1 m≤1。
对于 50 % 50\% 50% 的数据, n ≤ 10 n\leq 10 n≤10。
对于 100 % 100\% 100% 的数据, n ≤ 20 n\leq 20 n≤20, m ≤ 4 m\leq 4 m≤4, m < n m < n m<n, a i ≤ 100 a_i\leq 100 ai≤100。
思路
- 题意理解,在n个砝码的m的组合中,求组合中最多能称出多少不同重量。
- 首先,求n个砝码的m个砝码的组合(不可重复),可以使用dfs。
- 其次是求在m个砝码,可以称出多少不同重量。可以转化为m个砝码是否可以称出k的重量,枚举k的数量,即为不同重量。
- 转化为背包问题bool f[i, j],表示前i个物品中选,是否可以表示j体积。f[i, j] = f[i - 1, j - nums[i]]
代码
N = 25
st = [False] * N
ans = 0
p = []
def dfs(start) : # 求不重组合数
if len(p) == n - m : # 终止条件
dp()
return
if cur >= n : # 合法性优化
return
for i in range(start, n) :
if i - 1 >= 0 and w[i - 1] == w[i] and not st[i - 1] : continue # 等效冗余优化
p.append(w[i])
st[i] = True
dfs(i + 1)
p.pop()
st[i] = False
def dp() : #0-1背包模板
global ans
f = [False] * (n * 100 + 1)
f[0] = True
sum, cnt = 0, 0
for i in range(n - m) :
sum += p[i]
for j in range(sum, p[i] - 1, -1) :
if f[j - p[i]] and not f[j] :
cnt += 1
f[j] = True
ans = max(ans, cnt)
n, m = map(int, input().split())
w = list(map(int, input().split()))
w.sort()
dfs(0, 0)
print(ans)
[USACO13NOV]No Change G
题目描述
Farmer John is at the market to purchase supplies for his farm. He has in his pocket K coins (1 <= K <= 16), each with value in the range 1…100,000,000. FJ would like to make a sequence of N purchases (1 <= N <= 100,000), where the ith purchase costs c(i) units of money (1 <= c(i) <= 10,000). As he makes this sequence of purchases, he can periodically stop and pay, with a single coin, for all the purchases made since his last payment (of course, the single coin he uses must be large enough to pay for all of these). Unfortunately, the vendors at the market are completely out of change, so whenever FJ uses a coin that is larger than the amount of money he owes, he sadly receives no changes in return!
Please compute the maximum amount of money FJ can end up with after making his N purchases in sequence. Output -1 if it is impossible for FJ to make all of his purchases.
约翰到商场购物,他的钱包里有K(1 <= K <= 16)个硬币,面值的范围是1…100,000,000。
约翰想按顺序买 N个物品(1 <= N <= 100,000),第i个物品需要花费c(i)块钱,(1 <= c(i) <= 10,000)。
在依次进行的购买N个物品的过程中,约翰可以随时停下来付款,每次付款只用一个硬币,支付购买的内容是从上一次支付后开始到现在的这些所有物品(前提是该硬币足以支付这些物品的费用)。不幸的是,商场的收银机坏了,如果约翰支付的硬币面值大于所需的费用,他不会得到任何找零。
请计算出在购买完N个物品后,约翰最多剩下多少钱。如果无法完成购买,输出-1
输入格式
* Line 1: Two integers, K and N.
* Lines 2…1+K: Each line contains the amount of money of one of FJ’s coins.
* Lines 2+K…1+N+K: These N lines contain the costs of FJ’s intended purchases.
输出格式
* Line 1: The maximum amount of money FJ can end up with, or -1 if FJ cannot complete all of his purchases.
样例 #1
样例输入 #1
3 6
12
15
10
6
3
3
2
3
7
样例输出 #1
12
提示
FJ has 3 coins of values 12, 15, and 10. He must make purchases in sequence of value 6, 3, 3, 2, 3, and 7.
FJ spends his 10-unit coin on the first two purchases, then the 15-unit coin on the remaining purchases. This leaves him with the 12-unit coin.
思路
- 首先本题和金币使用顺序有关,所以是个集合顺序类状压dp。
- 考虑状态:集合dp[i]表示用i状态下的硬币能购买到的商品集合,属性max,f[i]表示i状态下的花费。状态转移: d p [ i ] = m a x ( d p [ i x o r 2 j ] + i x o r 2 j 状态能买到的商品开始,用 j 硬币可以买到的商品个数 ) dp[i] = max(dp[i \ xor\ 2^j ] + i\ xor\ 2^j状态能买到的商品开始,用j硬币可以买到的商品个数) dp[i]=max(dp[i xor 2j]+i xor 2j状态能买到的商品开始,用j硬币可以买到的商品个数)
代码
N = 17
M = 100010
ans = 6790000010
dp, f = [0] * (1 << N), [0] * (1 << N)
sumary, pay, c= [0] * M, [0] * M, [0] * M
# 查找小于等于target数中最大的一个数的位置
def check(target, st) :
l, r = st, n
while l < r :
mid = (l + r + 1) >> 1
if sumary[mid] - sumary[st - 1] <= target :
l = mid
else : r = mid - 1
return l
m, n = map(int, input().split())
tot = 0
for i in range(1, m + 1) :
c[i] = int(input())
tot += c[i] # 记录总金币数量
for i in range(1, n + 1) :
pay[i] = int(input())
sumary[i] = sumary[i - 1] + pay[i] # 记录商品价格前缀和
for i in range(1, 1 << m) :
for j in range(m) :
if i & (1 << j) :
x = i ^ (1 << j)
s = check(c[j + 1], dp[x] + 1)
if s > dp[i] :
dp[i] = s
f[i] = f[x] + c[j + 1]
if dp[i] == n : ans = min(f[i], ans)
print(max(tot - ans, -1))








![[leetcode.29]两数相除,位运算虽好,不要满眼是她](https://img-blog.csdnimg.cn/fcea493452824a338527b027965da147.png)