目前小波分析算法常采用Mallat快速算法。该算法由与滤波器卷积、隔点采样和隔点插零等三个环节组成。由于实际使用的滤波器并不具有理想频域特性，使得在标准二进小波算法中存在着频率混叠和小波系数失真等缺点，在标准二进小波包算法中还存在频带错乱现象。针对标准二进小波(包)算法的不足，不少学者进行了深入研究。

有学者采用Grey编码对错乱的频带进行重新排序，以消除小波包变换算法中的频带错乱现象，但是这种排序法并未解决引起频带错乱的根本问题，针对其不足，学者提出小波包的移频算法来解决小波包分析中的频带错位现象。移频算法的实质是在隔点采样之前对经高通滤波器得到的高频分量作移频处理，从而使分量中的最高频率降低以满足采样定理，避免频率混叠。这种移频算法虽然在一定程度上能解决小波变换过程中高频子带部分的频率混叠问题，但是由于低通、高通滤波器都不是锐截止，两者存在频带交错，移频算法对于低频子带中出现的本属于高频子带分量无法进行处理，因此没有彻底解决频率混叠现象。有学者在对小波分解过程中存在频率混叠的原因进行分析的基础上，提出一种改进的算法以克服频率混叠现象，并将这种改进的方法引入到小波包变换算法中，克服小波包变换中的频率混叠。有学者提出基于新增的校正滤波器的改进算法。其实质是在隔点采样以及隔点插值之前，通过纠正滤波器将相应频段之外的频谱全部置零，从而消除频率混叠现象。采用该方法在一定程度上可以消除频率混叠现象，但是该方法存在一定的不足：由于没有解决高频段在隔点采样时出现的因采样频率不满足采样定理而导致的混叠现象，使得重构后的各频段不再是按顺序排列，而且该算法中的纠正滤波器通过引入傅里叶变换来消除由于小波滤波器非理想频域截止性产生的频率混叠成分会造成幅值、相位失真和变换不可逆，不再满足完全重构条件。有学者通过对标准小波包算法中单支重构时出现的频率混叠和幅值失真现象进行分析，提出通过对传统小波滤波器的过渡段进行曲线拟合进而设计一个新的纠正滤波器的方法来消除频率混叠及幅值失真。算法中对传统滤波器过渡段的曲线拟合是针对特定小波进行，拟合点函数值是通过估算的方法近似确定，因而该算法的通用性及可操作性存在不足。有学者从理论上定量分析了小波变换过程中由于滤波器的频带交错造成的能量泄漏，提出一种基于重采样的小波改进算法以减少能量泄漏。其具体做法就是通过对信号进行重新采样，使得感兴趣的频段不在小波滤波器交错段，进而提高该频段分析精度。该方法需要预先确定感兴趣的频段，且同时需关注的频段数较少，否则该方法将无效。

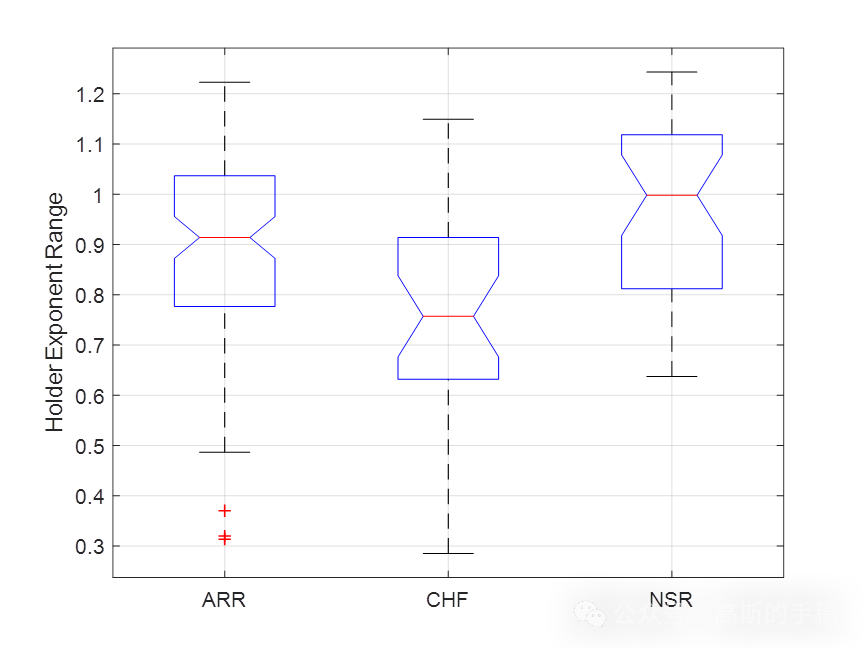
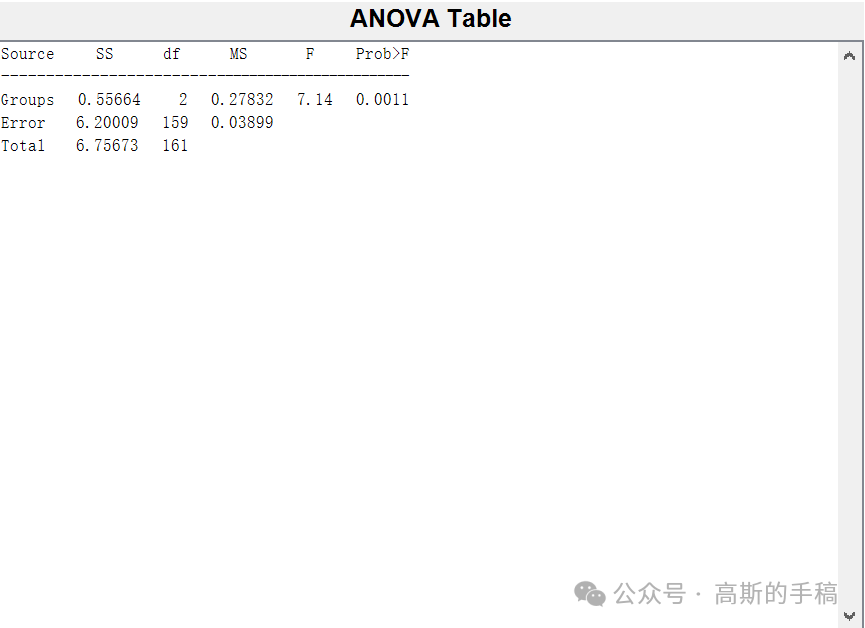
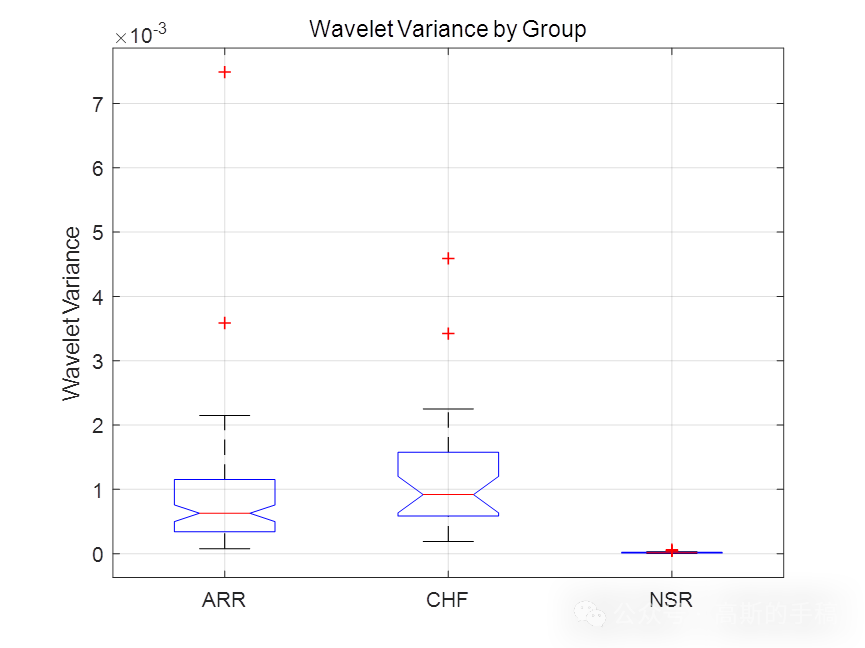
鉴于此，采用最大重叠离散小波包特征提取和支持向量机对ECG心电信号进行分类，所提取的特征为4阶自回归模型（AR）系数，小波包香农熵和奇异谱多重分形小波估计特征，运行环境为MATLAB 2018A。

function arcfs = blockAR(x,order,numbuffer)
numwindows = numel(x)/numbuffer;
y = buffer(x,numbuffer);
arcfs = zeros(order,size(y,2));
for kk = 1:size(y,2)
    artmp =  arburg(y(:,kk),order);
    arcfs(:,kk) = artmp(2:end);
end
arcfs = reshape(arcfs,order*numwindows,1);
arcfs = arcfs';
完整代码可通过知乎学术咨询获得：
https://www.zhihu.com/consult/people/792359672131756032?isMe=1
end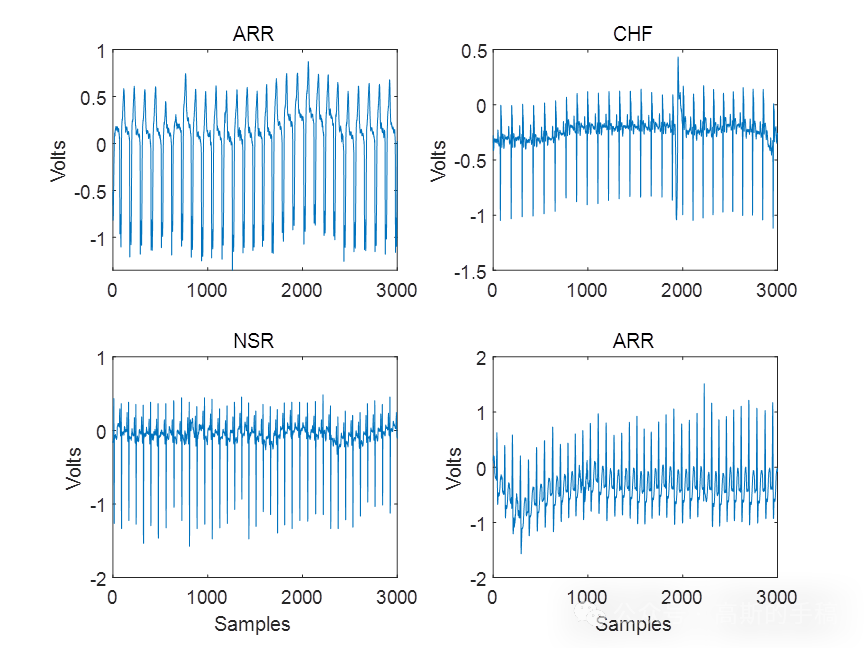

工学博士，担任《Mechanical System and Signal Processing》《中国电机工程学报》《控制与决策》等期刊审稿专家，擅长领域：现代信号处理，机器学习，深度学习，数字孪生，时间序列分析，设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。