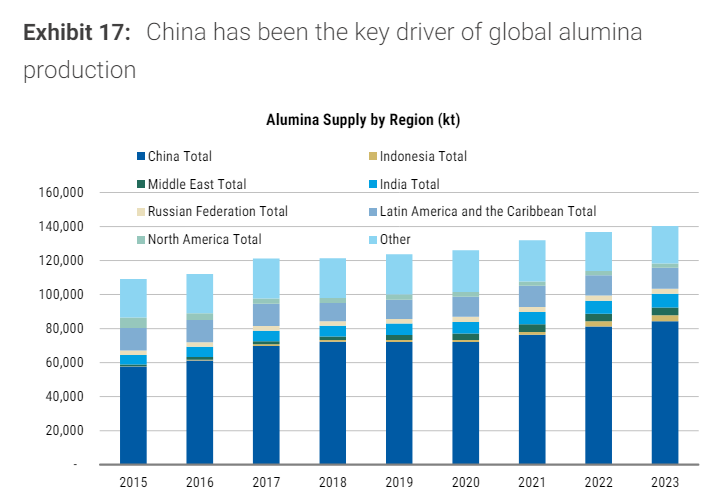
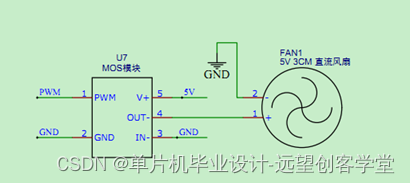
题目:
from Crypto.Util.number import *
from secret import flag
m = bytes_to_long(flag)
n = 1
for i in range(15):
n *=getPrime(32)
e = 65537
c = pow(m,e,n)
print(f'n = {n}')
print(f'c = {c}')
n = 15241208217768849887180010139590210767831431018204645415681695749294131435566140166245881287131522331092026252879324931622292179726764214435307
c = 12608550100856399369399391849907846147170257754920996952259023159548789970041433744454761458030776176806265496305629236559551086998780836655717
题目叫yafu,我们知道yafu是用来分解大素数的,故我们将n分解。
法一:我们可以采用在线网站分解factordb.com
分解之后我们直接将挨个输如到EXP中,然后计算phi:(p1-1)*(p2-1)*....*(pn-1).最后正常解出即可。
法二:我们使用python脚本分解
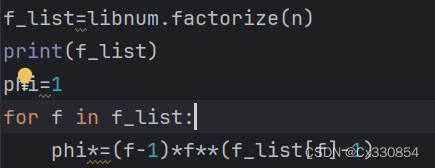
f_list=libnum.factorize(n)
输出结果如下![]()
冒号前的数是分解出来的素数,第二个数是该数出现的次数。
然后我们利用欧拉函数计算phi:若n = p^k,其中 p 是质数,k 是正整数,那么 φ(n) = p^(k-1) * (p-1)。当出现次数为1时,即k=1,p^(k-1)=1.与一般式同
EXP:
from Cryptodome.Util.number import *
import libnum
from gmpy2 import gmpy2
e = 65537
n = 15241208217768849887180010139590210767831431018204645415681695749294131435566140166245881287131522331092026252879324931622292179726764214435307
c = 12608550100856399369399391849907846147170257754920996952259023159548789970041433744454761458030776176806265496305629236559551086998780836655717
f_list=libnum.factorize(n)
print(f_list)
phi=1
for f in f_list:
phi*=(f-1)*f**(f_list[f]-1)
d=gmpy2.invert(e,phi)
print(long_to_bytes(pow(c,d,n)))
![[vue3后台管理二]首页和登录测试](https://img-blog.csdnimg.cn/direct/dba3a7b2120b4b36be69931ff1a413a2.png)