算法思路介绍:
费舍尔线性判别分析(Fisher's Linear Discriminant Analysis,简称 LDA),用于将两个类别的数据点进行二分类。以下是代码的整体思路:
-
生成数据:
- 使用
randn函数生成随机数,构建两个类别的合成数据点。 - 第一个类别的数据点分布在以 (2,2) 为中心的正态分布中。
- 第二个类别的数据点分布在以 (-2,-2) 为中心的正态分布中。
- 使用
-
计算类别均值和散布矩阵:
- 计算每个类别的数据点的均值(类别中心)。
- 计算每个类别的散布矩阵(类别内离散度矩阵)。
-
计算费舍尔线性判别:
- 计算费舍尔判别向量 W,它是使类间散布与类内散布的比值最大化的向量。
- 计算类内散布矩阵的总和
Sw。 - 利用线性代数中的求逆和乘法,计算出判别向量 W。
-
生成测试样本 (x):
使用randn函数生成一个随机测试样本。 -
对测试样本进行分类:
将测试样本投影到判别向量 W 上,并与预先设定的阈值比较以进行分类。 -
绘图:
- 绘制两个类别的数据点,以红色和蓝色表示。
- 标记测试样本点,并根据分类结果用不同的颜色表示。
- 绘制费舍尔判别线,表示分类的决策边界。
- 绘制判别线上的阈值点。
- 绘制测试样本在判别线上的投影点,并画出测试样本与其投影点之间的连线。
通过这些步骤,代码能够实现费舍尔线性判别分析,并对新的测试样本进行分类和可视化。
部分代码:
m1=mean(X(1:N,:));
m2=mean(X(N+1:2*N,:));
S1=0;S2=0;
for i=1:N
S1=S1+(X(i,:)-m1)*(X(i,:)-m1)';
end
for i=N+1:2*N
S1=S1+(X(i,:)-m1)*(X(i,:)-m1)';
end
Sw=S1+S2;
W=inv(Sw)*(m1-m2);
W=W./norm(W)
% ====================================================================
x=randn(1,2);%待判样本
y0=W*(m1+m2)'/2;
if W*x'>y0
disp('待判样本属于第一类')
hold on,plot(x(1),x(2),'r+','MarkerSize',10,'LineWidth',2)
else
disp('待判样本属于第二类')
hold on,plot(x(1),x(2),'b+','MarkerSize',10,'LineWidth',2)
end
legend('Cluster 1','Cluster 2','x','Location','NW')
% =================画投影直线=====================
X1=-8:0.05:8;
X2=(W(2)/W(1))*X1-6;
hold on,plot(X1,X2,'k','LineWidth',2);
% ================求投影直线上的阈值点============
x0=W(1)*(y0)/W(2);
y0=W(2)^2*y0-6*W(1)^2+W(1)*W(2)*x0;
x0=(y0+6)*W(1)/W(2);
hold on,plot(x0,y0,'ro','MarkerSize',10);
% =============求待判样本在投影直线上的投影点==============
y1=W(1)^2*x(1)+6*W(1)*W(2)+W(1)*W(2)*x(2);
y2=W(2)/W(1)*y1-6;
hold on,plot(y1,y2,'r.','MarkerSize',30);
hold on,plot([x(1) y1],[x(2) y2],'g','LineWidth',2);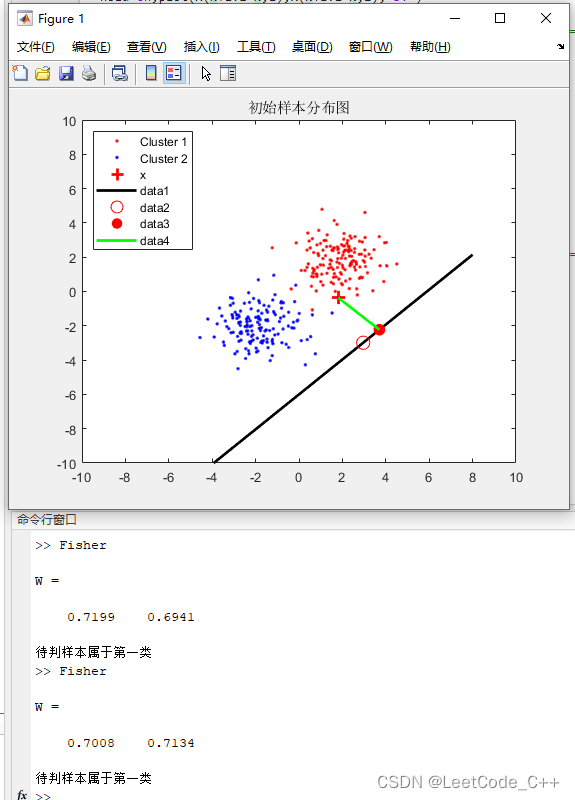




![[LitCTF 2023]yafu (中级) (素数分解)](https://img-blog.csdnimg.cn/direct/71f4ed8317ab4e829f089146738cffe0.png)
![[vue3后台管理二]首页和登录测试](https://img-blog.csdnimg.cn/direct/dba3a7b2120b4b36be69931ff1a413a2.png)