题目描述

现有一棵由 n 个节点组成的无向树，节点编号从 0 到 n - 1 ，共有 n - 1 条边。

给你一个二维整数数组 edges ，长度为 n - 1 ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条边。另给你一个整数数组 restricted 表示 受限 节点。

在不访问受限节点的前提下，返回你可以从节点 0 到达的 最多 节点数目。

注意，节点 0 不 会标记为受限节点。

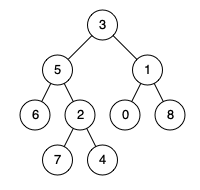
示例 1：

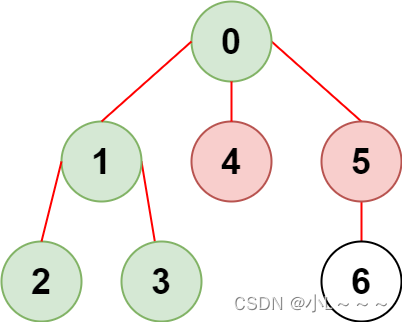
输入：n = 7, edges = [[0,1],[1,2],[3,1],[4,0],[0,5],[5,6]], restricted = [4,5]
输出：4
解释：上图所示正是这棵树。
在不访问受限节点的前提下，只有节点 [0,1,2,3] 可以从节点 0 到达。

示例 2：

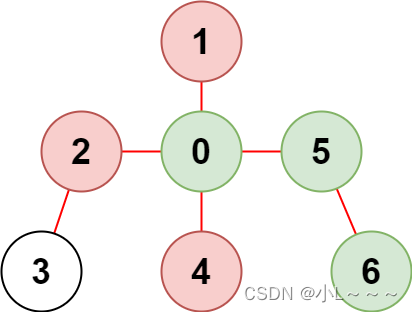
输入：n = 7, edges = [[0,1],[0,2],[0,5],[0,4],[3,2],[6,5]], restricted = [4,2,1]
输出：3
解释：上图所示正是这棵树。
在不访问受限节点的前提下，只有节点 [0,5,6] 可以从节点 0 到达。

解题思路

首先建好图，然后进行无重复访问的 BFS（广度优先搜索），然后设立一个visited数组，被限制的结点和已访问过的结点则标记好不用访问即可。

AC代码

class Solution {
public:
    bool visited[200000] = {false};
    int reachableNodes(int n, vector<vector<int>>& edges, vector<int>& restricted) {
       int ans = 0;
       queue<int>q;
       for(auto i : restricted) visited[i] = true;
       vector<int>G[200000], a;
       for(int i = 0; i < edges.size(); i++) {
           a = edges[i];
           G[a[0]].push_back(a[1]);
           G[a[1]].push_back(a[0]);
       }
    //    for(int i = 0; i < n; i++) {
    //        cout << "i=" << i << " ";
    //        for(auto j : G[i]) cout << j << " ";
    //        cout << endl;
    //    }
       q.push(0);
       while(!q.empty()) {
           int top = q.front();
           q.pop();
           for(auto i : G[top]) {
               if(visited[i]) continue;
                q.push(i);
                ans++;
                visited[i] = true;
           }
       }
       return ans == 0 ? 1 : ans; // 如果根节点和其他任何结点都有限制则返回1
    }
};