文章目录
- 多元线性回归
- 多元线性回归公式推导
- 举例:波士顿房价
- 取特征值RM为例
- 取所有特证为例
多元线性回归
多元线性回归方程:特征值为两个或两个以上。
以下是多元线性回归的模型,我们需要求出theta,使得真实值和预测值的差值最小。
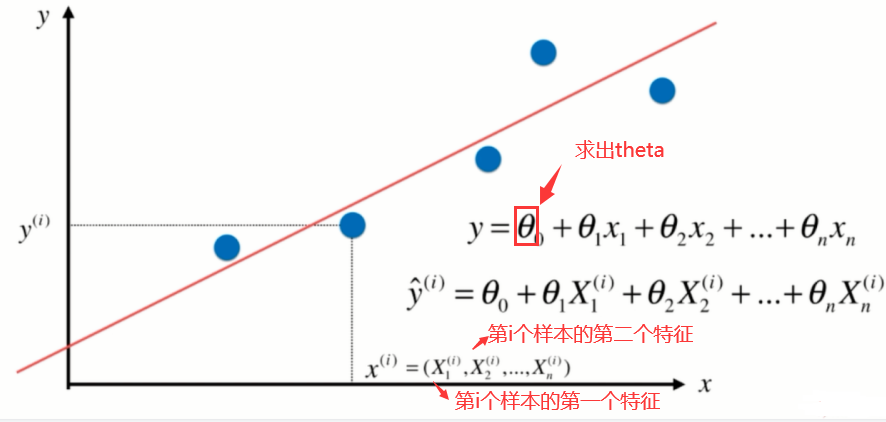
多元线性回归公式推导

通过对矩阵进行转换,加一个X0维度,可以求出两个矩阵点乘的最小值问题。
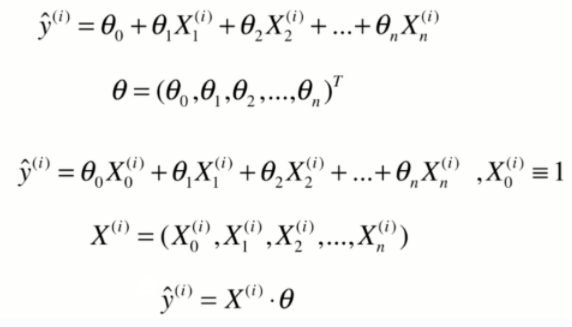
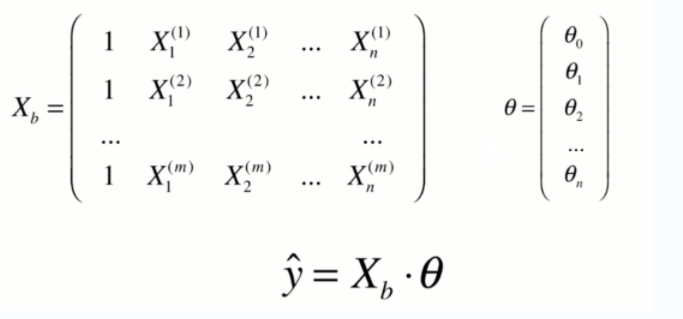

西塔0(theta)代表截距,西塔除第一个以外的元素代表系数。
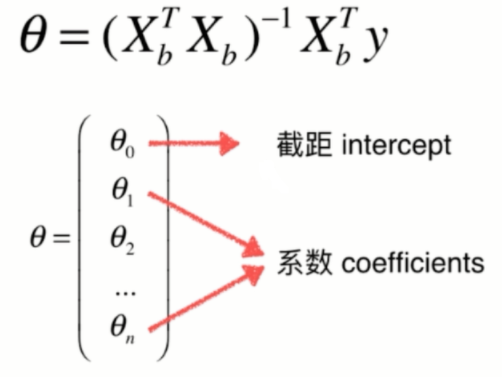
正规方程解的优点:不需要对数据进行归一化处理。
正规方程解的缺点:时间复杂度高,是O(n^3)。
举例:波士顿房价
取特征值RM为例
- 先获取数据
from sklearn.datasets import load_boston
boston = load_boston()
x = boston.data[:,5] # 获取所有行第6列的数据
y = boston.target
x = x[y<50] # 取房价小于50的下标,在x中获取对应的下标值
y = y[y<50]
- 打印数据的描述,查看数据特征,以RM房间数量特征为例

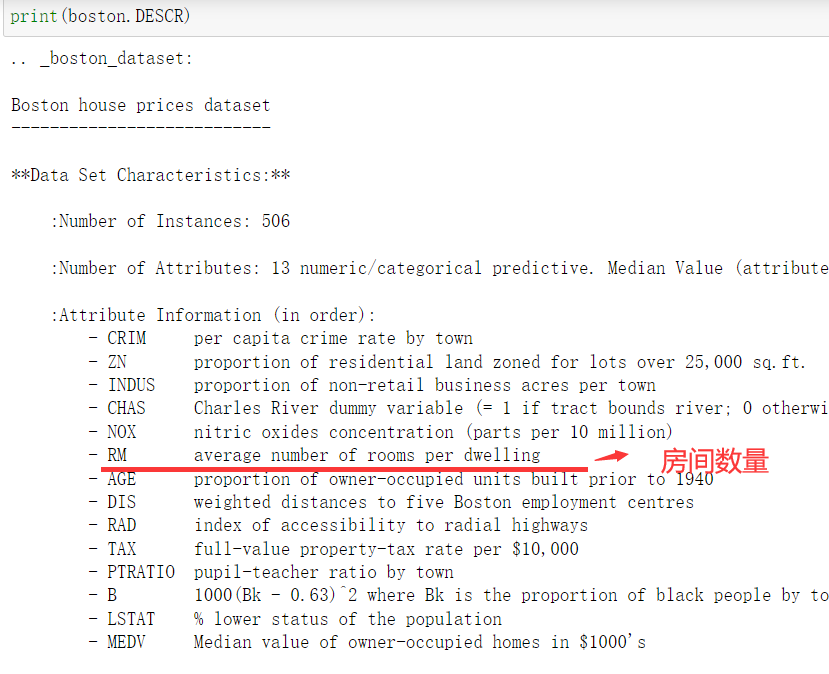
- 获取线性回归训练模型
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
X_train,X_test,y_train,y_test = train_test_split(x,y)
lin_reg = LinearRegression()
lin_reg.fit(X_train.reshape(-1,1),y_train)

- 画出散点图和线性回归模型
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.plot(x, lin_reg.predict(x.reshape(-1,1)), color='r')
plt.scatter(x,y)
plt.xlabel('房间数量')
plt.ylabel('房价')
plt.show()
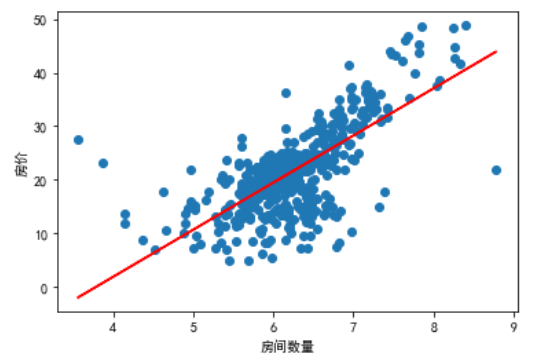
取所有特证为例
- 获取数据
from sklearn.datasets import load_boston
boston = load_boston()
x = boston.data
y = boston.target
X = x[y<50]
y1 = y[y<50]

- 对数据进行处理,使用线性回归算法,训练模型
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
X_train,X_test,y_train,y_test = train_test_split(X,y1)
lin_reg = LinearRegression()
lin_reg.fit(X_train,y_train)
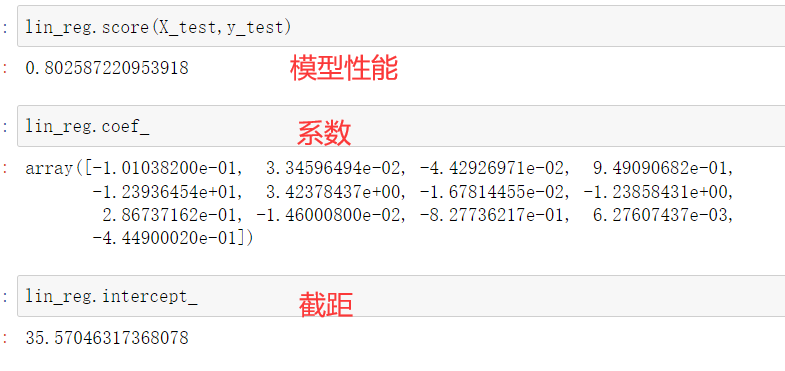
注意观察上图,上图中第一个特征值为负数,说明该特征与房价为负相关,即该特增大时,房价降低,反之,特征值的系数为正,则为正相关。
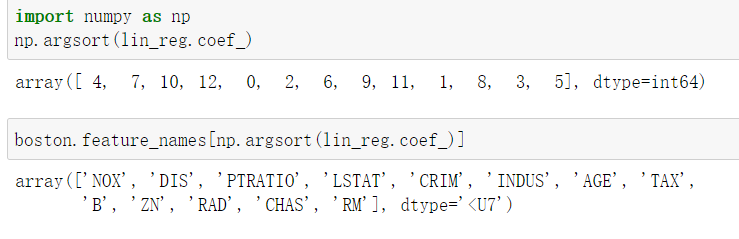
- 为了更好的看出哪个特征值的影响最大,哪个影响最小,我们需要对其进行排序,然后打印出来。如下图所示,从结果可看出,特征值RM(房间数量)对房价的影响最大。
import numpy as np
np.argsort(lin_reg.coef_)
boston.feature_names[np.argsort(lin_reg.coef_)]