分类:最长对称子串、动态规划
知识点:
-
生成二维数组 dp = [[0] * n for _ in range(n)]
-
求最大值 max(value1, value2)
-
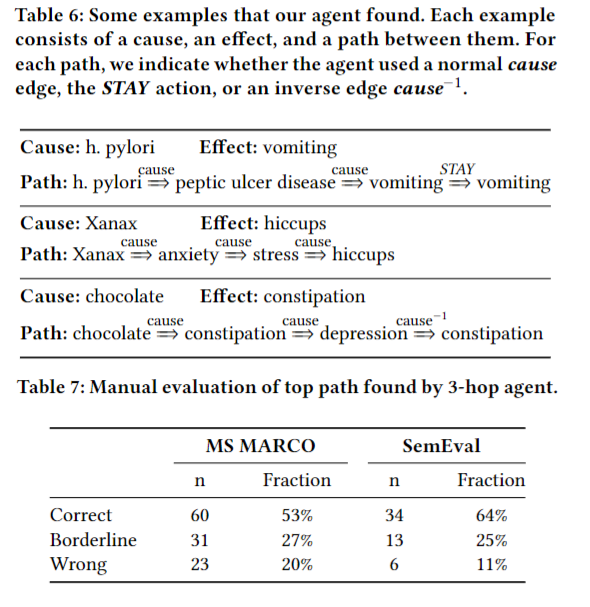
动态规划的步骤
a. 定义问题
长度为n下最长的对称子串的长度
b. 确定状态
dp[i][j]表示字符串从索引i到j的子串是否为对称子串。
c. 初始化状态
dp[j][j] = 1
d. 确定状态转移方程
dp[i][j]和dp[i-1][j-1]、dp[i-1][j]、dp[i][j-1]等的某种转换关系
题目来自【牛客】

找出最长对称子串
def findLongestSymmetricSubstring(s):
n = len(s)
# 用于存储状态的二维数组,
# dp[i][j]表示字符串从索引i到j的子串是否为有效的对称密码串
dp = [[0] * n for _ in range(n)]
max_length = 0 # 记录最大长度
# 遍历每个字符
for j in range(n):
dp[j][j] = 1 # 单个字符是对称的
# 从最近j的出发,所以i是从j-1到0
for i in range(j - 1, -1, -1):
# 如果首尾字符相同,且去除首尾字符后的子串是对称的 或者 是相邻字符
if s[i] == s[j] and (dp[i + 1][j - 1] or j - i <= 2):
dp[i][j] = 1
max_length = max(max_length, j - i + 1) # 更新最大长度
return max_length
# 输入
input_str = input()
# 获取最长有效密码串的长度并输出结果
result = findLongestSymmetricSubstring(input_str)
print(result)
findLongestSymmetricSubstring 函数使用动态规划来找到字符串中的最长有效对称密码串。基本思路是初始化一个二维数组 dp 用于记录状态,然后遍历字符串,更新数组中每个位置的状态,最终找到最长的有效密码串的长度并返回。