NO.1

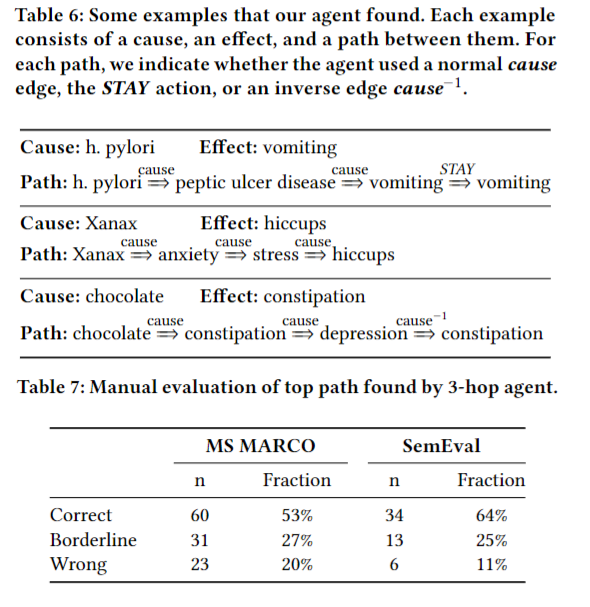
思路:递归。
代码实现:
class Solution {
public:
bool IsBalanced_Solution(TreeNode* pRoot) {
return dfs(pRoot)!=-1;
}
int dfs(TreeNode* root)
{
if(root==nullptr) return 0;
int left=dfs(root->left);
if(left==-1) return -1;
int right=dfs(root->right);
if(right==-1) return -1;
return abs(left-right)<=1?max(left,right)+1:-1;
}
};
NO.2

算法思路:
⼆维前缀和矩阵的应⽤。
a. 初始化⼆维前缀和矩阵;
b. 枚举所有的⼦矩阵,求出最⼤⼦矩阵。
代码实现:
#include <iostream>
using namespace std;
const int N = 110;
int n;
int dp[N][N];
int main()
{
int x;
cin >> n;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
cin >> x;
dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + x;
}
}
int ret = -127 * N;
for (int x1 = 1; x1 <= n; x1++)
{
for (int y1 = 1; y1 <= n; y1++)
{
for (int x2 = x1; x2 <= n; x2++)
{
for (int y2 = y1; y2 <= n; y2++)
{
ret = max(ret, dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 -
1] + dp[x1 - 1][y1 - 1]);
}
}
}
}
cout << ret << endl;
return 0;
}
NO.3
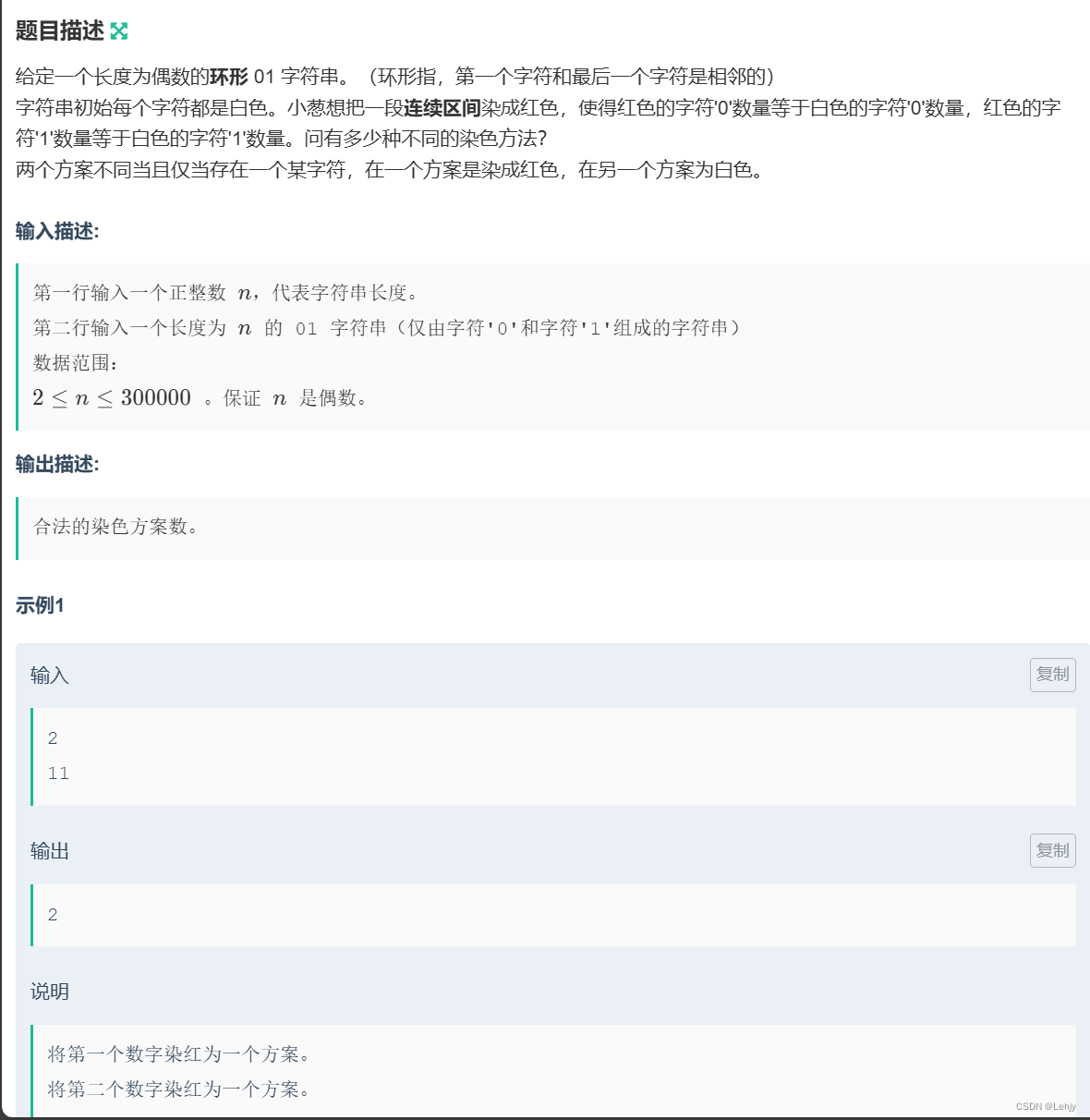
思路:滑动窗口,分别统计字符串中和窗口内0和1的数量,当窗口内字符串的数量为原字符串的一半,且该窗口内0和1的数量是外面字符串中0和1数量的一半时,就有两种方法。
代码实现:
#include <iostream>
#include <string>
using namespace std;
int n;
string s;
int main()
{
cin >> n >> s;
int sum[2] = { 0 }; // 统计字符串中所有 0 和 1 的个数
for (auto ch : s)
{
sum[ch - '0']++;
}
int left = 0, right = 0, ret = 0, half = n / 2;
int count[2] = { 0 }; // 统计窗⼝内 0 和 1 的个数
while (right < n - 1) // 细节问题
{
count[s[right] - '0']++;
while (right - left + 1 > half)
{
count[s[left++] - '0']--;
}
if (right - left + 1 == half)
{
if (count[0] * 2 == sum[0] && count[1] * 2 == sum[1])
{
ret += 2;
}
}
right++;
}
cout << ret << endl;
return 0;
}