提前预告,市赛初中组会考算法题,应该会有两道模板题
比如DFS BFS 二分 简单动态规划,虽然我们没学多久,但是模板题你还是要会写的
A题 编辑距离 动态规划
注意多组输入
#include<iostream>
using namespace std;
int dp[1005][1005];
//dp[i][j]把s字符串的前i个经过一系列操作变成b字符串的前j个的最小代价
char s[1005];
char b[1005];
int main(){
int n,m;
while(scanf("%d%s%d%s",&n,s+1,&m,b+1)!=EOF){
for(int i=0;i<=m;i++){
dp[0][i]=i; //插入
}
for(int i=0;i<=n;i++){
dp[i][0]=i; //删除
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(s[i]==b[j])dp[i][j]=dp[i-1][j-1];//此时i j位置相同,可以直接从s[i-1]->b[j-1] 转移过来
else{
dp[i][j]=min(dp[i-1][j-1]+1,min(dp[i-1][j]+1,dp[i][j-1]+1));
/*
dp[i-1][j]+1 表示我们把s[1~i] 删掉i位置,得到s[1~i-1] 从它变到b[1~j]
dp[i][j-1]+1 表示我们把s[1~i] 从它变到b[1~j-1] 然后插入一个b[j]
dp[i-1][j-1]+1 从s[1~i-1] 从它变到b[1~j-1] 对于s[i] 直接修改为b[j]
*/
}
}
}
printf("%d\n",dp[n][m]);
}
return 0;
}
B题 最长上升子序列 (N^2)版本
#include<iostream>
using namespace std;
int A[1005];
int dp[1005]; //dp[i]表示以A[i]结尾的最长上升子序列元素
int main(){
int n;
scanf("%d",&n);
int ans=1;
for(int i=1;i<=n;i++){
dp[i]=1;
scanf("%d",&A[i]);
for(int j=i-1;j>=1;j--){
if(A[j]<A[i]){
dp[i]=max(dp[i],dp[j]+1);
}
}//考虑拼接的方法,想寻得dp[i],往前面找,跟某个元素拼接起来 形成以A[i]
//结尾的上升子序列,那么所有的子序列取max也就是最大的
ans=max(ans,dp[i]);//但是答案不一定是以A[n]结尾
}
printf("%d",ans);
return 0;
}
当然,其实还有优化写法,利用二分,即可实现NlogN 的时间复杂度
我建议还是背一下(理解一下)
代码不是完全的,请看看思路
ll dp[N];
ll a[N];
ll b[N];
signed main() {
ll n;
read(n);
for(int i=1; i<=n; i++) {
read(a[i]);
}
ll cnt=0;
for(int i=1; i<=n; i++) {
if(cnt==0||a[i]>dp[cnt]) {
dp[++cnt]=a[i];//首位置要放入元素
//如果当前元素A【i】比当前序列结尾的还要大,放进来 上升
continue;
} else {
//如果当前元素A[i]≤ 序列结尾
//考虑查找序列里面合适的值,替换掉
//举例 1 100 2
//实际上用2替换100会更优,因为你过程的元素越大,越不利于后续上升
dp[upper_bound(dp+1,dp+1+cnt,a[i])-dp]=a[i];
}
}
printf("%lld",cnt);
}
右边的数字即全球通过人数

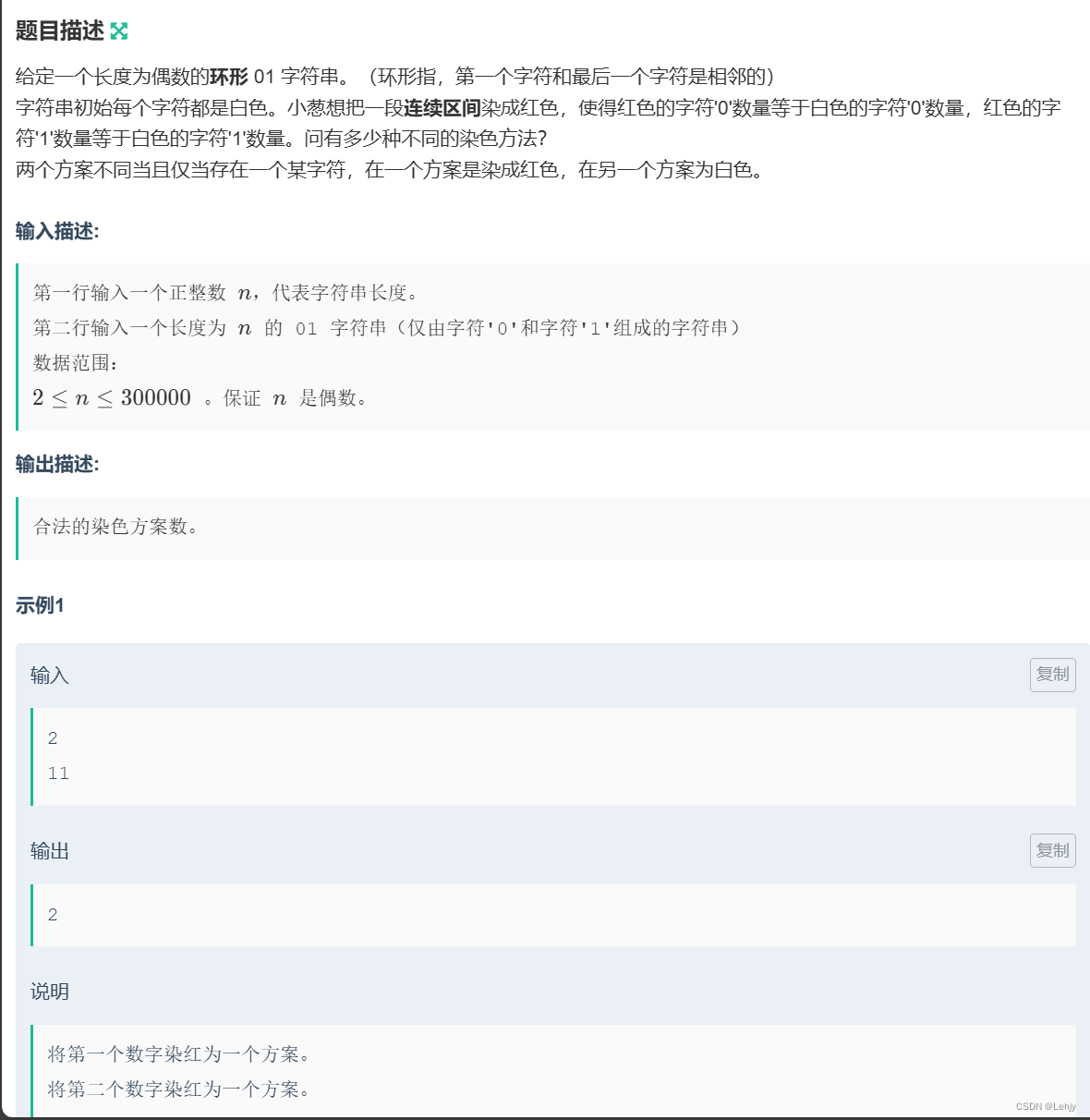
C题题解
我觉得这是不能错的题。
1
∗
1
1*1
1∗1的格子不用说了,啥地方都能放
主要看
2
∗
2
2*2
2∗2的,一个板只能放最多两个
2
∗
2
2*2
2∗2的
所以你要先计算出放
b
b
b个
2
∗
2
2*2
2∗2的要多少板 ,以及这些板还有多少个格子没放的。
如果多余没放的格子足够放完
a
a
a个
1
∗
1
1*1
1∗1的 ,那么答案就是
2
∗
2
2*2
2∗2需要的板子数
否则你还需要用(a-多余格子) 这么多个格子去计算还需要多少块板
#include<bits/stdc++.h>
using namespace std;
int main(){
int t;
scanf("%d",&t);
while(t--){
int a,b;
scanf("%d%d",&a,&b);
int le=0;
if(b%2==0)le=(15-8)*(b/2);
if(b%2){
le=(15-8)*(b/2)+15-4;
}
int ans=b/2+b%2;
if(a<=le)printf("%d\n",ans);
else{
printf("%d\n",ans+(a-le)/15+((a-le)%15!=0));
}
}
return 0;
}
D题题解
这其实就是个简单的模拟题,你把输入的字符串字母sort一遍,把密码表处理出来
然后枚举字符串开始翻译就行了
#include<bits/stdc++.h>
using namespace std;
char s[200005];
char b[30];
bool vis[30];
char sw[30];
int main(){
int t;
scanf("%d",&t);
while(t--){
memset(vis,false,sizeof(vis));
int n;
scanf("%d",&n);
scanf("%s",s+1);
int len=0;
for(int i=1;i<=n;i++){
if(vis[s[i]-'a'])continue;
else{
vis[s[i]-'a']=true;
b[++len]=s[i];
}
}
sort(b+1,b+1+len);
for(int i=1;i<=len/2+1;i++){
sw[b[i]-'a']=b[len-i+1];
sw[b[len-i+1]-'a']=b[i];
}
for(int i=1;i<=n;i++){
s[i]=sw[s[i]-'a'];
}
printf("%s\n",s+1);
}
return 0;
}
E题题解
这个标记题需要一定数理知识
对于一个三元组
A
[
i
−
2
]
,
A
[
i
−
1
]
,
A
[
i
]
{A[i-2],A[i-1],A[i]}
A[i−2],A[i−1],A[i] 我们得标记它们,你可以想象一下,什么样的三元组能相互之间算答案?有两个元素一样对不对,我们直接把一样的元素标记起来,记为一个二元组。
以此标记该三元组里面的二元组,按顺序标记
每次计算答案的时候,查找一下当前三元组前面,有多少个跟自己的二元组一样的三元组,该操作不保证过滤了重复元素
因此我们需要查询该三元组前面有多少个跟自己一模一样的三元组,因为一模一样是不会产生答案的,所以要减去3倍
#include<bits/stdc++.h>
using namespace std;
int A[200005];
map<pair<int,int>,int >vis_1;
map<pair<int,int>,int >vis_2;
map<pair<int,int>,int >vis_3;
map<pair<pair<int,int>,int> ,int >pre;
int main(){
int t;
scanf("%d",&t);
while(t--){
int n;
scanf("%d",&n);
long long int ans=0;
for(int i=1;i<=n;i++){
scanf("%d",&A[i]);
if(i>=3){
// 当前三元组A[i-2] A[i-1] A[i]
// 三种可能: A[i-2]A[i]相等 A[i-1]A[i]相等 A[i-2]A[i-1]相等 这三个二元组可以作为标记去查询
ans=ans+vis_1[make_pair(A[i-2],A[i-1])];
//统计前面有多少个跟A[i-2] A[i-1]值一样的二元组(先不考虑前面存在跟自己完全一样的三元组,那么答案就是加这个二元组标记的个数,视作前面出现的该二元组的元素与当前A[i]都不一样)
//A[i-2] A[i-1] ? 前面的一些三元组结构
//A[i-2] A[i-1] A[i] 当前三元组
ans=ans+vis_2[make_pair(A[i-2],A[i])];
ans=ans+vis_3[make_pair(A[i-1],A[i])];
vis_1[make_pair(A[i-2],A[i-1])]++;
vis_2[make_pair(A[i-2],A[i])]++;
vis_3[make_pair(A[i-1],A[i])]++;
ans=ans-3*pre[make_pair(make_pair(A[i-2],A[i-1]),A[i])];
//考虑存在重复的问题,举例
//如果前面有x个三元组满足值与当前三元组(A[i-2],A[i-1],A[i])一样,那么我们就多计算了x个答案,因为完全相等的三元组不产生答案贡献,枚举了三个二元组,所以减法要减去*3
pre[make_pair(make_pair(A[i-2],A[i-1]),A[i])]++;
}
}
printf("%lld\n",ans);
vis_1.clear();
vis_2.clear();
vis_3.clear();
pre.clear();
}
return 0;
}
F题题解
考虑东西南北指令,划分为两部分
一个部分是: 北南凑一对,相当于抵消移动 东西凑一对,相当于抵消移动
第一部分完成后,未凑对的剩下来的只能是北/南里面的一种,剩下的我们要考虑能不能均分给两个人,同理东西
计算北南的对数,东西的对数
北南可以按A人先的顺序轮流分配
东西可以按B人先的顺序轮流分配
接下来分配剩余的未配对的,注意如果剩余奇数个,肯定不能保证最终两个人走在同一个地方
#include<bits/stdc++.h>
using namespace std;
char s[200005];
int vis[30];
int A[30];
int B[30];
int main(){
int t;
scanf("%d",&t);
int N,S,E,W;
N='N'-'A';
S='S'-'A';
E='E'-'A';
W='W'-'A';
while(t--){
int n;
scanf("%d",&n);
scanf("%s",s+1);
vis[N]=vis[S]=vis[E]=vis[W]=0;
A[N]=A[S]=A[E]=A[W]=0;
B[N]=B[S]=B[E]=B[W]=0;
for(int i=1;i<=n;i++){
vis[s[i]-'A']++;
}
int ns=min(vis[N],vis[S]);
int ew=min(vis[E],vis[W]);//配对相消
int lens=max(vis[N],vis[S])-min(vis[N],vis[S]);
int leew=max(vis[E],vis[W])-min(vis[E],vis[W]);
for(int i=1;i<=ns;i++){
if(i%2){
A[N]++;
A[S]++;
}
else{
B[N]++;
B[S]++;
}
}
for(int i=1;i<=ew;i++){
if(i%2){
B[E]++;
B[W]++;
}
else{
A[E]++;
A[W]++;
}
}
//双消+偶数
//单消 + 偶
if(lens%2||leew%2){
printf("NO\n");
}
else{
int op;
if(vis[N]>vis[S])op=N;
else op=S;
A[op]+=lens/2;
B[op]+=lens/2;
if(vis[E]>vis[W])op=E;
else op=W;
A[op]+=leew/2;
B[op]+=leew/2;
if((A[N]+A[S]+A[E]+A[W])==0||(B[N]+B[S]+B[E]+B[W])==0){
printf("NO\n");continue;
}
for(int i=1;i<=n;i++){
if(A[s[i]-'A']){
A[s[i]-'A']--;
printf("R");
}
else{
B[s[i]-'A']--;
printf("H");
}
}
printf("\n");
}
}
return 0;
}