课程地址：《菜菜的机器学习sklearn课堂》_哔哩哔哩_bilibili

• 第一期：sklearn入门 & 决策树在sklearn中的实现
• 第二期：随机森林在sklearn中的实现
• 第三期：sklearn中的数据预处理和特征工程
• 第四期：sklearn中的降维算法PCA和SVD
• 第五期：sklearn中的逻辑回归
• 第六期：sklearn中的聚类算法K-Means
• 第七期：sklearn中的支持向量机SVM（上）
• 第八期：sklearn中的支持向量机SVM（下）
• 第九期：sklearn中的线性回归大家族
• 第十期：sklearn中的朴素贝叶斯
• 第十一期：sklearn与XGBoost
• 第十二期：sklearn中的神经网络

---

目录

案例一：用PCA做噪音过滤（inverse_transform）

（1）导入数据并探索

（2）定义画图函数

（3）为数据加上噪音

（4）降维

（5）逆转降维结果，实现降噪

PCA类的重要接口、参数和属性总结 

重要参数

重要属性

重要接口

案例二：PCA对手写数字数据集的降维

（1）导入数据并探索

（2）画累计方差贡献率曲线，找最佳降维后维度的范围

（3）降维后维度的学习曲线，继续缩小最佳维度的范围

（4）细化学习曲线，找出降维后的最佳维度

（5）导入找出的最佳维度进行降维，查看模型效果

（6）现在特征数量已经不足之前的3%，换模型如何

（7）KNN的k值学习曲线

（8）定下超参数后，模型效果和运行时间如何

---

案例一：用PCA做噪音过滤（inverse_transform）

降维的目的之一就是希望抛弃掉对模型带来负面影响的特征（带有效信息的特征的方差应是远大于噪音的），所以相比噪音，有效的特征所带的信息应该不会在PCA过程中被大量抛弃

inverse_transform能够在不恢复原始数据的情况下，将降维后的数据返回到原本的高维空间，即能够实现 “保证维度，但去掉方差很小特征所带的信息” 。利用该性质能够实现噪音过滤

（1）导入数据并探索

from sklearn.datasets import load_digits   # 手写数字（本质是图像）
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import numpy as np

digits = load_digits()
digits.data.shape  #(1797, 64)
digits.images.shape  #(1797, 8, 8)  1797个数字，每个数字是8行8列的特征矩阵

set(digits.target.tolist())  #查看target有哪几个数  {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
# digits.target是array
# .tolist()转成列表
# set()去重查看

（2）定义画图函数

# 定义画图函数
def plot_digits(data):
    #data的结构必须是（m,n），并且n=64要能够被分成（8,8）这样的结构
    fig, axes = plt.subplots(4,10  # 4行0-9
                             ,figsize=(10,4)
                             ,subplot_kw = {"xticks":[],"yticks":[]}
                            )
    for i, ax in enumerate(axes.flat):
        ax.imshow(data[i].reshape(8,8),cmap="binary")
        
plot_digits(digits.data)

（3）为数据加上噪音

# 为数据加上噪音
rng = np.random.RandomState(42)  # 规定numpy中的随机模式
 
#在指定的数据集中，随机抽取服从正态分布的数据
#两个参数，分别是指定的数据集，和抽取出来的正态分布的方差
#方差越大，随机抽取出的数字就会越凌乱
noisy = rng.normal(digits.data,2)   #np.random.normal(digits.data,2)
noisy.shape   # (1797,64)
 
plot_digits(noisy)

（4）降维

# 降维
pca = PCA(0.5,svd_solver='full').fit(noisy)  # 原数据信息能保留50%的特征
X_dr = pca.transform(noisy)
X_dr.shape  #(1797, 6)   # 把维度从64降到了6，认为含有噪音的大部分特征都被删掉了，前6个特征应该包含了原始数据的大部分有效特征
# 无法可视化X_dr，因为画图函数要求输入的data第二维是64（能够被分成(8,8)）

（5）逆转降维结果，实现降噪

# 逆转降维结果，实现降噪
without_noise = pca.inverse_transform(X_dr)   # (1797,64)
plot_digits(without_noise)

---

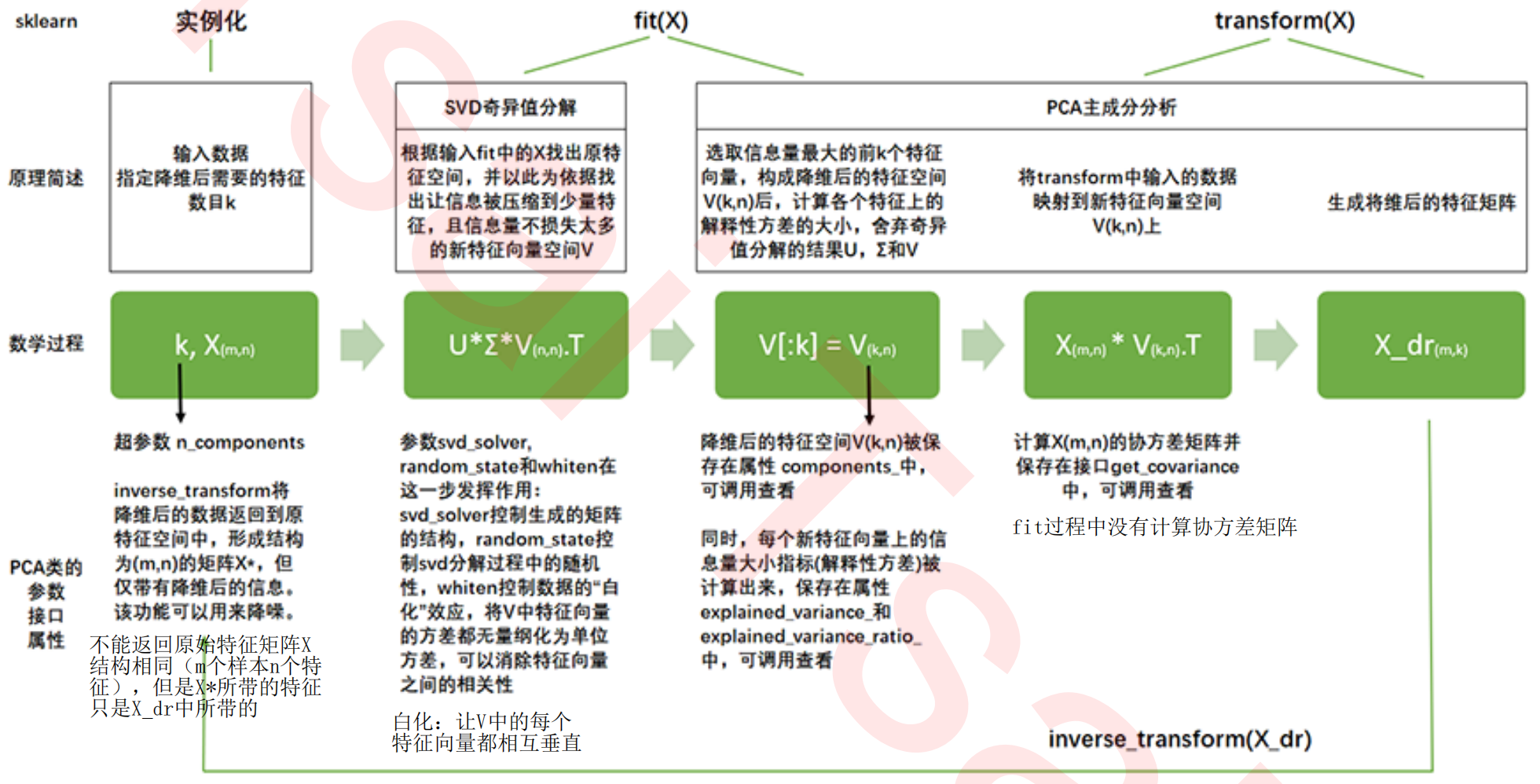
PCA类的重要接口、参数和属性总结 

重要参数

• n_components：降维后需要的特征数目k；鸢尾花高维数据可视化
• svd_solver：控制生成的矩阵的结构；为什么PCA中有SVD相关的参数；sklearn中PCA和SVD联合降维的流程
• random_state：控制SVD的参数中一些拥有随机矩阵分解模式的参数

重要属性

• components_：调用新特征空间降维后的矩阵V(k,n)
• explained_variance_：可解释性方差，衡量降维后每个特征所带的信息量
• explained_variance_ratio_：可解释性方差贡献率，画图，选择最佳的n_components

重要接口

• fit：拟合数据
• transform：调取结果
• fit_transform：拟合+调取结果一步完成
• inverse_transform：人脸识别中的逆转；手写数字的噪音过滤

---

案例二：PCA对手写数字数据集的降维

回顾：特征工程章节中使用的手写数字数据集，结构为(42000,784) 

• KNN准确率 0.966 > 随机森林 0.937，但KNN花费时间太长
• 使用嵌入法 SelectFromModel 对数据集进行特征选择，选出324个特征，将随机森林的效果也调的接近于KNN了（0.964）
• 试着用PCA处理该数据

【3 - 特征工程】菜菜sklearn机器学习_如何原谅奋力过但无声的博客-CSDN博客

（1）导入数据并探索

from sklearn.decomposition import PCA
from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.model_selection import cross_val_score
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np

data = pd.read_csv(r"D:\Jupyter Notebook\菜菜sklearn\3 数据预处理和特征工程\digit recognizor.csv")
 
X = data.iloc[:,1:]
y = data.iloc[:,0]

X.shape  #(42000, 784)

降维之前要确定超参数n_components，若PCA()不填，则默认返回min(X.shape) 

（2）画累计方差贡献率曲线，找最佳降维后维度的范围

pca_line = PCA().fit(X)  # 默认是min(X.shape)=784
plt.figure(figsize=[20,5])   # 图像的尺寸
plt.plot(np.cumsum(pca_line.explained_variance_ratio_))   # 返回784个特征的方差贡献率
plt.xlabel("number of components after dimension reduction")  # 降维后的特征数目
plt.ylabel("cumulative explained variance ratio")  # 累计可解释性方差比率和
plt.show()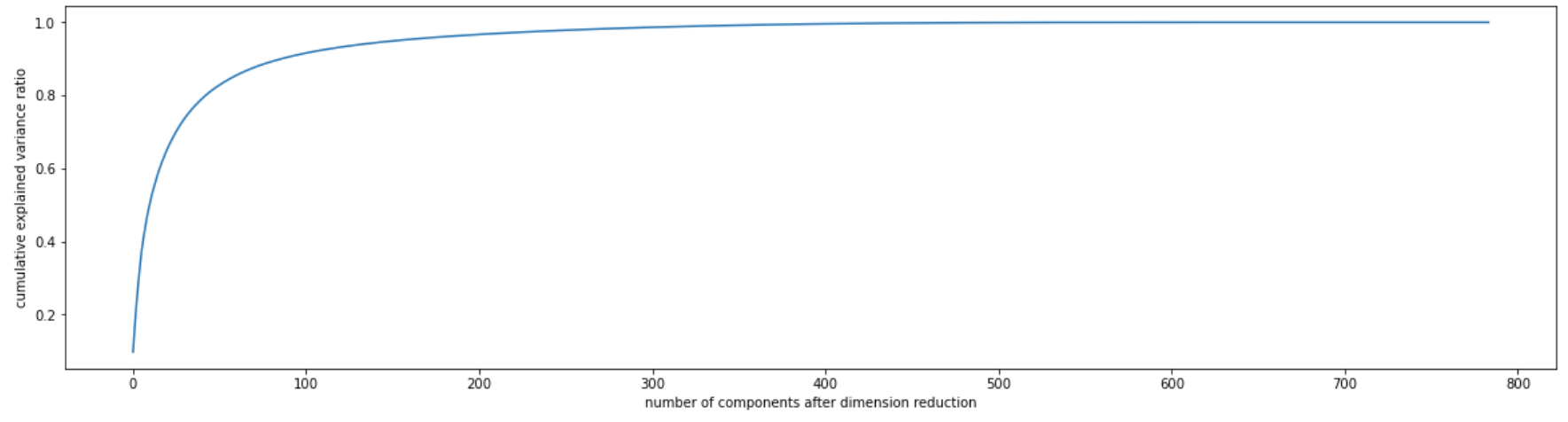

选转折点作为n_components，由图可以看到，1-100中必有一个值是想要的 

（3）降维后维度的学习曲线，继续缩小最佳维度的范围

PCA的参数 n_components 取不同值时，随机森林在交叉验证下的效果（使用降维后的特征矩阵）

score = []
for i in range(1,101,10):
    X_dr = PCA(i).fit_transform(X)  # 降维后的结果X_dr
    once = cross_val_score(RFC(n_estimators=10,random_state=0)  # 实例化的模型
                           ,X_dr,y,cv=5).mean()
    score.append(once)
plt.figure(figsize=[20,5])
plt.plot(range(1,101,10),score)  # x轴和y轴的取值
plt.show()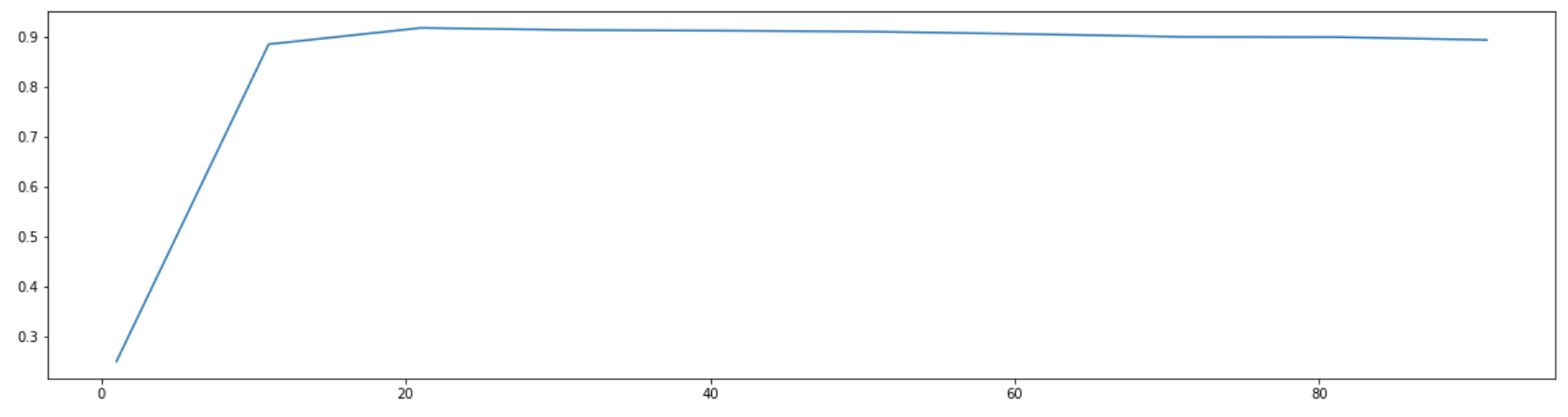

可以看出，大概降到20维左右模型的效果最好，后面曲线几乎平了 

（4）细化学习曲线，找出降维后的最佳维度

score = []
for i in range(10,25):
    X_dr = PCA(i).fit_transform(X)
    once = cross_val_score(RFC(n_estimators=10,random_state=0),X_dr,y,cv=5).mean()
    score.append(once)
plt.figure(figsize=[20,5])
plt.plot(range(10,25),score)
plt.show()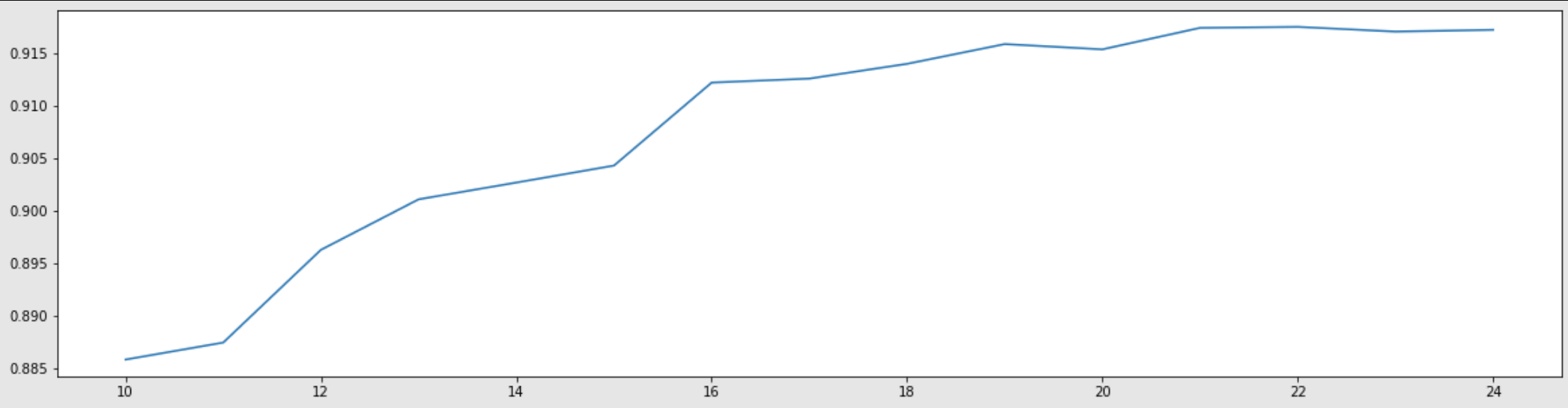

差不多21左右是最大值 

（5）导入找出的最佳维度进行降维，查看模型效果

X_dr = PCA(21).fit_transform(X)
cross_val_score(RFC(n_estimators=10,random_state=0),X_dr,y,cv=5).mean()  #0.9174523809523809

# n_estimators越大，泛化误差越小，模型精度上升
cross_val_score(RFC(n_estimators=100,random_state=0),X_dr,y,cv=5).mean() #0.9443333333333334

模型效果还好（0.944），但还是没有使用嵌入法特征选择后的 0.964 高。如何再提高模型表现？

（6）现在特征数量已经不足原来的3%，换模型如何？

在之前的建模过程中，因为计算量太大，所以一直使用随机森林，但事实上KNN效果比随机森林更好。KNN在未调参的状况下已经达到96.6%的准确率，而随机森林在未调参前只能达到93.7%，这是模型本身的限制带来的

现在特征数量已经降到不足原来的3%，换KNN看看效果如何

from sklearn.neighbors import KNeighborsClassifier as KNN
cross_val_score(KNN(),X_dr,y,cv=5).mean()  #KNN()的值不填写默认=5   0.9679761904761905

（7）KNN的k值学习曲线

score = []
for i in range(10):
    X_dr = PCA(21).fit_transform(X)
    once = cross_val_score(KNN(i+1),X_dr,y,cv=5).mean()   # KNN()中的参数最小是1
    score.append(once)
plt.figure(figsize=[20,5])
plt.plot(range(10),score)
plt.show()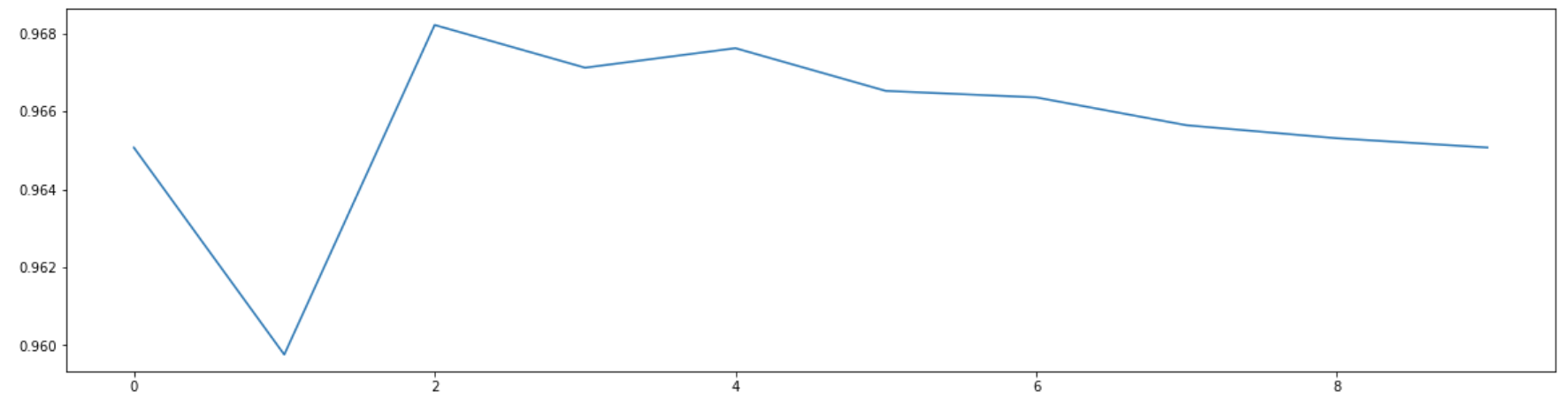

可以看到，横坐标取2时效果最好，此时KNN的参数是2+1=3 

（8）定下超参数后，模型效果和运行时间如何？

cross_val_score(KNN(3),X_dr,y,cv=5).mean()  #KNN()的值不填写默认=5

%%timeit
cross_val_score(KNN(3),X_dr,y,cv=5).mean()

原本784列的特征被缩减到21列之后，用KNN跑出了目前为止这个数据集上最好的结果0.968