文章目录
- 一、线性回归手动实现与模型局限
- 1. 线性回归的手动实现
- 2. 线性回归模型局限
- 3. 线性回归的决定系数
- 二、机器学习模型结果可信度理论与交叉验证基础
- 1. 机器学习模型结果可信度理论基础与数据集划分
- 1.1 机器学习模型结果可信度基础理论
- 1.2 数据集切分方法
- 1.3 线性回归手动实现
- 1.4 测试集的不可知悖论
- 2. 交叉验证基本思想
一、线性回归手动实现与模型局限
- 在创建好了数据生成器之后,接下来即可进行手动线性回归建模实验。
# 科学计算模块
import numpy as np
import pandas as pd
# 绘图模块
import matplotlib as mpl
import matplotlib.pyplot as plt
# 自定义模块
from ML_basic_function import *
1. 线性回归的手动实现
- 接下来,我们尝试进行线性回归模型的手动建模实验。建模过程将遵照机器学习的一般建模流程,并且借助 NumPy 所提供的相关工具来进行实现。
- 根据机器学习建模流程构建线性回归模型,可分为以下几步。
- (1) 数据准备。
- 我们利用数据生成器创建一个扰动项不太大的数据集:
# 设置随机数种子
np.random.seed(24)
# 扰动项取值为0.01
features, labels = arrayGenReg(delta=0.01)
features
#array([[ 1.76405235, 0.40015721, 1. ],
# [ 0.97873798, 2.2408932 , 1. ],
# [ 1.86755799, -0.97727788, 1. ],
# ...,
# [ 0.19782817, 0.0977508 , 1. ],
# [ 1.40152342, 0.15843385, 1. ],
# [-1.14190142, -1.31097037, 1. ]])
labels
- labels 得到如下数据。

- (2) 模型选取。
- 选取模型对上述回归类问题数据进行建模。此处我们选取带有截距项的多元线性回归方程进行建模,基本模型为: f ( x ) = w 1 x 1 + w 2 x 2 + b f(x) = w_1x_1+w_2x_2+b f(x)=w1x1+w2x2+b
- 令
w
^
=
[
w
1
,
w
2
,
b
]
T
\hat w = [w_1,w_2,b]^T
w^=[w1,w2,b]T,
x
^
=
[
x
1
,
x
2
,
1
]
T
\hat x = [x_1,x_2, 1]^T
x^=[x1,x2,1]T,则上式可写为
f ( x ) = w ^ T x ^ f(x) = \hat w^T\hat x f(x)=w^Tx^ - 此处如果要构建一个不带截距项的模型,则可令 X 为原始特征矩阵带入进行建模。
- (3) 构造损失函数。
- 对于线性回归来说,我们可以参照 SSE、MSE 或者 RMSE 的计算过程构造损失函数。
- 由于目前模型参数还只是隐式的值(在代码中并不显示),我们可以简单尝试,通过人工设置一组 w ^ \hat w w^ 来计算 SSE。
- 令 w ^ \hat w w^ 为一组随机值,计算 SSE。
np.random.seed(24)
w = np.random.randn(3).reshape(-1, 1)
w
#array([[ 1.32921217],
# [-0.77003345],
# [-0.31628036]])
- 此时模型输出结果为:
y_hat = features.dot(w)
y_hat[:10]
#array([[ 2.04347616],
# [ 0.02627308],
# [-0.63176501],
# [ 0.20623364],
# [-2.64718921],
# [-0.86880796],
# [ 0.88171608],
# [-1.61055557],
# [ 0.80113619],
# [-0.49279524]])
- 据此,根据公式 S S E = ∣ ∣ y − X w ^ ∣ ∣ 2 2 = ( y − y ^ ) T ( y − y ^ ) SSE= ||y - X\hat w||_2^2 = (y - \hat y)^T(y - \hat y) SSE=∣∣y−Xw^∣∣22=(y−y^)T(y−y^),SSE 计算结果为:
(labels - y_hat).T.dot(labels - y_hat)
#array([[2093.52940481]])
# 计算MSE
(labels - y_hat).T.dot(labels - y_hat) / len(labels)
#array([[2.0935294]])
labels[:10]
#array([[ 4.43811826],
# [ 1.375912 ],
# [ 0.30286597],
# [ 1.81970897],
# [-2.47783626],
# [ 0.47374318],
# [ 2.83085905],
# [-0.83695165],
# [ 2.84344069],
# [ 0.8176895 ]])
- 能够看出,在当前参数取值下,模型输出结果和真实结果相距甚远。
- 不过,为了后续快速计算 SSE,我们可以将上述 SSE 计算过程封装为一个函数,令其在输入特征矩阵、标签数组和真实参数情况下即可输出 SSE 计算结果:
def SSELoss(X, w, y):
"""
SSE计算函数
:param X:输入数据的特征矩阵
:param w:线性方程参数
:param y:输入数据的标签数组
:return SSE:返回对应数据集预测结果和真实结果的误差平方和
"""
y_hat = X.dot(w)
SSE = (y - y_hat).T.dot(y - y_hat)
return SSE
# 简单测试函数性能
SSELoss(features, w, labels)
#array([[2093.52940481]])
- 实验结束后,需要将上述 SSELoss 函数写入 ML_basic_function.py 中。
- (4) 利用最小二乘法求解损失函数。
- 我们需要在 SSELoss 中找到一组最佳的参数取值,另模型预测结果和真实结果尽可能接近。此处我们利用最小二乘法来进行求解,最小二乘法求解模型参数公式为: w ^ = ( X T X ) − 1 X T y \hat w = (X^TX)^{-1}X^Ty w^=(XTX)−1XTy
- 值得注意的是,最小二乘法在进行求解过程中,需要特征矩阵的交叉乘积可逆,也就是 X T X X^TX XTX 必须存在逆矩阵。我们可以通过计算其行列式来判断该条件是否满足:
np.linalg.det(features.T.dot(features))
#967456500.1798325
- 行列式不为 0,因此 X T X X^TX XTX 逆矩阵存在,可以通过最小二乘法求解。具体求解方法分为两种,其一是使用 NumPy 中线性代数基本方法,根据上述公式进行求解,其二是直接使用 lstsq 函数进行求解。
- 基础方法求解
w = np.linalg.inv(features.T.dot(features)).dot(features.T).dot(labels)
w
#array([[ 1.99961892],
# [-0.99985281],
# [ 0.99970541]])
- 即可算出模型最优参数 w。所谓模型最优参数,指的是参数取得任何其他数值,模型评估结果都不如该组参数时计算结果更好。首先,我们也可以计算此时模型 SSE 指标:
SSELoss(features, w, labels)
array([[0.09300731]])
- 明显小于此前所采用的随机 w 取值时 SSE 结果。此外,我们还可以计算模型 MSE
SSELoss(features, w, labels) / len(y)
array([[9.30073138e-05]])
- 模型评估指标中 SSE、MSE、RMSE 三者反应的是一个事实,我们根据 SSE 构建损失函数只是因为 SSE 计算函数能够非常方便的进行最小值推导,SSE 取得最小值时 MSE、RMSE 也取得最小值。
- lstsq 函数求解
- 当然,我们也可以利用 lstsq 函数进行最小二乘法结果求解。二者结果一致。
np.linalg.lstsq(features, labels, rcond=-1)
#(array([[ 1.99961892],
# [-0.99985281],
# [ 0.99970541]]),
# array([0.09300731]),
# 3,
# array([32.70582436, 31.3166949 , 30.3678959 ]))
- 最终 w 参数取值为:
np.linalg.lstsq(features, labels, rcond=-1)[0]
#array([[ 1.99961892],
# [-0.99985281],
# [ 0.99970541]])
2. 线性回归模型局限
- 尽管上述建模过程能够发现,面对白噪声不是很大、并且线性相关性非常明显的数据集,模型整体表现较好,但在实际应用中,大多数数据集可能都不具备明显的线性相关性,并且存在一定的白噪声(数据误差)。此时多元线性回归模型效果会受到极大影响。
plt.plot(features[:, 0], labels, 'o')
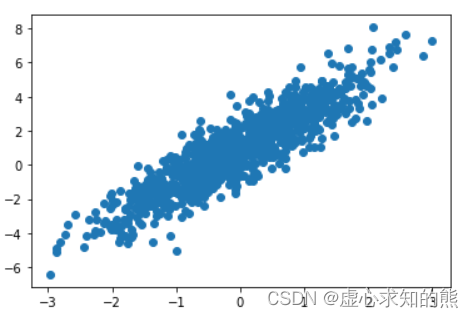
- 非线性相关规律
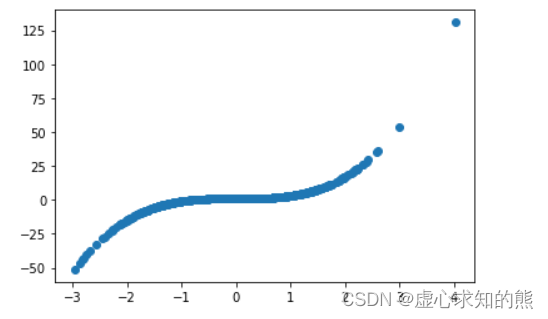
- 例如,此处创建一个满足 y = x 3 + 1 y=x^3+1 y=x3+1 基本规律,并且白噪声很小的数据集进行建模测试。
# 设置随机数种子
np.random.seed(24)
# 扰动项取值为0.01
features, labels = arrayGenReg(w=[2,1], deg=3, delta=0.01)
features
#array([[ 1.32921217, 1. ],
# [-0.77003345, 1. ],
# [-0.31628036, 1. ],
# ...,
# [ 0.84682091, 1. ],
# [ 1.73889649, 1. ],
# [ 1.93991673, 1. ]])
plt.plot(features[:, 0], labels, 'o')
- 进行最小二乘法模型参数求解。
np.linalg.lstsq(features, labels, rcond=-1)
#(array([[5.91925985],
# [0.96963333]]),
# array([28466.58711077]),
# 2,
# array([32.13187164, 31.53261742]))
w = np.linalg.lstsq(features, labels, rcond=-1)[0]
w
#array([[5.91925985],
# [0.96963333]])
SSELoss(features, w, labels)
#array([[28466.58711077]])
y_hat = features.dot(w)
y_hat
plt.plot(features[:, 0], labels, 'o')
plt.plot(features[:, 0], y_hat, 'r-')
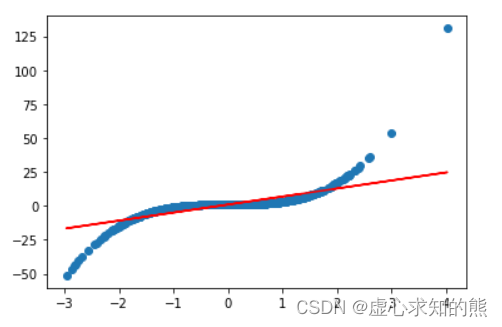
- 从模型结果能够看出,模型和数据集分布规律相差较大。
- 噪声增加。
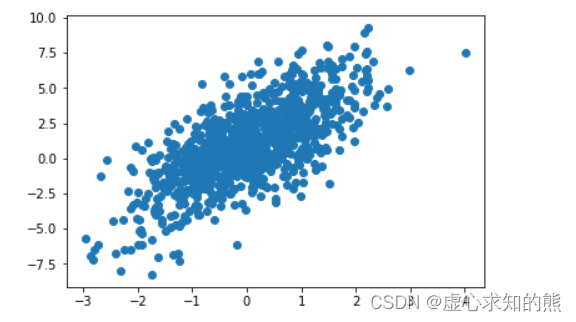
- 我们稍微增加模型白噪声,测试线性回归模型效果。
# 设置随机数种子
np.random.seed(24)
# 扰动项取值为2
features, labels = arrayGenReg(w=[2,1], delta=2)
features
#array([[ 1.32921217, 1. ],
# [-0.77003345, 1. ],
# [-0.31628036, 1. ],
# ...,
# [ 0.84682091, 1. ],
# [ 1.73889649, 1. ],
# [ 1.93991673, 1. ]])
plt.plot(features[:, 0], labels, 'o')
np.linalg.lstsq(features, labels, rcond=-1)
#(array([[1.91605821],
# [0.90602215]]),
# array([3767.12804359]),
# 2,
# array([32.13187164, 31.53261742]))
w = np.linalg.lstsq(features, labels, rcond=-1)[0]
w
#array([[1.91605821],
# [0.90602215]])
SSELoss(features, w, labels)
#array([[3767.12804359]])
X = np.linspace(-5, 5, 1000)
y = w[0] * X + w[1]
plt.plot(features[:, 0], labels, 'o')
plt.plot(X, y, 'r-')
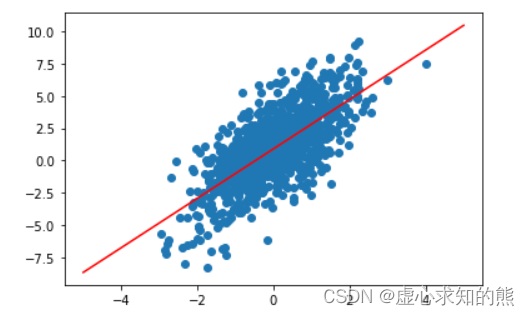
- 能够发现,模型误差较大。
- 最小二乘法条件限制
- 除此之外,线性回归模型还面临这一个重大问题就是,如果特征矩阵的交叉乘积不可逆,则最小二乘法求解过程就不成立了。 w ^ = ( X T X ) − 1 X T y \hat w = (X^TX)^{-1}X^Ty w^=(XTX)−1XTy
- 当然,此时也代表着数据集存在着较为严重的多重共线性,换而言之就是数据集的特征矩阵可能可以相互线性表出。这个时候矩阵方程 X T X w ^ = X T y X^TX\hat w=X^Ty XTXw^=XTy 并不一定存在唯一解。
- 解决该问题的方法有很多种,从数学角度出发,我们可以从以下三个方面入手:
- (1) 对数据进行降维处理
- 首先,可考虑进一步对数据集进行 SVD 分解或 PCA 主成分分析,在 SVD 或 PCA 执行的过程中会对数据集进行正交变换,最终所得数据集各列将不存在任何相关性。当然此举会对数据集的结构进行改变,且各列特征变得不可解释。
- (2) 修改求解损失函数的方法
- 我们可以试图求解原方程的广义逆矩阵,对于某些矩阵方程来说,通过求解广义逆矩阵,也可以得到近似最优解;此外,我们还可以通过使用其他最优化求解方法,如梯度下降算法等来进行求解。
- (3) 修改损失函数
- 修改原损失函数,令其满足最小二乘法求解条件即可。如果 X T X XTX XTX 不可逆,那么我们可以通过试图在损失函数中加入一个正则化项,从而令损失函数可解。根据SSE所构建的损失函数如下: S S E L o s s ( w ^ ) = ∣ ∣ y − X w ^ ∣ ∣ 2 2 = ( y − X w ^ ) T ( y − X w ^ ) SSELoss(\hat w) = ||y - X\hat w||_2^2 = (y - X\hat w)^T(y - X\hat w) SSELoss(w^)=∣∣y−Xw^∣∣22=(y−Xw^)T(y−Xw^)
- 通过数学过程可以证明,此时如果我们在原有损失函数基础上添加一个关于参数 w w w 的 1- 范数( ∣ ∣ w ^ ∣ ∣ 1 ||\hat w||_1 ∣∣w^∣∣1)或者 2- 范数( ∣ ∣ w ^ ∣ ∣ 2 ||\hat w||_2 ∣∣w^∣∣2)的某个计算结果,则可令最小二乘法条件得到满足。
- 此时最小二乘法计算结果由无偏估计变为有偏估计。例如,当我们在损失函数中加上 λ ∣ ∣ w ^ ∣ ∣ 2 2 \lambda ||\hat w||_2^2 λ∣∣w^∣∣22(其中 λ \lambda λ 为参数)时,模型损失函数为: L o s s ( w ^ ) = ∣ ∣ y − X w ^ ∣ ∣ 2 2 + λ ∣ ∣ w ^ ∣ ∣ 2 2 Loss(\hat w) = ||y - X\hat w||_2^2 +\lambda ||\hat w||_2^2 Loss(w^)=∣∣y−Xw^∣∣22+λ∣∣w^∣∣22
- 经过数学转化,上述矩阵表达式对 w ^ \hat w w^ 求导后令其为零,则可解出: ( X T X + λ I ) w ^ = X T y (X^TX+\lambda I) \hat w = X^Ty (XTX+λI)w^=XTy
- 其中 I I I 为单位矩阵。此时由于 ( X T X + λ I ) (X^TX+\lambda I) (XTX+λI) 肯定是可逆矩阵,因此可以顺利求解出 w ^ \hat w w^: w ^ = ( X T X + λ I ) − 1 X T y \hat w = (X^TX+\lambda I)^{-1}X^Ty w^=(XTX+λI)−1XTy
- 该过程也被称为岭回归。而类似的,如果是通过添加了 w ^ \hat w w^ 的 1- 范数的某个表达式,从而构造损失函数如下: L o s s ( w ^ ) = ∣ ∣ y − X w ^ ∣ ∣ 2 2 + λ ∣ ∣ w ^ ∣ ∣ 1 Loss(\hat w) = ||y - X\hat w||_2^2 +\lambda ||\hat w||_1 Loss(w^)=∣∣y−Xw^∣∣22+λ∣∣w^∣∣1
- 则该过程被称为 Lasso。而更进一步,如果构建的损失函数同时包含 w ^ \hat w w^ 的 1- 范数和 2- 范数,形如如下形式: L o s s ( w ^ ) = 1 2 n ∣ ∣ y − X w ^ ∣ ∣ 2 2 + λ α ∣ ∣ w ^ ∣ ∣ 1 + λ ( 1 − α ) 2 ∣ ∣ w ^ ∣ ∣ 2 2 Loss(\hat w) = \frac{1}{2n}||y - X\hat w||_2^2 + \lambda \alpha ||\hat w||_1 +\frac{\lambda(1-\alpha)}{2} ||\hat w||_2 ^ 2 Loss(w^)=2n1∣∣y−Xw^∣∣22+λα∣∣w^∣∣1+2λ(1−α)∣∣w^∣∣22
- 则构建的是弹性网模型(Elastic-Net),其中 λ 、 α \lambda、\alpha λ、α 都是参数,n 是样本个数。不难发现,岭回归和 Lasso 其实都是弹性网的一种特殊形式。
- 其中,1- 范数也被称为 L1 范数,将参数的 1- 范数添加入损失函数的做法,也被称为损失函数的 L1 正则化,L2 正则化也类似。在大多数情况下,添加正则化项也可称为添加惩罚函数 p ( w ) p(w) p(w),核心作用是缓解模型过拟合倾向。
3. 线性回归的决定系数
- 对于线性回归模型来说,除了 SSE 以外,我们还可使用决定系数(R-square,也被称为拟合优度检验)作为其模型评估指标。
- 决定系数的计算需要使用之前介绍的组间误差平方和和离差平方和的概念。在回归分析中,SSR 表示聚类中类似的组间平方和概念,由预测数据与标签均值之间差值的平方和计算的出: S S R = ∑ i = 1 n ( y i ˉ − y i ^ ) 2 SSR =\sum^{n}_{i=1}(\bar{y_i}-\hat{y_i})^2 SSR=i=1∑n(yiˉ−yi^)2
- 而 SST 则是实际值和均值之间的差值的平方和计算得到: S S T = ∑ i = 1 n ( y i ˉ − y i ) 2 SST =\sum^{n}_{i=1}(\bar{y_i}-y_i)^2 SST=i=1∑n(yiˉ−yi)2
- 并且, SST 可由 SSR+SSE 计算得出。而决定系数,则由 SSR 和 SST 共同决定: R − s q u a r e = S S R S S T = S S T − S S E S S E = 1 − S S E S S T R-square=\frac{SSR}{SST}=\frac{SST-SSE}{SSE}=1-\frac{SSE}{SST} R−square=SSTSSR=SSESST−SSE=1−SSTSSE
- 很明显,决定系数是一个鉴于 [0,1] 之间的值,并且越趋近于 1,模型拟合效果越好。我们可以通过如下过程,进行决定系数的计算:
sst = np.power(labels - labels.mean(), 2).sum()
sse = SSELoss(features, w, labels)
r = 1-(sse/sst)
r
#array([[0.99998114]])
二、机器学习模型结果可信度理论与交叉验证基础
# 科学计算模块
import numpy as np
import pandas as pd
# 绘图模块
import matplotlib as mpl
import matplotlib.pyplot as plt
# 自定义模块
from ML_basic_function import *
1. 机器学习模型结果可信度理论基础与数据集划分
1.1 机器学习模型结果可信度基础理论
- 模型评估指标是用于评估模型效果好坏的数值指标,例如 SSE 就是评估回归类模型拟合效果的指标。但是否是评估指标好的模型就一定能用呢?其实并不一定。这里会涉及到一个关于评估指标可信度、或者说了解模型真实性能的重要命题。
- 其实,要了解模型的性能其实并不简单,固然我们会使用某些指标去进行模型评估,但其实指标也只是我们了解模型性能的途径而不是模型性能本身。
- 而要真实、深刻的评判模型性能,就必须首先了解机器学习的建模目标,并在此基础之上熟悉我们判断模型是否能够完成目标的一些方法,当然,只有真实了解的模型性能,我们才能进一步考虑如何提升模型性能。
- 无论是机器学习还是传统的统计分析模型,核心使命就是探索数字规律,而有监督学习则是希望在探索数字规律的基础上进一步对未来进行预测。
- 当然,在数字的世界,这个预测未来,也就是预测未来某项事件的某项数值指标,如某地区未来患病人次、具备某种数字特征的图片上的动物是哪一类,此处的未来也并非指绝对意义上的以后的时间,而是在模型训练阶段暂时未接触到的数据。
- 正是因为模型有了在未知标签情况下进行预判的能力,有监督学习才有了存在的价值,但我们知道,基本上所有的模型,都只能从以往的历史经验当中进行学习,也就是在以往的、已经知道的数据集上进行训练(如上述利用已知数据集进行模型训练,如利用过往股票数据训练时间序列模型)。
- 这里的核心矛盾在于,在以往的数据中提取出来的经验(也就是模型),怎么证明能够在接下来的数据中也具备一定的预测能力呢?或者说,要怎么训练模型,才能让模型在未知的数据集上也拥有良好的表现呢?
- 目的相同,但在具体的实现方法上,传统的数理统计分析建模和机器学习采用了不同的解决方案。
- 在统计分析领域,我们会假设现在的数据和未来的数据其实都属于某个存在但不可获得的总体,也就是说,现在和未来的数据都是从某个总体中抽样而来的,都是这个总体的样本。而正式因为这些数据属于同一个总体,因此具备某些相同的规律,而现在挖掘到的数据规律也就在某些程度上可以应用到未来的数据当中去,不过呢,不同抽样的样本之间也会有个体之间的区别,另外模型本身也无法完全捕获规律,而这些就是误差的来源。
- 虽然样本和总体的概念是统计学概念,但样本和总体的概念所假设的前后数据的局部规律一致性,却是所有机器学习建模的基础。如果获取到的数据前后描绘的不是一件事情,那么模型训练也就毫无价值(比如拿着 A 股走势预测的时间序列预测某地区下个季度患病人次)。
- 因此,无论是机器学习所强调的从业务角度出发,要确保前后数据描述的一致性,还是统计分析所强调的样本和总体的概念,都是建模的基础。
- 在有了假设基础之后,统计分析就会利用一系列的数学方法和数理统计工具去推导总体的基本规律,也就是变量的分布规律和一些统计量的取值,由于这个过程是通过已知的样本去推断未知的总体,因此会有大量的估计和检验,在确定了总体的基本分布规律之后,才能够进一步使用统计分析模型构建模型(这也就是为什么在数理统计分析领域,构建线性回归模型需要先进行一系列的检验和变换的原因)。
- 当然,这些模型都是在总体规律基础之上、根据样本具体的数值进行的建模,我们自然有理由相信这些模型对接下来仍然是从总体中抽样而来的样本还是会具备一定的预测能力,这也就是我们对统计分析模型信心的来源。
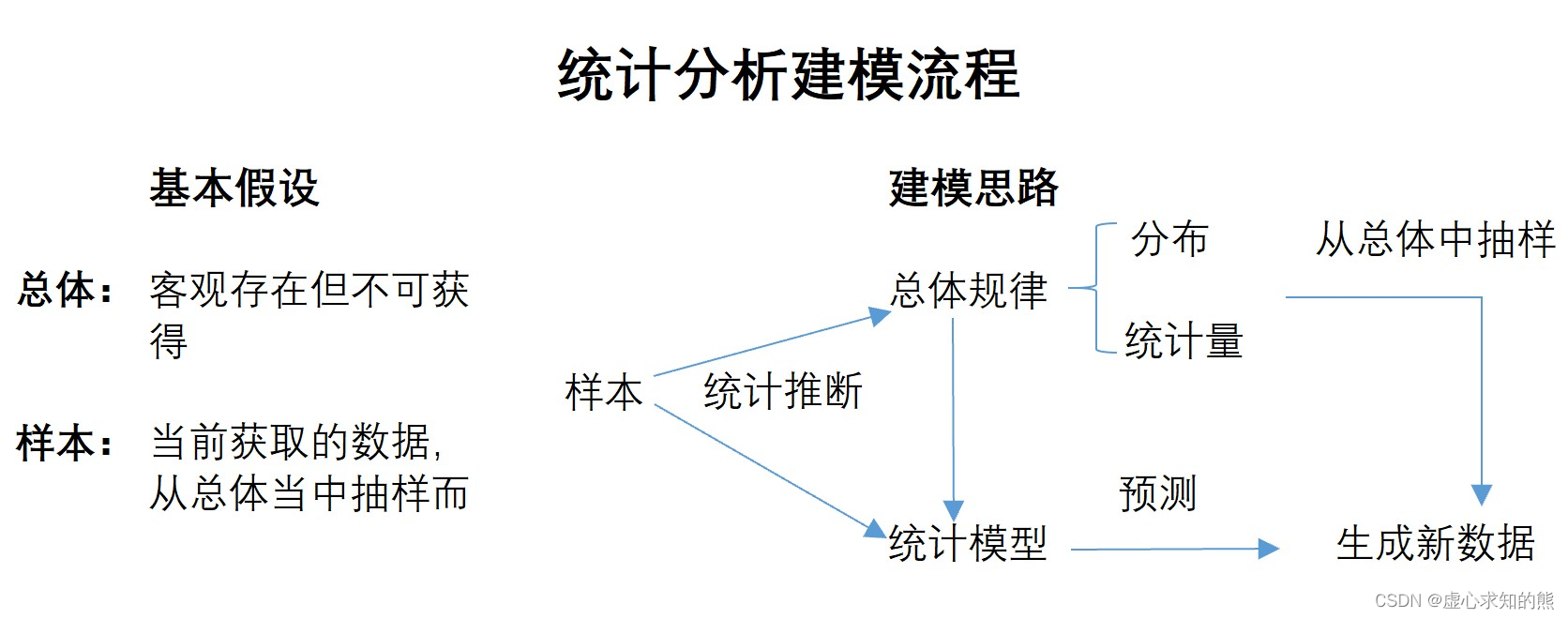
- 简单来说,就是我们通过样本推断总体的规律,然后结合总体的规律和样本的数值构建模型,由于模型也描绘了总体规律,所以模型对接下来从总体当中抽样而来的数据也会有不错的预测效果,这个过程我们可以通过下图来进行表示。
- 对于机器学习来说,并没有借助样本 - 总体的基本理论,而是简单的采用了一种后验的方法来判别模型有效性。
- 我们假设前后获取的数据拥有规律一致性,但数据彼此之间又略有不同,为了能够在捕捉规律的同时又能考虑到略有不同所带来的误差。
- 机器学习会把当前能获取到的数据划分成训练集(trainSet)和测试集(testSet),在训练集上构建模型,然后带入测试集的数据,观测在测试集上模型预测结果和真实结果之间的差异。
- 这个过程其实就是在模拟获取到真实数据之后模型预测的情况,模型能够在未知标签的数据集上进行预测,就是模型的核心价值,此时的测试集就是用于模拟未来的未知标签的数据集。
- 如果模型能够在测试集上有不错的预测效果,我们就简单粗暴的认为模型可以在真实的未来获取的未知数据集上有不错的表现。其一般过程可以由下图表示。

- 因此,我们称模型在训练集上误差称为训练误差,在测试集上的误差称为泛化误差,不过毕竟在测试集上进行测试还只是模拟演习,我们采用模型的泛化能力来描述模型在未知数据上的判别能力。
- 当然泛化能力无法准确衡量(未知的数据还未到来,到来的数据都变成了已知数据),我们只能通过模型在训练集和测试集上的表现,判别模型泛化能力,当然,最基本的,我们会通过模型在测试集上的表现来判断模型的泛化能力。
1.2 数据集切分方法
接下来,我们就尝试通过数据集切分来执行更加可信的机器学习建模流程。首先是对数据集进行切分。一般来说,为了避免数据集上下顺序对数据规律的影响,我们会考虑对数据集进行随机切分,其中 70%-80% 作为训练集、20%-30% 作为测试集。此处我们先考虑构建一个数据切分函数,用于训练集和测试集的切分:
- np.random.shuffle 函数
- 在 NumPy 中,我们可以非常便捷的通过调用 np.random.shuffle 函数来进行二维数组按行重排的相关操作,而二维数组也就是结构化数据的一般表示形式,因此我们可以使用该函数进行数据集乱序排列。
- 并且我们可以通过设置随机数种子,来复现这个乱序的过程,这将极大程度有助于当需要对多个序列进行乱序排列时的代码简化。
A = np.arange(10).reshape(5, 2)
A
#array([[0, 1],
# [2, 3],
# [4, 5],
# [6, 7],
# [8, 9]])
B = np.arange(0, 10, 2).reshape(-1, 1) #(-1, 1)表示为设定行数,1列
B
#array([[0],
# [2],
# [4],
# [6],
# [8]])
np.random.seed(24)
np.random.shuffle(A) #shuffle表示打乱
A
#array([[8, 9],
# [2, 3],
# [0, 1],
# [6, 7],
# [4, 5]])
B
#array([[0],
# [2],
# [4],
# [6],
# [8]])
np.random.seed(24)
np.random.shuffle(B)
B
#array([[8],
# [2],
# [0],
# [6],
# [4]])
- np.vsplit 切分函数
- 此外,我们可以通过 vsplit 函数进行数组的按行切分,也就相当于 split(axis=0)。
A
#array([[8, 9],
# [2, 3],
# [0, 1],
# [6, 7],
# [4, 5]])
# 从行索引的第二、三元素之间切开
np.vsplit(A,[2, ])
#[array([[8, 9],
# [2, 3]]),
# array([[0, 1],
# [6, 7],
# [4, 5]])]
- 数据集切分函数
- 基于上述函数,我们可以非常简单的构建一个数据集切分函数:
def array_split(features, labels, rate=0.7, random_state=24):
"""
训练集和测试集切分函数
:param features: 输入的特征张量
:param labels:输入的标签张量
:param rate:训练集占所有数据的比例
:random_state:随机数种子值
:return Xtrain, Xtest, ytrain, ytest:返回特征张量的训练集、测试集,以及标签张量的训练集、测试集
"""
np.random.seed(random_state)
np.random.shuffle(features) # 对特征进行切分
np.random.seed(random_state)
np.random.shuffle(labels) # 按照相同方式对标签进行切分
num_input = len(labels) # 总数据量
split_indices = int(num_input * rate) # 数据集划分的标记指标
Xtrain, Xtest = np.vsplit(features, [split_indices, ])
ytrain, ytest = np.vsplit(labels, [split_indices, ])
return Xtrain, Xtest, ytrain, ytest
- 一般来说,训练集和测试集可以按照 8:2 或 7:3 比例进行划分。
- 在进行数据划分的过程中,如果测试集划分数据过多,参与模型训练的数据就会相应减少,而训练数据不足则会导致模型无法正常训练、损失函数无法收敛、模型过拟合等问题。
- 如果测试集划分数据过少,则无法代表一般数据情况测试模型是否对未知数据也有很好的预测作用。因此,根据经验,我们一般来说会按照 8:2 或 7:3 比例进行划分。
- 测试函数性能
f = np.arange(10).reshape(-1, 1) # 创建特征0-9
f
#array([[0],
# [1],
# [2],
# [3],
# [4],
# [5],
# [6],
# [7],
# [8],
# [9]])
l = np.arange(1, 11).reshape(-1, 1) # 创建标签1-10,保持和特征+1的关系
l
#array([[ 1],
# [ 2],
# [ 3],
# [ 4],
# [ 5],
# [ 6],
# [ 7],
# [ 8],
# [ 9],
# [10]])
array_split(f, l)
#(array([[9],
# [4],
# [8],
# [7],
# [5],
# [6],
# [1]]),
# array([[0],
# [3],
# [2]]),
# array([[10],
# [ 5],
# [ 9],
# [ 8],
# [ 6],
# [ 7],
# [ 2]]),
# array([[1],
# [4],
# [3]]))
1.3 线性回归手动实现
- 根据机器学习结果可信度理论,我们构建一个在训练集上训练、在测试集上测试的完整的线性回归实现流程。
- 数据准备
# 设置随机数种子
np.random.seed(24)
# 扰动项取值为0.01
features, labels = arrayGenReg(delta=0.01)
# 数据切分
Xtrain, Xtest, ytrain, ytest = array_split(features, labels)
- 在训练集上训练
- 最小二乘法求解公式: w ^ = ( X T X ) − 1 X T y \hat w = (X^TX)^{-1}X^Ty w^=(XTX)−1XTy
w = np.linalg.inv(Xtrain.T.dot(Xtrain)).dot(Xtrain.T).dot(ytrain)
w
#array([[ 1.99976073],
# [-0.99986178],
# [ 0.99934303]])
- 在大多数情况下,所谓训练模型,都是训练得出模型的一组参数。
- 在测试集上测试
- 然后即可在测试集上计算模型评估指标:
SSELoss(Xtest, w, ytest)
array([[0.02725208]])
- 至此,我们即完成了模型在训练集上训练得出参数,然后运行测试集观察结果的全过程。由于数据情况较为简单,因此模型效果较好。
- 但如果测试集效果不好,我们能否因此对模型进行调整的呢?如果测试集真的完全不参与建模,那么根据测试集反馈结果调整模型是否算测试集间接参与建模?如果测试集不能间接参与建模,那测试集的提供的模型结果反馈又有什么作用呢?这就是所谓的,测试集悖论。
1.4 测试集的不可知悖论
- 我们已经知道,机器学习模型主要通过模型在测试集上的运行效果来判断模型好坏,测试集相当于是高考,而此前的模型训练都相当于是在练习,但怎么样的练习才能有效的提高高考成绩?
- 这里就存在一个悖论,那就是练习是为了高考,而在高考前我们永远不知道练习是否有效,那高考对于练习的核心指导意义何在?
- 在机器学习领域,严格意义上的测试集是不能参与建模的,此处不能参与建模,不仅是指在训练模型时不能带入测试集进行训练,更是指当模型训练完成之后、观察模型在测试集上的运行结果后,也不能据此再进行模型修改(比如增加神经网络层数)。
- 把数据带入模型训练是影响模型参数,而根据模型运行结果再进行模型结构调整,实际上是修改了模型超参数,不管是修改参数还是超参数,都是影响了模型建模过程,都相当于是带入进行了建模。
- 如果通过观察测试集结果再调整模型结构,也相当于是带入测试集数据进行训练,而严格意义上的测试集,是不能带入模型训练的。
- 但是,学习建模的核心目标就是提升模型的泛化能力。而泛化能力指的是在模型未知数据集(没带入进行训练的数据集)上的表现,虽然测试集只能测一次,但我们还是希望有机会能把模型带入未知数据集进行测试,此时我们就需要一类新的数据集——验证集。
- 验证集在模型训练阶段不会带入模型进行训练,但当模型训练结束之后,我们会把模型带入验证集进行计算,通过观测验证集上模型运行结果,判断模型是否要进行调整,验证集也会模型训练,只不过验证集训练的不是模型参数,而是模型超参数。
- 因此,我们也可以把验证集看成是应对高考的模拟考试,通过“模拟考试”的考试结果来调整复习策略,从而更好的应对高考。
- 总的来说,测试集是严格不能带入训练的数据集,在实际建模过程中我们可以先把测试集切分出来,然后假装这个数据集不存在,在剩余的数据集中划分训练集和验证集,把训练集带入模型进行运算,再把验证集放在训练好的模型中进行运行,观测运行结果,再进行模型调整。
- 因此,在模型训练和观测模型运行结果的过程总共涉及三类数据集,分别是训练集、验证集和测试集。不过由于测试集定位特殊,在一些不需要太严谨的场景下,有时也会混用验证集和测试集的概念。
- 在不区分验证集和测试集的情况下,当数据集切分完成后,对于一个模型来说,我们能够获得两套模型运行结果,一个是训练集上模型效果,一个是测试集上模型效果,而这组结果,就将是整个模型优化的基础数据。
2. 交叉验证基本思想
- 除了训练集-测试集划分理论之外,和模型结果可信度相关的,还有一个基本理论——交叉验证。
- 尽管通过训练集和测试集的划分,我们可以以不参与建模的测试集的结论来证明模型结果的可信度,但在很多实际场景中,数据集的随机切分本身也是影响模型泛化能力、影响测试集结果可信度的重要因素。
- 此时,我们可以采用一种名为交叉验证的技术手段来进一步提升模型最终输出结果的可信度。
- 交叉验证的基本思想非常简单,在我们不严格区分测试集的情况下,我们可以将数据集整体按照某个比例切分,然后进行循环验证。
- 在所有的切分方法中,最基础也最常用的一种就是所谓的 K-fold(K折)验证,也就是将数据集进行 K 份等比例划分,然后依次取出其中一份进行验证(测试)、剩下几份进行训练。
- 例如,当我们使用 10 折验证时,数据集划分情况如下所示:

- 假设仍然是此前我们创建的数据集并且仍然采用 SSE 作为模型评估指标,则在进行十折验证时可以计算出十组 SSE 取值,最终我们可以对这十组结果进行均值计算,求得这组参数最终所对应的模型评估指标结果。
- 不过此时我们需要在所有的数据集上进行训练,然后再进行交叉验证。