数学知识(三)
这一小节讲的是高斯消元,组合数。
高斯消元
高斯消元是用来解方程的,通常来说可以在
O
(
n
3
)
O(n^3)
O(n3) 的时间复杂度内,求出包含 n 个未知数的,n个方程的多元线性方程组的解。如下的方程组就称为多元线性方程组
a 11 x 1 + a 12 x 2 + . . . + a 1 n x n = b 1 a_{11}x_1+a_{12}x_2+...+a_{1n}x_n=b_1 a11x1+a12x2+...+a1nxn=b1
a 21 x 1 + a 22 x 2 + . . . + a 2 n x n = b 2 a_{21}x_1+a_{22}x_2+...+a_{2n}x_n=b_2 a21x1+a22x2+...+a2nxn=b2
a 31 x 1 + a 32 x 2 + . . . + a 3 n x n = b 3 a_{31}x_1+a_{32}x_2+...+a_{3n}x_n=b_3 a31x1+a32x2+...+a3nxn=b3
…
a n 1 x 1 + a n 2 x 2 + . . . + a n n x n = b n a_{n1}x_1+a_{n2}x_2+...+a_{nn}x_n=b_n an1x1+an2x2+...+annxn=bn
多元线性方程组的解,通常有三种情况:无解;有唯一解;有无穷组解。
上面的方程组,可以将其系数提取出来,形成系数矩阵,并在最右侧添加常数列,形成增广矩阵,即
[ a 11 , a 12 , . . . , a 1 n , b 1 ] [a_{11},a_{12},...,a_{1n},b_1] [a11,a12,...,a1n,b1]
[ a 21 , a 22 , . . . , a 2 n , b 2 ] [a_{21},a_{22},...,a_{2n},b_2] [a21,a22,...,a2n,b2]
…
[ a n 1 , a n 2 , . . . , a n n , b n ] [a_{n1},a_{n2},...,a_{nn},b_n] [an1,an2,...,ann,bn]
而矩阵具有三种初等行列变换
- 把某一行乘以一个非零的数
- 交换某2行
- 把某行的若干倍加到另一行上
这三种变换,不会影响方程组的解
高斯消元,可以用某种统一的步骤,通过执行上面的初等行列变换,使得方程组的系数矩阵,变成一个倒三角形的矩阵。即变成
a 11 x 1 + . . . + a 1 n x n = b 1 a_{11}x_1+...+a_{1n}x_n=b_1 a11x1+...+a1nxn=b1
a 22 x 2 + . . . + a 2 n x n = b 2 a_{22}x_2+...+a_{2n}x_n=b_2 a22x2+...+a2nxn=b2
…
a n n x n = b n a_{nn}x_n=b_n annxn=bn
从最后一个方程能直接求出 x n x_n xn,依次可以往上求解出 x n − 1 x_{n-1} xn−1, x n − 2 x_{n-2} xn−2,…, x 1 x_1 x1
当执行完高斯消元后,如果得到的方程组,是
-
完美的阶梯型(第一行有n个未知数,第二行有n-1个未知数,最后一行有1个未知数)
即一共有
n个有效方程,此时有唯一解 -
得到的方程组中有形如
0=非零的此时无解
-
得到的方程组中有形如
0=0的(这种方程是可以被其他方程表示的,是多余的无效方程)即有效方程的个数小于
n,此时有无穷组解
高斯消元的算法步骤如下
枚举每一列(第c列)
- 找到当前这一列系数绝对值最大的一行(从剩余的行中找)
- 将该行交换到最上面(不是交换到第一行,而是交换到剩余行中最上面的一行)
- 将该行的该列的系数变成1
- 使用该行,对所有剩余行进行消元,将该列消成0
注意,每次遍历,找到当前列的绝对值最大的那一行,处理完毕后,后续的处理只针对剩余的行。
练习题:acwing - 883: 高斯消元解线性方程组
#include <iostream>
#include <cmath>
using namespace std;
const int N = 110;
double a[N][N];
int n;
double eps = 1e-8;
int solve() {
int c = 0, r = 0;
for (; c < n; c++) {
// 每轮循环消掉一列
int t = r;
// 先找到当前需要处理的列的最大系数的那一行
for (int i = r + 1; i < n; i++) {
if (fabs(a[i][c]) > fabs(a[t][c])) t = i;
}
// 当前列的最大系数为0, 则不用处理
if (fabs(a[t][c]) < eps) continue;
// 将最大系数的行交换到最上面来
for (int i = c; i <= n; i++) swap(a[t][i], a[r][i]);
// 将该列系数化为1
for (int i = n; i >= c; i--) a[r][i] /= a[r][c];
// 用该行消掉下面所有行的该列
for (int i = r + 1; i < n; i++) {
for (int j = n; j >= c; j--) {
a[i][j] -= a[r][j] * a[i][c];
}
}
// 有效方程数+1
r++;
}
if (r < n) {
// 有效方程数 < n, 可能是无解或无穷多解
for (int i = r; i < n; i++) {
if (fabs(a[i][n]) > eps) return 0; // 无解
}
return 2; // 无穷多解
} else {
// 唯一解
for (int i = n - 1; i >= 0; i--) {
for (int j = n - 1; j > i; j--) {
a[i][n] -= a[i][j] * a[j][n];
}
}
return 1;
}
}
int main() {
std::ios::sync_with_stdio(false);
cin >> n;
for (int i = 0; i < n; i++) {
for (int j = 0; j <= n; j++) {
cin >> a[i][j];
}
}
int res = solve();
if (res == 0) printf("No solution\n");
else if (res == 2) printf("Infinite group solutions\n");
else {
for (int i = 0; i < n; i++) {
if (fabs(a[i][n]) < eps) a[i][n] = 0;
printf("%.2lf\n", a[i][n]);
}
}
return 0;
}
对上面的代码略加解释:
最外圈的循环是针对列而言的,从左到右枚举0到n-1列(这些列都是方程组中的未知数的系数,第n列是某一个方程组右侧的常数)。
最外圈的循环每进行一次,就能够消掉一个未知数(消掉一个元)。
循环的内部,先是从剩余的行(r行及其下面的行)中找到当前列系数绝对值最大的那一行(若当前列系数最大的都是0,则说明当前列无需进行消元了,直接continue,继续处理下一列);随后,将这一行交换到最上方(交换到r行);接着,将这一行当前列的系数化为1(注意代码中是从右往左处理的,因为处理时需要用到最左侧的那一列,若从左往右处理,则最左侧的列一开始就会被更新,从而影响右侧列的更新);最后,遍历剩余行,将剩余行减掉当前行的某一个倍数,使得能够消掉当前列。最后,将r加一,表示该行处理完毕,接下来的处理都针对该行下面的行。
循环结束后,r的值就是最后得到的有效方程的个数。若每次循环都能恰好消去一个元,则r最后就等于n,此时得到的方程组就是一个完美的阶梯型(从上往下,第一个方程有n个未知数,最后一个方程有1个未知数)。此时方程组有唯一解。
若r小于n,则说明方程组中有些方程是无效的。并且,r还没走到最后一行时,就已经处理到了最后一列(已经消元结束)。此时需要对r以下的行,进行判断。r以下的行,由于消元结束,都不再包含未知数了,所以这些行的0到n-1列(未知数的系数)应当都为0,此时需要判断第n列的常数。若这个常数为0,则方程就是0=0,无效方程;若这个常数不为0,则这个方程本身就矛盾了,所以整个方程组无解。
当方程有唯一解时。我们从最后一个方程往上递推,可以依次求解出每个未知数的值。
需要注意,由于我们在消元的过程中,对每个未知数的系数,都化简成了1。则消元结束后,最后一行应当是 x n = c x_n=c xn=c
即消元结束后最后一行的常数列,直接就是未知数 x n x_n xn 的解了。我们依次带入上面的行,即可求出其他的未知数的解。
这一部分也是整个高斯消元的代码中最难以理解的部分,单独拎出来说。
for(int i = n - 1; i >= 0; i--) {
for(int j = i + 1; j < n; j++) {
a[i][n] -= a[i][j] * a[j][n];
}
}
最后,每个未知数的解,我们都是保存在最右侧的常数列上面的。
针对第i行,我们需要解出
x
i
x_i
xi
比如我们化简后得到的方程组如下
x 0 + 1.5 x 1 + 2 x 2 = 7.5 x_0+1.5x_1+2x_2=7.5 x0+1.5x1+2x2=7.5
x 1 + 0.5 x 2 = 3.5 x_1+0.5x_2=3.5 x1+0.5x2=3.5
x 2 = 4 x_2 = 4 x2=4
一共3个方程组,我们枚举从第2行到第0行。
即,n=3,我们枚举i,从2到0
i=2时,j从3开始,发现j < n,则直接结束;
i=1时,j从2开始,我们计算 a[1][3] -= a[1][2] * a[2][3],即相当于把
x
1
+
0.5
x
2
=
3.5
x_1+0.5x_2=3.5
x1+0.5x2=3.5 移向,变成
x
1
=
3.5
−
0.5
x
2
x_1=3.5-0.5x_2
x1=3.5−0.5x2
i=0时,j从1开始,先把
1.5
x
1
1.5x_1
1.5x1 减掉,
x
1
x_1
x1 的值直接取下一行的常数列 a[1][3];随后 j=2,再尝试把
2
x
2
2x_2
2x2 减掉,
x
2
x_2
x2 的值直接取第2行的常数列 a[2][3]。
我们可以发现,从最后一行往上计算,每一行的常数列其实都是某个未知数的解。
比如最后一行的常数列,一定是最后一个未知数的解;倒数第二行的常数列,是倒数第二个未知数的解。
更一般的,在我们循环到第 i 行时,其实需要求解的就是
x
i
x_i
xi。而这一行中,还有剩下的
x
i
+
1
x_{i+1}
xi+1 到
x
n
−
1
x_{n-1}
xn−1 个未知数需要消掉,这些未知数的解,在先前求解 i 下面的行时,已经求解了出来(是i下面那些行的常数列)。所以我们遍历
j
∈
[
i
+
1
,
n
−
1
]
j \in [i+1,n-1]
j∈[i+1,n−1],依次消掉这些未知数,即用这一行的常数列 a[i][n] 来依次 减掉
x
i
+
1
x_{i+1}
xi+1 到
x
n
−
1
x_{n-1}
xn−1 这些未知数的项即可。
对于
j
∈
[
i
+
1
,
n
−
1
]
j \in [i+1,n-1]
j∈[i+1,n−1],
x
j
x_j
xj 就是先前已经求解出来的第
j
j
j 行的常数列,即 a[j][n],它的系数就是a[i][j]。所以只需要减掉
a[i][j] * a[j][n] 即可。
所以,我们处理某一行 i,求解
x
i
x_i
xi 时,只需要用这一行的常数列 a[i][n],依次减掉
x
j
x_j
xj (
j
∈
[
i
+
1
,
n
−
1
]
j \in [i+1,n-1]
j∈[i+1,n−1])这些项。而某个未知数
x
j
x_j
xj 的值为 a[j][n],系数为 a[i][j]。所以更新的公式就是 a[i][n] -= a[i][j] * a[j][n]
最后,所有行的常数列,就是方程组的解。即
x
0
x_0
x0 = a[0][n],
x
1
x_1
x1 = a[1][n],…,
x
n
−
1
x_{n-1}
xn−1 = a[n-1][n]
扩展练习题:高斯消元解异或线性方程组
#include <iostream>
using namespace std;
const int N = 110;
int a[N][N];
int n;
int solve() {
int c = 0, r = 0;
for (; c < n; c++) {
// 找到第一个系数非0的列
int t = -1;
for (int i = r; i < n; i++) {
if (a[i][c] == 1) {
t = i;
break;
}
}
if (t == -1) continue;
// 交换到最上方
for (int i = c; i <= n; i++) swap(a[t][i], a[r][i]);
// 消掉下面方程的该列
for (int i = r + 1; i < n; i++) {
// 只有系数同样为1时才能消掉
if (a[i][c] == 0) continue;
for (int j = c; j <= n; j++) {
a[i][j] = a[r][j] ^ a[i][j];
}
}
r++;
}
if (r < n) {
for (int i = r; i < n; i++) {
if (a[i][n]) return 0;
}
return 2;
} else {
for (int i = n - 1; i >= 0; i--) {
for (int j = n - 1; j > i; j--) {
// 只有系数为1时, 需要异或上这个值
if (a[i][j]) a[i][n] ^= a[j][n];
}
}
return 1;
}
}
int main() {
std::ios::sync_with_stdio(false);
cin >> n;
for (int i = 0; i < n; i++) {
for (int j = 0; j <= n; j++) {
cin >> a[i][j];
}
}
int res = solve();
if (res == 0) printf("No solution\n");
else if (res == 2) printf("Multiple sets of solutions\n");
else {
for (int i = 0; i < n; i++) {
printf("%d\n", a[i][n]);
}
}
return 0;
}
组合数
求组合数有很多种方式,需要根据数据范围来选择使用哪种方式。
递推
对于组合数 C a b C_a^b Cab 可以用一个递推式来表达,即 C a b = C a − 1 b + C a − 1 b − 1 C_a^b = C_{a-1}^b+C_{a-1}^{b-1} Cab=Ca−1b+Ca−1b−1
所以每个组合数 C a b C_a^b Cab 都可以用更小的组合数来表示
这样我们就可以根据上面的递推式,预处理出数据范围内全部的组合数,查询时,直接查表即可。
针对递推式 C a b = C a − 1 b + C a − 1 b − 1 C_a^b = C_{a-1}^b+C_{a-1}^{b-1} Cab=Ca−1b+Ca−1b−1 的一种通俗的解释:
考虑一个口袋里一共有 a a a 个苹果🍎,我们从中选 b b b 个苹果,则总共的选法就是 C a b C_a^b Cab,我们考虑将其中一个苹果打上标记(比如称其为金苹果)。那么总共的选法可以分为2大类:包含这个金苹果;不包含这个金苹果。
包含这个金苹果的选法,则是从余下的苹果中,再选 b − 1 b-1 b−1 个,即 C a − 1 b − 1 C_{a-1}^{b-1} Ca−1b−1
不包含这个金苹果的选法,则是从余下的苹果中,再选 b b b 个,即 C a − 1 b C_{a-1}^{b} Ca−1b
所以 C a b = C a − 1 b + C a − 1 b − 1 C_a^b = C_{a-1}^{b} + C_{a-1}^{b-1} Cab=Ca−1b+Ca−1b−1
练习题:acwing - 885: 求组合数I
数据范围:1 <= n <= 10000, 1 <= b <= a <= 2000
#include <iostream>
using namespace std;
const int MOD = 1e9 + 7;
const int N = 2010;
int c[N][N];
void init() {
for(int i = 0; i < N; i++) {
for(int j = 0; j <= i; j++) {
if(j == 0) c[i][j] = 1;
else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % MOD;
}
}
}
int main() {
int n;
cin >> n;
init();
while(n--) {
int a, b;
cin >> a >> b;
cout << c[a][b] << endl;
}
}
需要注意,上面预处理时,i需要从0开始,需要算出
C
0
0
=
1
C_0^0=1
C00=1,而针对
C
a
b
C_a^b
Cab ,当
b
>
a
b \gt a
b>a 的情况,不用处理,因为数组初始化为0。比如
C 5 5 = C 4 5 + C 4 4 = 0 + 1 C_5^5 = C_4^5+C_4^4=0+1 C55=C45+C44=0+1
递推法的复杂度是
O
(
n
2
)
O(n^2)
O(n2),对于这道题的数据范围,计算量就是2000^2 = 4 × 10^6
预处理阶乘
组合数的公式为 C a b = a ! ( a − b ) ! × b ! C_a^b = \frac{a!}{(a-b)! × b!} Cab=(a−b)!×b!a!
需要的都是某个数的阶乘,那么我们把所有数的阶乘预处理一下,阶乘数组用fact来表示,即fact[i] = i! mod 10^9 + 7。
同时我们注意到,阶乘项也出现在分母中,而由于我们需要对结果取一个模,所以我们可以对i的阶乘,求一下乘法逆元。把除法转化为乘法。某个数的阶乘在模10^9 + 7下的乘法逆元,我们用infact[i]来表示。
于是用这两个预处理出的数组,就能在 O ( 1 ) O(1) O(1) 时间内求出任意的组合数。
由于模的10^9 - 7是个质数,所以我们求乘法逆元可以直接用欧拉定理的特例,费马小定理进行求解。
注:若a和m互质,求a mod m下的乘法逆元时,若m是质数,则用快速幂进行求解,乘法逆元为ap-2;若m不是质数,则用扩展欧几里得算法进行求解 ,就不要傻乎乎的先对m求个欧拉函数,再用欧拉定理做幂运算来求解,太慢了。
设a-1 为逆元,则有 a × a-1 mod m = 1,那么有a × a-1 = km + 1,移项一下就是 a× a-1 - km = 1。我们将a-1用x替换,m用b替换,-k用y替换,则就是 ax + by = 1,其中a和b是固定的,未知数是x和y。我们需要求解的逆元就是x,而a和b是互质的,所以gcd(a,b) = 1,根据裴蜀定理,这个二元线性方程一定有解,并且能用扩展欧几里得算法进行求解。
练习题:acwing - 886: 求组合数II
数据范围:1 <= n <= 10000,1 <= b <= a <= 10^5
#include <iostream>
typedef long long LL;
using namespace std;
const int N = 100010, MOD = 1e9 + 7;
LL fac[N], infac[N];
int qmi(int a, int b, int p) {
int res = 1;
while (b) {
if (b & 1) res = (LL)res * a % p;
a = (LL)a * a % p;
b >>= 1;
}
return res;
}
void init() {
fac[0] = infac[0] = 1;
for (int i = 1; i < N; i++) {
fac[i] = fac[i - 1] * i % MOD;
infac[i] = infac[i - 1] * qmi(i, MOD - 2, MOD) % MOD;
}
}
int main() {
std::ios::sync_with_stdio(false);
init();
int n, a, b;
cin >> n;
while (n--) {
cin >> a >> b;
LL res = fac[a] * infac[a - b] % MOD * infac[b] % MOD;
printf("%lld\n", res);
}
return 0;
}
对于预处理时,求解fact和 infact数组时,
fact[i] = fact[i - 1] * i 这个很好理解,但是逆元数组 infact的递推怎么理解呢?
可以这样想,对于阶乘 a ! a! a! ,其逆元为 ( a ! ) − 1 (a!)^{-1} (a!)−1,有 a ! × ( a ! ) − 1 ≡ 1 m o d P a! \times (a!)^{-1} \equiv 1 \mod P a!×(a!)−1≡1modP
对于阶乘 ( a + 1 ) ! (a + 1)! (a+1)!,我们将其拆分为 a ! × ( a + 1 ) a! \times (a + 1) a!×(a+1),则有 a ! × ( a + 1 ) × ( a ! ) − 1 × x ≡ 1 m o d P a! \times (a + 1) \times (a!)^{-1} \times x \equiv 1 \mod P a!×(a+1)×(a!)−1×x≡1modP
则 ( a + 1 ) ! (a + 1)! (a+1)! 的逆元为 ( a ! ) − 1 × x (a!)^{-1} \times x (a!)−1×x,根据模运算的特性,我们将上式进行一下组合变换,有
- a ! × ( a ! ) − 1 ≡ 1 m o d P a! \times (a!)^{-1} \equiv 1 \mod P a!×(a!)−1≡1modP
- ( a + 1 ) × x ≡ 1 m o d P (a + 1) \times x \equiv 1 \mod P (a+1)×x≡1modP
那么很明显的, x = ( a + 1 ) − 1 x = (a + 1)^{-1} x=(a+1)−1
也就是说,我们只需要求解一下 a + 1 a + 1 a+1的逆元
于是就能得到 infact数组的递推式:
i
n
f
a
c
t
[
a
+
1
]
=
i
n
f
a
c
t
[
a
]
×
(
a
+
1
)
−
1
infact[a + 1] = infact[a] \times (a+1)^{-1}
infact[a+1]=infact[a]×(a+1)−1
预处理出2个阶乘数组,时间复杂度为
O
(
n
)
O(n)
O(n),实际性能瓶颈在于计算 infact[i]时,需要使用快速幂计算 i 的 MOD - 2次方,需要的复杂度是
O
(
log
M
O
D
)
O(\log MOD)
O(logMOD),而本题的 MOD = 10^9 + 7,log MOD大概等于30,所以实际上复杂度是 30n
注意,只有在模数
p
p
p 为质数,并且
a
a
a 和
b
b
b 都小于
p
p
p 时,才能用预处理阶乘的方式求解。若
a
>
p
a > p
a>p,则可能 [1, a]中有的数和 p 不互质,不互质的话,就不存在乘法逆元。
卢卡斯定理
参考:
-
https://zhuanlan.zhihu.com/p/452976974
-
https://www.cnblogs.com/onlyblues/p/15339937.html
-
https://blog.csdn.net/qq_40679299/article/details/80489761
-
https://zhuanlan.zhihu.com/p/116698264
定义:
对于非负整数 a a a, b b b 和质数 p p p,有 C a b ≡ ∏ i = 0 k C a i b i m o d p C_a^b \equiv \prod_{i=0}^kC_{a_i}^{b_i} \space \mod p Cab≡∏i=0kCaibi modp,其中
a = a k p k + a k − 1 p k − 1 + . . . + a 1 p + a 0 a = a_kp^k+a_{k-1}p^{k-1} + ... + a_1p+a_0 a=akpk+ak−1pk−1+...+a1p+a0, b = b k p k + b k − 1 p k − 1 + . . . + b 1 p + b 0 b = b_kp^k+b_{k-1}p^{k-1}+...+b_1p+b_0 b=bkpk+bk−1pk−1+...+b1p+b0
一般,使用的是下面的式子
C a b ≡ C a m o d p b m o d p × C a / p b / p ( m o d p ) C_a^b ≡ C_{a \mod p}^{b \mod p} × C_{a / p}^{b / p} (\mod p) Cab≡Camodpbmodp×Ca/pb/p(modp),其中 p p p 为质数
证明:
-
引理1:对于组合数 C p i C_p^i Cpi,其中 p p p 为质数,始终满足 C p i ≡ 0 ( m o d p ) ( 0 < i < p ) C_p^i \equiv 0 (\mod p) \space \space (0 < i < p) Cpi≡0(modp) (0<i<p)
这个引理很好证明,根据组合数公式,有 C p i = p × ( p − 1 ) × . . . × ( p − i + 1 ) i ! C_p^i = \frac{p \times(p-1) \times ... \times (p-i+1)}{i!} Cpi=i!p×(p−1)×...×(p−i+1),而 p p p 是质数,其只存在 1 1 1 和 p p p 两个因子,所以分子中的 p p p 一定不会被消去,故计算出的结果一定是 p p p 的某个倍数,故其在 m o d p \mod p modp 下为 0 0 0
-
引理2:对于整数 x x x 和质数 p p p,始终满足 ( 1 + x ) p ≡ ( 1 + x p ) m o d p (1+x)^p \equiv (1 + x^p) \mod p (1+x)p≡(1+xp)modp
对 ( 1 + x ) p (1+x)^p (1+x)p进行二项式展开,得到 C p 0 x 0 + C p 1 x + C p 2 x 2 + . . . + C p p x p C_p^0x^0 + C_p^1x + C_p^2x^2 + ... + C_p^px^p Cp0x0+Cp1x+Cp2x2+...+Cppxp,根据引理1,中间项在 m o d p \mod p modp下都为0,可以消去,最后得到 1 + x p 1 + x^p 1+xp
-
Lucas定理
我们先将 a a a 和 b b b 转换为对应的 p p p 进制数,即
-
a = a k p k + a k − 1 p k − 1 + . . . + a 1 p + a 0 a = a_kp^k+a_{k-1}p^{k-1} + ... + a_1p+a_0 a=akpk+ak−1pk−1+...+a1p+a0
-
b = b k p k + b k − 1 p k − 1 + . . . + b 1 p + b 0 b = b_kp^k+b_{k-1}p^{k-1}+...+b_1p+b_0 b=bkpk+bk−1pk−1+...+b1p+b0
接着,有
KaTeX parse error: {align*} can be used only in display mode.
即 ( 1 + x ) a = ( 1 + x p k ) a k ⋅ ( 1 + x p k − 1 ) a k − 1 ⋅ . . . ⋅ ( 1 + x ) a 0 m o d p (1+x)^a = (1+x^{p^k})^{a_k} \cdot (1+x^{p^{k-1}})^{a_{k-1}} \cdot ... \cdot (1+x)^{a_0} \space \mod p (1+x)a=(1+xpk)ak⋅(1+xpk−1)ak−1⋅...⋅(1+x)a0 modp
根据二项式展开,容易知道 C a b C_a^b Cab 就是 ( 1 + x ) a (1+x)^a (1+x)a 展开式中的 x b x^b xb 的系数,而在上述等式右侧中,就是要知道 x b k p k + b k − 1 p k − 1 + . . . + b 0 x^{b_kp^k+b_{k-1}p^{k-1}+...+b_0} xbkpk+bk−1pk−1+...+b0 的系数。
对于等式右侧的方程 ( 1 + x p k ) a k ⋅ ( 1 + x p k − 1 ) a k − 1 ⋅ . . . ⋅ ( 1 + x ) a 0 (1+x^{p^k})^{a_k} \cdot (1+x^{p^{k-1}})^{a_{k-1}} \cdot ... \cdot (1+x)^{a_0} (1+xpk)ak⋅(1+xpk−1)ak−1⋅...⋅(1+x)a0 ,
- C a 0 b 0 C_{a_0}^{b_0} Ca0b0 即为 ( 1 + x ) a 0 (1+x)^{a_0} (1+x)a0 中 x b 0 x^{b_0} xb0 的系数
- C a 1 b 1 C_{a_1}^{b_1} Ca1b1 即为 ( 1 + x p ) a 1 (1+x^p)^{a_1} (1+xp)a1 中 x b 1 p x^{b_1p} xb1p 的系数
- …
- C a k b k C_{a_k}^{b_k} Cakbk 即为 ( 1 + x p k ) a k (1+x^{p^k})^{a_k} (1+xpk)ak 中 x b k p k x^{b_kp^k} xbkpk 的系数
将 C a 0 b 0 x b 0 C_{a_0}^{b_0}x^{b_0} Ca0b0xb0, C a 1 b 1 x b 1 p C_{a_1}^{b_1}x^{b_1p} Ca1b1xb1p, C a 2 b 2 x b 2 p 2 C_{a_2}^{b_2}x^{b_2p^2} Ca2b2xb2p2,…, C a k b k x b k p k C_{a_k}^{b_k}x^{b_kp^k} Cakbkxbkpk 乘起来,得到 C a 0 b 0 C a 1 b 1 . . . C a k b k ⋅ x b 0 x b 1 p . . . x b k p k = C a 0 b 0 C a 1 b 1 . . . C a k b k ⋅ x b C_{a_0}^{b_0}C_{a_1}^{b_1}...C_{a_k}^{b_k} \cdot x^{b_0}x^{b_1p}...x^{b_kp^k} = C_{a_0}^{b_0}C_{a_1}^{b_1}...C_{a_k}^{b_k} \cdot x^b Ca0b0Ca1b1...Cakbk⋅xb0xb1p...xbkpk=Ca0b0Ca1b1...Cakbk⋅xb
所以右式中 x b x^b xb 的系数为 C a 0 b 0 C a 1 b 1 . . . C a k b k C_{a_0}^{b_0}C_{a_1}^{b_1}...C_{a_k}^{b_k} Ca0b0Ca1b1...Cakbk,所以有 C a b ≡ C a 0 b 0 C a 1 b 1 . . . C a k b k m o d p C_a^b \equiv C_{a_0}^{b_0}C_{a_1}^{b_1}...C_{a_k}^{b_k} \mod p Cab≡Ca0b0Ca1b1...Cakbkmodp
为了将 C a b ≡ C a 0 b 0 C a 1 b 1 . . . C a k b k m o d p C_a^b \equiv C_{a_0}^{b_0}C_{a_1}^{b_1}...C_{a_k}^{b_k} \mod p Cab≡Ca0b0Ca1b1...Cakbkmodp 转化为这样的形式: C a b ≡ C a m o d p b m o d p × C a / p b / p m o d p C_a^b ≡ C_{a \mod p}^{b \mod p} × C_{a / p}^{b / p} \space \mod p Cab≡Camodpbmodp×Ca/pb/p modp
我们先把 C a 0 b 0 C a 1 b 1 . . . C a k b k C_{a_0}^{b_0}C_{a_1}^{b_1}...C_{a_k}^{b_k} Ca0b0Ca1b1...Cakbk 拆分成 C a 0 b 0 C_{a_0}^{b_0} Ca0b0 和 C a 1 b 1 . . . C a k b k C_{a_1}^{b_1}...C_{a_k}^{b_k} Ca1b1...Cakbk 两部分,首先对于 C a 0 b 0 C_{a_0}^{b_0} Ca0b0,它就等于 C a m o d p b m o d p C_{a \mod p}^{b \mod p} Camodpbmodp,因为我们将 a a a 和 b b b 写成 p p p 进制表示时,最后的余数就是 a 0 a_0 a0 和 b 0 b_0 b0 。接着,我们只需要证明一下 C a 1 b 1 . . . C a k b k = C a / p b / p C_{a_1}^{b_1}...C_{a_k}^{b_k} = C_{a / p}^{b / p} Ca1b1...Cakbk=Ca/pb/p 即可。
由于我们是先将 a a a 和 b b b,分别写成了 p p p 进制表示,
- a = a k p k + a k − 1 p k − 1 + . . . + a 1 p + a 0 a = a_kp^k+a_{k-1}p^{k-1} + ... + a_1p+a_0 a=akpk+ak−1pk−1+...+a1p+a0
- b = b k p k + b k − 1 p k − 1 + . . . + b 1 p + b 0 b = b_kp^k+b_{k-1}p^{k-1}+...+b_1p+b_0 b=bkpk+bk−1pk−1+...+b1p+b0
随后推出的 C a b ≡ C a 0 b 0 C a 1 b 1 . . . C a k b k m o d p C_a^b \equiv C_{a_0}^{b_0}C_{a_1}^{b_1}...C_{a_k}^{b_k} \mod p Cab≡Ca0b0Ca1b1...Cakbkmodp
现在,我们将 p p p 进制下的 a a a 和 b b b 分别右移一位(相当于除以 p p p),得到的是
- ⌊ a p ⌋ = a k p k − 1 + a k − 1 p k − 2 + . . . + a 1 \lfloor\frac{a}{p}\rfloor = a_kp^{k-1}+a_{k-1}p^{k-2} + ... + a_1 ⌊pa⌋=akpk−1+ak−1pk−2+...+a1
- ⌊ b p ⌋ = b k p k − 1 + b k − 1 p k − 2 + . . . + b 1 \lfloor\frac{b}{p}\rfloor = b_kp^{k-1}+b_{k-1}p^{k-2}+...+b_1 ⌊pb⌋=bkpk−1+bk−1pk−2+...+b1
我们只要将 ⌊ a p ⌋ \lfloor\frac{a}{p}\rfloor ⌊pa⌋ 和 ⌊ b p ⌋ \lfloor\frac{b}{p}\rfloor ⌊pb⌋ 带入前面的公式,就能得到如下式子(下面用 a / p a/p a/p 替代 ⌊ a p ⌋ \lfloor\frac{a}{p}\rfloor ⌊pa⌋, b / p b/p b/p 同理 )
- C a / p b / p = C a 1 b 1 C a 2 b 2 . . . C a k b k C_{a/p}^{b/p} = C_{a_1}^{b_1}C_{a_2}^{b_2}...C_{a_k}^{b_k} Ca/pb/p=Ca1b1Ca2b2...Cakbk
于是,整个卢卡斯定理得证,对于非负整数 a a a , b b b 以及质数 p p p ,有如下等式成立
C a b ≡ C a 0 b 0 ⋅ C a 1 b 1 ⋅ . . . ⋅ C a k b k ≡ C a m o d p b m o d p ⋅ C a / p b / p ( m o d p ) C_a^b \equiv C_{a_0}^{b_0} \cdot C_{a_1}^{b_1} \cdot ... \cdot C_{a_k}^{b_k} \equiv C_{a \mod p}^{b \mod p} \cdot C_{a / p}^{b / p} \space \space (\mod p) Cab≡Ca0b0⋅Ca1b1⋅...⋅Cakbk≡Camodpbmodp⋅Ca/pb/p (modp)
-
练习题:求组合数III
数据范围:1 <= n <= 20, 1 <= b <= a <= 10^18,1 <= p <= 10^5,其中 p 是质数
由于每组数据中 p 都不一样,所以这道题用预处理阶乘的方式不是特别合适,因为一次预处理的结果,只能适用于一组数据,对于下一组数据,由于 p 不同,还得重新计算一次阶乘。
// 1283ms
#include <iostream>
typedef long long LL;
using namespace std;
// 快速幂
LL qmi(LL a, LL b, LL p) {
LL res = 1;
while (b) {
if (b & 1) res = res * a % p;
a = a * a % p;
b >>= 1;
}
return res;
}
// 小于p的组合数直接求
LL C(LL a, LL b, LL p) {
if (b > a) return 0;
LL res = 1;
for (int i = a, j = 1; j <= b; j++, i--) {
res = res * i % p;
res = res * qmi(j, p - 2, p) % p;
}
return res;
}
// 卢卡斯定理
LL lucas(LL a, LL b, LL p) {
if (a < p && b < p) return C(a, b, p);
return C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}
int main() {
std::ios::sync_with_stdio(false);
LL n, a, b, p;
cin >> n;
while (n--) {
cin >> a >> b >> p;
printf("%lld\n", lucas(a, b, p));
}
return 0;
}
将上面的C函数修改一下,只在最后,算一次乘法逆元,可以极大的优化时间复杂度
LL C(LL a, LL b, LL p) {
if (b > a) return 0;
if (b > a - b) b = a - b;
LL x = 1, y = 1;
for (int i = a, j = 1; j <= b; j++, i--) {
x = x * i % p;
y = y * j % p;
}
return x * qmi(y, p - 2, p) % p;
}
完整代码如下
// 66ms
#include <iostream>
typedef long long LL;
using namespace std;
LL qmi(LL a, LL b, LL p) {
LL res = 1;
while (b) {
if (b & 1) res = res * a % p;
a = a * a % p;
b >>= 1;
}
return res;
}
LL C(LL a, LL b, LL p) {
if (b > a) return 0;
if (b > a - b) b = a - b; //小优化, 因为 C(a, b) = C(a, a - b)
LL x = 1, y = 1;
for (int i = a, j = 1; j <= b; j++, i--) {
x = x * i % p;
y = y * j % p;
}
// 只在最后求一次乘法逆元
return x * qmi(y, p - 2, p) % p;
}
LL lucas(LL a, LL b, LL p) {
if (a < p && b < p) return C(a, b, p);
return C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}
int main() {
std::ios::sync_with_stdio(false);
LL n, a, b, p;
cin >> n;
while (n--) {
cin >> a >> b >> p;
printf("%lld\n", lucas(a, b, p));
}
return 0;
}
至于时间复杂度,因为每次递归都是除以了个 p ,递归的层数就是
log
p
a
\log_pa
logpa,每层中的复杂度就是计算 C(a % p, b % p) 的复杂度,如果是优化之前,计算 C(a, b)最多需要算 b 次乘法,每次还需要求解个逆元,复杂度应该是
b
⋅
log
2
p
b \cdot \log_2p
b⋅log2p,优化后,只需要在最后求解一次逆元,复杂度是
b
+
log
2
p
b + \log_2p
b+log2p ,我们将
b
b
b 看成最大能取到
a
a
a,而
a
a
a 实际最大只能取到
p
−
1
p - 1
p−1,那么,优化前的复杂度是
O
(
log
p
N
⋅
p
⋅
log
2
p
)
O(\log_pN \cdot p \cdot \log_2p)
O(logpN⋅p⋅log2p),优化后的复杂度是
O
(
log
p
N
⋅
(
p
+
l
o
g
2
p
)
)
O(\log_pN \cdot (p + log_2p))
O(logpN⋅(p+log2p)) ,实际上由于在 b > a - b时,做了 b = a - b的优化,所以b实际最多取到 a / 2,优化后实际的复杂度会更低,实际只需要
log
p
N
⋅
(
p
2
+
log
2
p
)
\log_pN \cdot (\frac{p}{2} + \log_2p)
logpN⋅(2p+log2p),其中的
N
N
N 表示
a
a
a 的取值,这道题目的数据范围,
N
N
N 最大能取到
1
0
18
10^{18}
1018
卢卡斯定理,适用于 a 和 b 特别大,但是模数 p 是质数并且比较小的情况。
当 a 大于 p 时,不能依靠乘法逆元来进行计算,一是因为时间复杂度很高,二是因为 a 大于 p 时,[1, a]中间的一些数的乘法逆元不一定存在,因为某个数 x 在模 p 下的乘法逆元存在,一定要求 x 与 p 互质。
故需要使用卢卡斯定理。
高精度
前面几种求解组合数,都是求解在模某个数下的结果,而现在需要精确的求解出组合数的结果,这个结果可能很大。
求组合数IV
数据范围:1 <= b <= a <= 5000
思路:高精度,直接从公式出发。
C a b = a × ( a − 1 ) × ( a − 2 ) × . . . × ( a − b + 1 ) b × ( b − 1 ) × . . . × 1 = a ! b ! × ( a − b ) ! C_a^b = \frac{a × (a - 1) × (a - 2) × ... × (a - b + 1)}{b × (b - 1) × ... × 1} = \frac{a!}{b! × (a - b)!} Cab=b×(b−1)×...×1a×(a−1)×(a−2)×...×(a−b+1)=b!×(a−b)!a!
可以实现一个高精度乘法,以及一个高精度除法。但是那样的计算效率比较低,也比较难以实现。所以可以换一种思路,先对 C a b C_a^b Cab 分解一下质因数,然后只需要实现一个高精度乘法即可。
问题变成了,如何对 C a b C_a^b Cab分解质因数呢?可以先对分子中的 a ! a! a! 分解一下质因数,看某个因子出现了多少次,再对分母中的 b ! b! b! 和 ( a − b ) ! (a - b)! (a−b)! 分解一下质因数,把对应的因子的次数减掉。
但是如果对分子分母中每个数依次分解质因数,那么时间复杂度是 O ( N ⋅ N ) O(N \cdot \sqrt{N}) O(N⋅N),这道题目的数据范围是 5000,这个复杂度下也是不会超时的,但效率较低(之后自己试了下,效率相差也没有很大),可以换另一种方法,我们可以先把 5000 以内的质数全部预处理出来。
然后对于如何求解 a ! a! a! 的某个质因子 p p p 的次数,可以用这个公式进行计算
⌊ a p ⌋ + ⌊ a p 2 ⌋ + ⌊ a p 3 ⌋ + . . . + . . . \lfloor\frac{a}{p}\rfloor + \lfloor\frac{a}{p^2}\rfloor + \lfloor\frac{a}{p^3}\rfloor + ... + ... ⌊pa⌋+⌊p2a⌋+⌊p3a⌋+...+...
第一项是所有小于 a a a 的数中, p p p 的倍数的个数;但有的数可能是 p 2 p^2 p2 的倍数,但第一项只加了一次;所以我们需要再加上第二项 ,同理需要加上第三项,…,假设某个数分解质因数后,包含了 p k p^k pk ,那么该数对 p p p 的次数的贡献一共是 k k k,该数会被恰好加 k k k 次,在 ⌊ a p ⌋ \lfloor\frac{a}{p}\rfloor ⌊pa⌋ 时加1次,在 ⌊ a p 2 ⌋ \lfloor\frac{a}{p^2}\rfloor ⌊p2a⌋ 时加1次,…,在 ⌊ a p k ⌋ \lfloor\frac{a}{p^k}\rfloor ⌊pka⌋ 时加1次
所以我们的求解步骤是:
- 先用筛法求出
1-5000内的全部质数 - 对于分子和分母的阶乘表示,求出每个质数的次数
- 用高精度乘法将每个质因子乘起来
// 47ms
#include <iostream>
#include <vector>
using namespace std;
const int N = 5010;
int primes[N], cnt;
bool st[N];
int sum[N]; // 某个质数出现的次数
void get_primes(int n) {
for (int i = 2; i <= n; i++) {
if (!st[i]) primes[cnt++] = i;
for (int j = 0; primes[j] <= n / i; j++) {
st[primes[j] * i] = true;
if (i % primes[j] == 0) break;
}
}
}
// n! 中 , p 的次数为多少
int get(int n, int p) {
int res = 0;
while (n) {
res += n / p;
n /= p;
}
return res;
}
// 高精度乘法
vector<int> mul(vector<int> a, int b) {
int c = 0;
vector<int> res;
for (int i = 0; i < a.size(); i++) {
c += a[i] * b;
res.push_back(c % 10);
c /= 10;
}
while (c) {
res.push_back(c % 10);
c /= 10;
}
return res;
}
int main() {
std::ios::sync_with_stdio(false);
int a, b;
cin >> a >> b;
get_primes(a);
for (int i = 0; i < cnt; i++) {
int p = primes[i];
sum[i] = get(a, p) - get(b, p) - get(a - b, p);
}
vector<int> res;
res.push_back(1);
for (int i = 0; i < cnt; i++) {
for (int j = 0; j < sum[i]; j++) {
res = mul(res, primes[i]);
}
}
for (int i = res.size() - 1; i >= 0; i--) {
printf("%d", res[i]);
}
printf("\n");
return 0;
}
分别对每个数分解质因数,并计算次数,发现效率也没有相差的特别大
// 53ms
#include <iostream>
#include <vector>
#include <unordered_map>
using namespace std;
void process(int x, unordered_map<int, int>& m, bool add) {
for (int i = 2; i <= x / i; i++) {
while (x % i == 0) {
if (add) m[i]++;
else m[i]--;
x /= i;
}
}
if (x > 1) {
if (add) m[x]++;
else m[x]--;
}
}
vector<int> mul(vector<int> a, int b) {
vector<int> res;
int c = 0;
for (int i = 0; i < a.size(); i++) {
c += a[i] * b;
res.push_back(c % 10);
c /= 10;
}
while (c) {
res.push_back(c % 10);
c /= 10;
}
return res;
}
int main() {
std::ios::sync_with_stdio(false);
int a, b;
cin >> a >> b;
unordered_map<int, int> primes;
for (int i = a, j = 1; j <= b; j++, i--) {
process(i, primes, true);
process(j, primes, false);
}
vector<int> res;
res.push_back(1);
for (auto& [k, v] : primes) {
for (int i = 0; i < v; i++) {
res = mul(res, k);
}
}
for (int i = res.size() - 1; i >= 0; i--) {
printf("%d", res[i]);
}
printf("\n");
return 0;
}
卡特兰数
卡特兰数的应用非常广,很多方案的方案数都是卡特兰数。
比如火车进出栈问题(在某个操作序列的任意前缀中,进栈操作次数一定得大于等于出栈操作次数),合法括号序列(任意前缀中,左括号数量一定得大于等于右括号数量)。
应用题:889. 满足条件的01序列
给定 n 个 0 和 n 个 1,它们按照某种顺序排成长度为 2n 的序列,求满足任意前缀中0的个数都不小于1的个数的序列,有多少个。
我们可以先把问题进行一下转化
把任何一个排列转化成一个路径(比如一共6个1和6个0,0表示向右走,1表示向上走,那么每个排列,都可以表示为一条从坐标[0,0]走到[6,6]的路径)
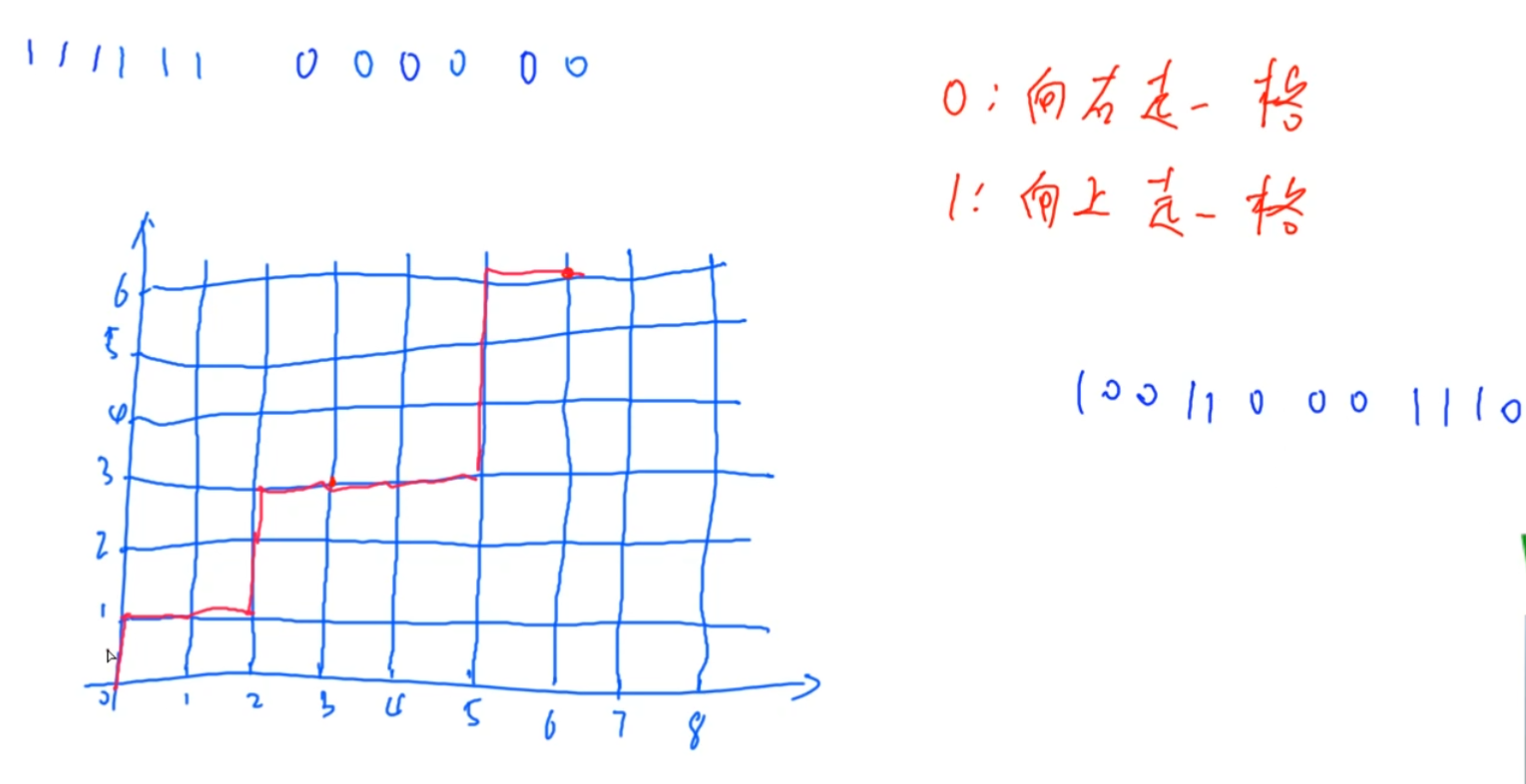
如果某个排列中,任意前缀中0的个数要大于等于1的个数,也就等价于,这个排列对应的路径,路径上的任何点的坐标(x, y),都要满足x >= y,于是我们可以画一条对角线 y = x,那么只要保证,路径始终位于这条对角线的下方(可以恰好到达对角线,但不能穿过这条对角线)。根据下图,也就等价于,在任何时刻,路径都必须在红色这条线的下方(严格的下方,不能到达红色这根线)
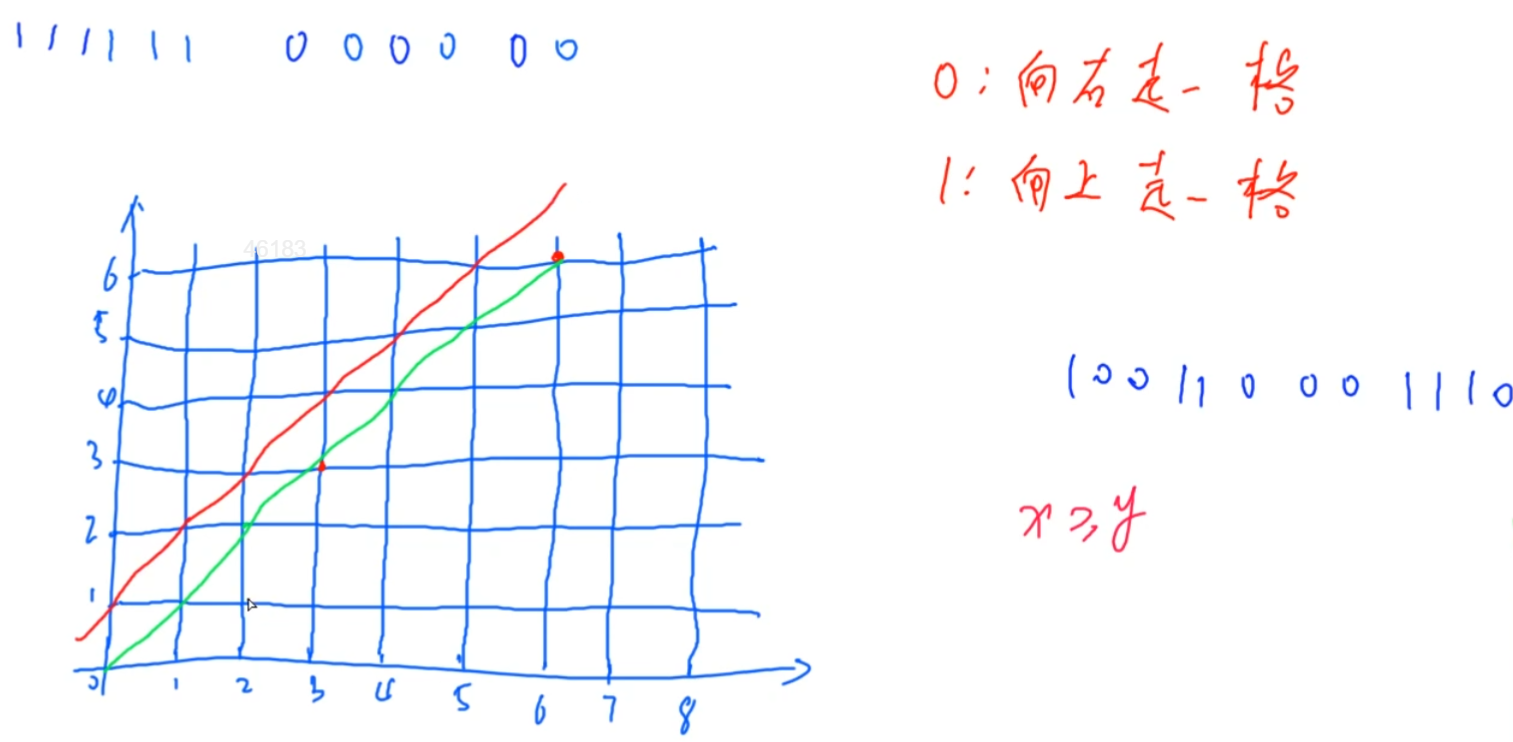
那么,现在问题等价于,求解所有从[0, 0]走到[6, 6],且不经过红色这条线的,所有路径的个数。
那么我们可以先求解所有路径的总数,然后再求解一下经过红色这条线的路径的个数,将两者相减,即得到答案。
对于上述 n = 6,总的路径数量就是 C 12 6 C_{12}^{6} C126 ,就是一共需要走12步,其中需要挑6步往上走。
那么经过红色这条线的路径的个数要怎么求呢?
对于任意一条经过红色这条线的路径,我们可以找到该路径与红线的第一个交点,然后把该点之后的剩余路径部分,关于红线做一个轴对称。
比如下面的橙线为一条经过红线的路径,我们将其与红线第一个交点之后的路径部分,关于红线做轴对称(加粗绿线),会发现其最终到达 [5, 7]这个点,这个点恰好和 [6, 6] 关于红线对称。
那么,任何一条经过红线的路径,我们都可以通过上述变换,将其转变为一条从[0, 0],走到[5, 7]的路径。所以,任何一条经过红线,从[0, 0]走到[6, 6]的路径,都能对应一条从[0, 0]走到[5, 7]的路径,反之同样成立。所以这两者是一一对应的,是可以等价的。
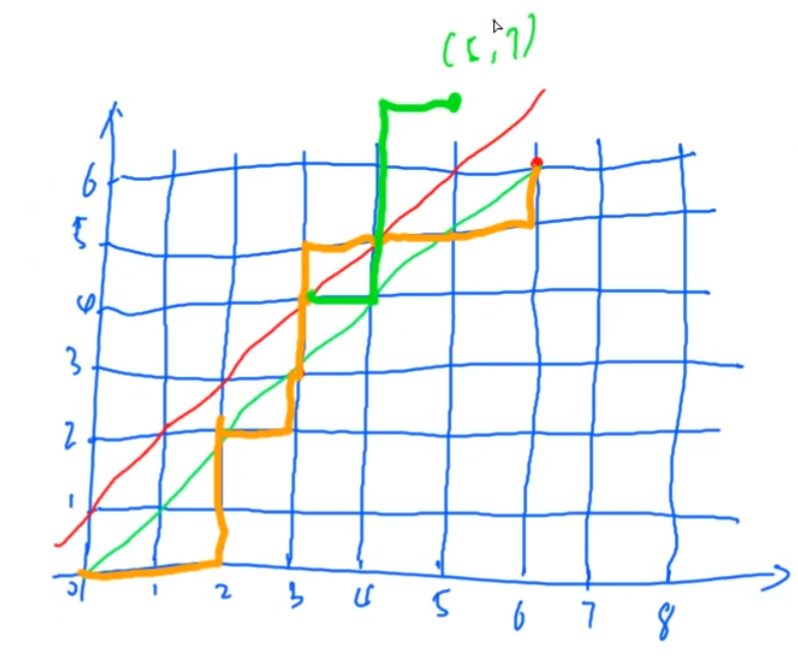
所以,经过红线从[0, 0] 走到[6, 6]的路径的个数,就等于从[0, 0] 走到 [5, 7] 的路径个数,而后者的个数计算很简单,就是
C
12
5
C_{12}^5
C125,所以对于 n = 6,问题的答案就是
C
12
6
−
C
12
5
C_{12}^6 - C_{12}^5
C126−C125
对于一般的 n,问题的答案则是: C 2 n n − C 2 n n − 1 = C 2 n n n + 1 C_{2n}^n - C_{2n}^{n-1} = \frac{C_{2n}^{n}}{n + 1} C2nn−C2nn−1=n+1C2nn
而这个数就被称为卡特兰数
// 295ms
#include <iostream>
typedef long long LL;
using namespace std;
const int MOD = 1e9 + 7;
int qmi(int a, int b, int p) {
int res = 1;
while (b) {
if (b & 1) res = (LL) res * a % p;
a = (LL)a * a % p;
b >>= 1;
}
return res;
}
int main() {
std::ios::sync_with_stdio(false);
int n;
cin >> n;
int res = 1;
for (int i = 2 * n, j = 1; j <= n; j++, i--) {
res = (LL)res * i % MOD;
res = (LL)res * qmi(j, MOD - 2, MOD) % MOD;
}
res = (LL)res * qmi(n + 1, MOD - 2, MOD) % MOD;
printf("%d\n", res);
return 0;
}
优化:
// 20ms
#include <iostream>
typedef long long LL;
using namespace std;
const int MOD = 1e9 + 7;
int qmi(int a, int b, int p) {
int res = 1;
while (b) {
if (b & 1) res = (LL) res * a % p;
a = (LL)a * a % p;
b >>= 1;
}
return res;
}
int main() {
std::ios::sync_with_stdio(false);
int n;
cin >> n;
int x = 1, y = n + 1;
for (int i = 2 * n, j = 1; j <= n; j++, i--) {
x = (LL)x * i % MOD;
y = (LL)y * j % MOD;
}
int res = (LL)x * qmi(y, MOD - 2, MOD) % MOD;
printf("%d\n", res);
return 0;
}