1. 前言

2. 数学原理

3. 代码实现

3.1 游戏设定

3.2 class State

3.3 class Action

3.4 Class Agent

3.5 Class Environment

4. 仿真结果及其分析

4.1 play()

4.2 value_evaluation_all_states(grid, max_steps)

4.3 value_evaluation_one_state(grid, s)

4.4 仿真结果及分析

1. 前言

在强化学习中，根据是否依赖于模型，可以分为基于模型（model-based）的强化学习和无模型（model-free）的强化学习。根据策略的更新和学习方法，强化学习算法可以分为基于价值函数的学习方法和基于策略的学习方法。

在基于价值函数的学习方法中，根据状态值函数（state-value function）的估计值，进行行动决策。比如说，从t时刻的状态 $s_t$ 出发，有K种行动可以选择：{ $a_1,a_2,...,a_K$ }，在各行动分别迁移到状态{ $s_{t+1}^1,s_{t+1}^2,...s_{t+1}^K$ }。那选择哪个动作呢？根据{ $s_{t+1}^1,s_{t+1}^2,...s_{t+1}^K$ }的值函数估计取其中的最大值并据此选择动作，即：

$k = \arg\max\limits_{i} V(s_{t+1}^i)$

这里的关键在于状态值函数的估计。在基于模型（model-based）的方法中，如果已知迁移函数 $T(s'|s,a)$ (T represent transit or transfer)和奖励函数 $R(s,s')$ （两者可以合并为Pr(s',r|s,a)）的话，可以基于动态规划的方法进行状态值函数的求解。对状态值函数的精确求解有比较严格的条件限制，更有实际应用意义的是对值函数进行近似求解，也称价值近似（value approximation）。价值近似可以通过价值迭代（value iteration）的方式进行。

本文（以及接下来的文章）描述价值估计或者近似的原理和实现。

2. 数学原理

根据前面的讨论我们知道在策略 $\pi(a|s)$ 的条件下，状态值函数的贝尔曼方程如下所示（参见：强化学习笔记：策略、值函数及贝尔曼方程）：

$\begin{align}v_\pi(s) &\doteq \mathbb{E}_\pi[G_t|S_t=s] \\&= \mathbb{E}_\pi[R_{t+1}+ \gamma G_{t+1}|S_t=s] \\&= \sum\limits_{a}\pi(a|s)\sum\limits_{s'}\sum\limits_{r}p(s',r|s,a)\big[r+\gamma\mathbb{E}_\pi[G_{t+1}|S_{t+1}=s'] \big] \\&= \sum\limits_{a\in \mathcal{A}}\pi(a|s)\sum\limits_{s'\in \mathcal{S},r\in \mathcal{R}}p(s',r|s,a)\big[r+\gamma v_\pi(s') \big] \ \forall s\in\mathcal{S} \quad\cdots(6,3.14) \end{align}$

假定即时奖励仅与迁移前后的状态有关，与所选择的动作无关，给定迁移函数 $T(s'|s,a)$ 和奖励函数 $R(s,s')$ ，则上式可以简化为：

$V_{\pi}(s)=\sum\limits_{a}\pi(a|s)\sum\limits_{s'}T(s'|s,a)[R(s,s')+\gamma V_\pi(s')]$ (1)

在基于策略的强化学习方法中，需要计算以上基于策略的价值函数（或状态值函数，state-value function）。但是在基于价值的学习方法中，价值函数可以简化如下：

$V(s)=\max\limits_{a}\sum\limits_{s'}T(s'|s,a)[R(s,s')+\gamma V_(s')]$ (2)

进一步，如果奖励只依赖于迁移后的状态，而与迁移前的状态无关的话，价值函数可以进一步简化为：

$V(s)=R(s) + \gamma \max\limits_{a}\sum\limits_{s'}T(s'|s,a) V(s')$ (3)

3. 代码实现

以下以一个满足奖励只依赖于迁移后状态，而与迁移前状态以及动作无关的简单的情况，给出以上公式（3）的实现实例。该实例相当于【2】中第1章和第2章的两个例子的结合，代码也是以【2】附书代码为基础改造而来。

3.1 游戏设定

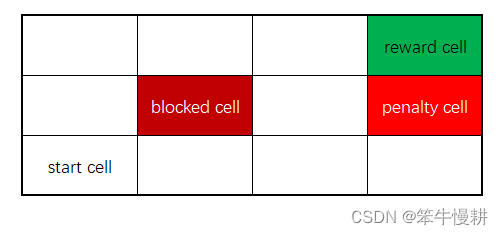
游戏在如下图所示3x4的迷你迷宫中进行。游戏规则如下：

从“start cell”出发，每一步agent可以选择上、下、左、右方向移动一格。“blocked cell”不能进入。到达"reward cell"获得1分奖励并结束游戏，到达"penalty cell"罚1分（或者说得到-1分的奖励）并结束游戏。

agent选择任何一个移动方向时，有move_prob的概率会沿着这个方向移动，有各(1-move_prob)/2的概率向两侧移动，不会沿反方向移动。

agent采取了上述行动后，如果是进入到“blocked cell”或者移动到迷宫以外了，都退回原位置（相当于浪费了一次动作）。

以下针对一些关键代码进行说明。

3.2 class State

State用于表示agent在迷宫中的2维坐标。以左上角为（0,0），右下角为（2,3），余者依此类推。

class State():

    def __init__(self, row=-1, column=-1):
        self.row = row
        self.column = column

    def __repr__(self):
        return "<State: [{}, {}]>".format(self.row, self.column)

    def clone(self):
        return State(self.row, self.column)

    def __hash__(self):
        return hash((self.row, self.column))

    def __eq__(self, other):
        return self.row == other.row and self.column == other.column

3.3 class Action

用Enum类型的类来表示可能的动作集合，如下所示：

class Action(Enum):
    UP = 1
    DOWN = -1
    LEFT = 2
    RIGHT = -2

3.4 Class Agent

class Agent():

    def __init__(self, env, max_recursion_depth):
        self.env     = env
        self.actions = env.actions
        self.max_recursion_depth = max_recursion_depth

    def policy(self, state):
        return random.choice(self.actions)

    def V(self, s, layer, gamma=0.99):
        # print('V(): s = [{0},{1}], layer={2}'.format(s.row,s.column,layer))
        reward, done = self.env.reward_func(s)
        value = reward + gamma * self.max_V_on_next_state(s,layer)
        return value

    def max_V_on_next_state(self, s, layer):
    # If game end, the future expected return(value) is 0. 
        # print('max_V_on_next_state(): s = [{0},{1}], layer={2}'.format(s.row,s.column,layer))        
        
        attribute = self.env.grid[s.row][s.column]
        if attribute == 1 or attribute == -1: 
            # print('Reach the end!')
            return 0
        if layer == self.max_recursion_depth:
            # print('Reach the recursion depth limit!')
            return -0.8

        values = []
        for a in self.actions:
            transition_probs = self.env.transit_func(s, a)
            v = 0
            for next_state in transition_probs:
                prob = transition_probs[next_state]
                v += prob * self.V(next_state,layer+1)
            values.append(v)
        return max(values)

Agent.policy()实现了一个纯粹随机的策略，这个对于基于价值的方法中的价值估计是没有影响的。因为基于价值的方法中的价值估计不依赖于策略。

V()和max_V_on_next_state()以相互递归调用的方式实现了第2章所述的公式（3）（代码与公式几乎是一一对应的）。值得注意的一点是，由于在本迷宫问题中，采取的是纯随机策略，agent在任何位置都是可上下左右四个方向任意运动，因此概率上是存在永远到达不了reward cell或penalty的情况的。这样的情况会导致以上递归调用无限进行下去最终导致内存崩溃。为了防止出现这种问题，实现中追加了每一局游戏中最大步数的限制，对应着递归调用中的递归深度。到达了最大步数但是仍然为到达终点的话，也给与-0.8的惩罚（不过，这个似乎应该体现在即时奖励那一块。一时没有想好应该怎么改，先这么着凑合了，等想明白了再来修改）。

3.5 Class Environment

Class Environment中几个关键方法的解释：

_move(self, state, action)-->next_state用于求在某一状态下经过指定action所到达的下一个状态。其中考虑如果越界或者进入了“blocked”会退回原地的处理。

transit_func(self, state, action)--> transition_probs: 用于构建状态迁移概率，即上文所述的迁移函数 $T(s'|s,a)$ 。

reward_func(self, state)-->reward, done: 计算 $R(s)$ 。如前所示，本游戏设定中，reward只依赖于（转移后）状态，所以可以非常简单地实现。

step(self, action)-->next_state, reward, done: 执行一步，其中调用了transit()方法。注意，它跟_move()的区别。_move()只是求某个状态在执行某个动作后到达的下一个状态，实际上并没有执行动作。而本方法是实际上在当前状态下执行指定动作并遵循环境模型的转移概率进行状态的更新。

class Environment():

    def __init__(self, grid, move_prob=0.8):
        # grid is 2d-array. Its values are treated as an attribute.
        # Kinds of attribute is following.
        #  0: ordinary cell
        #  -1: penalty cell (game end)
        #  1: reward cell (game end)
        #  9: block cell (can't locate agent)
        self.grid = grid
        self.agent_state = State()

        # Default reward is minus. Just like a poison swamp.
        # It means the agent has to reach the goal fast!
        self.default_reward = -0.04

        # Agent can move to a selected direction in move_prob.
        # It means the agent will move different direction
        # in (1 - move_prob).
        self.move_prob = move_prob
        self.reset()

    @property
    def row_length(self):
        return len(self.grid)

    @property
    def column_length(self):
        return len(self.grid[0])

    @property
    def actions(self):
        return [Action.UP, Action.DOWN,
                Action.LEFT, Action.RIGHT]

    @property
    def states(self):
        states = []
        for row in range(self.row_length):
            for column in range(self.column_length):
                # Block cells are not included to the state.
                if self.grid[row][column] != 9:
                    states.append(State(row, column))
        return states

    def transit_func(self, state, action):
        transition_probs = {}
        if not self.can_action_at(state):
            # Already on the terminal cell.
            return transition_probs

        opposite_direction = Action(action.value * -1)

        for a in self.actions:
            prob = 0
            if a == action:
                prob = self.move_prob
            elif a != opposite_direction:
                prob = (1 - self.move_prob) / 2

            next_state = self._move(state, a)
            if next_state not in transition_probs:
                transition_probs[next_state] = prob
            else:
                transition_probs[next_state] += prob

        return transition_probs

    def can_action_at(self, state):
        if self.grid[state.row][state.column] == 0:
            return True
        else:
            return False

    def _move(self, state, action):
        if not self.can_action_at(state):
            raise Exception("Can't move from here!")

        next_state = state.clone()

        # Execute an action (move).
        if action == Action.UP:
            next_state.row -= 1
        elif action == Action.DOWN:
            next_state.row += 1
        elif action == Action.LEFT:
            next_state.column -= 1
        elif action == Action.RIGHT:
            next_state.column += 1

        # Check whether a state is out of the grid.
        if not (0 <= next_state.row < self.row_length):
            next_state = state
        if not (0 <= next_state.column < self.column_length):
            next_state = state

        # Check whether the agent bumped a block cell.
        if self.grid[next_state.row][next_state.column] == 9:
            next_state = state

        return next_state

    def reward_func(self, state):
        reward = self.default_reward
        done = False

        # Check an attribute of next state.
        attribute = self.grid[state.row][state.column]
        if attribute == 1:
            # Get reward! and the game ends.
            reward = 1
            done = True
        elif attribute == -1:
            # Get penalty! and the game ends.
            reward = -1
            done = True
        elif attribute == 9:
            # Cannot enter this cell. Add this branch here just for the completeness of state-value estimation.
            reward = 0
            done = True
            
        return reward, done

    def reset(self):
        # Locate the agent at lower left corner.
        self.agent_state = State(self.row_length - 1, 0)
        return self.agent_state

    def step(self, action):
        next_state, reward, done = self.transit(self.agent_state, action)
        if next_state is not None:
            self.agent_state = next_state

        return next_state, reward, done

    def transit(self, state, action):
        transition_probs = self.transit_func(state, action)
        if len(transition_probs) == 0:
            return None, None, True

        next_states = []
        probs = []
        for s in transition_probs:
            next_states.append(s)
            probs.append(transition_probs[s])

        next_state = np.random.choice(next_states, p=probs)
        reward, done = self.reward_func(next_state)
        return next_state, reward, done

4. 仿真结果及其分析

本文实现了以下几种utility function用于执行各种不同的仿真。

4.1 play()

def play(grid, num_episodes):
    env = Environment(grid)
    agent = Agent(env,5)

    # Try 10 games (one game is one episode).
    for i in range(num_episodes):
        # Initialize position of agent.
        state = env.reset()
        total_reward = 0
        done = False
    
        while not done:
            action = agent.policy(state)
            next_state, reward, done = env.step(action)
            total_reward += reward
            state = next_state
    
        print("Episode {}: Agent gets {:6.2f} reward.".format(i, total_reward))

单纯地在既定的随机策略条件下运行了若干次游戏，看看agent最终会得到多少奖励。这是一个单纯的关于随机策略条件下所能获得的奖励的蒙特卡洛仿真。可以指定一个较大的num_episodes，然后根据仿真结果进行所获得奖励的统计特性分布。这个不是本文的主题，就此略过。

4.2 value_evaluation_all_states(grid, max_steps)

基于前文所述公式(3)估计各个状态的状态值。需要注意的是，运行时间是随着最大步数（递归深度）呈指数级上升的，所以不能设的太大。

def value_evaluation_all_states(grid, max_steps):
    for k in range(max_steps):    
        print('================================================')        
        print('max_steps = {0}'.format(k))        
        env = Environment(grid)
        agent = Agent(env,k)
        
        t_start = time.time()
        for i in range(len(grid)):
            for j in range(len(grid[0])):            
                s = State(i,j)
                print('s = {0}, agent.V(s) = {1:6.3f}'.format(s, agent.V(s,0)))
        t_stop = time.time()
        print('time cost = {0:6.2f}(sec)'.format((t_stop-t_start)))
        print('')

4.3 value_evaluation_one_state(grid, s)

针对某一个状态，考察不同的最大步数（递归深度）限制会对状态值的估计有什么影响。

def value_evaluation_one_state(grid, s):
    for max_steps in range(8):    
        print('================================================')        
        print('max_steps = {0}'.format(max_steps))        
        env = Environment(grid)
        agent = Agent(env,max_steps)
        
        t_start = time.time()
        print('s = {0}, agent.V(s) = {1:6.3f}'.format(s, agent.V(s,0)))
        t_stop = time.time()
        print('time cost = {0:6.2f}(sec)'.format((t_stop-t_start)))
        print('')

4.4 仿真结果及分析

if __name__ == "__main__":

    # Creat grid environment
    grid = [
        [0, 0, 0, 1],
        [0, 9, 0, -1],
        [0, 0, 0, 0]
    ]
    
    
    play(grid, 10)
    
    value_evaluation_all_states(grid, 7)
    
    s = State(len(grid)-1,0) # Start from left-bottom cell
    value_evaluation_one_state(grid, s)

value_evaluation_one_state(grid, State[2,0])（即左下角start cell）在不同步数限制条件下的仿真结果如下所示：

================================================
max_steps = 0
s = <State: [2, 0]>, agent.V(s) = -0.832
time cost = 0.00(sec)

================================================
max_steps = 1
s = <State: [2, 0]>, agent.V(s) = -0.864
time cost = 0.00(sec)

================================================
max_steps = 2
s = <State: [2, 0]>, agent.V(s) = -0.895
time cost = 0.00(sec)

================================================
max_steps = 3
s = <State: [2, 0]>, agent.V(s) = -0.926
time cost = 0.01(sec)

================================================
max_steps = 4
s = <State: [2, 0]>, agent.V(s) = -0.957
time cost = 0.11(sec)

================================================
max_steps = 5
s = <State: [2, 0]>, agent.V(s) = -0.346
time cost = 1.38(sec)

================================================
max_steps = 6
s = <State: [2, 0]>, agent.V(s) = 0.066
time cost = 16.84(sec)

================================================
max_steps = 7
s = <State: [2, 0]>, agent.V(s) = 0.339
time cost = 197.92(sec)

首先，可以看出时间的确是随步数增长而呈急剧增大。 max_steps=8需要接近半个小时以上了。其次，由于从start cell出发至少需要5步才能到达“reward cell”，到达“penalty cell”最少需要“penalty cell”，所以仿真结果表明max_steps设为6以上价值函数才变为正数，基本上符合直觉。但是，如何判断这个结果是否正确呢？对于简单的情况可以通过手动计算，与程序运行结果进行对照确认。但是本问题这样的情况可能会显得过于繁琐。另外一种方法是用不同的方法实现看看不同方法所得到的结果会不会一致。这个，下一篇将考虑采用价值迭代（value iteration）的方式来近似计算本问题中的状态值，这样的话就可以进行对照了。敬请期待。。。

本文完整代码将上传github...wait a minute...

参考文献：

【1】Sutton, et, al, Introduction to reinforcement learning (2020)

【2】久保隆宏著，用Python动手学习强化学习