MATLAB | 儿童节一起来玩转MATLAB叭

news2024/11/20 21:35:11

hey, 儿童节要到啦，提前祝各位大朋友，小朋友儿童节快乐，本篇将会在前半部分给出一些有趣且简短的代码，在后半部分展示一下我准备的游戏大礼包里面的游戏效果，完整代码获取方式请见文末，让我们一起玩转MATLAB叭(请尽量使用R2018b及之后版本)：

有趣代码

该部分有一部分是我以前的代码进行的重写，有一部分是粉丝问我要的代码，还有一部分是对大佬代码的改写：

平面大钻石

% author : slandarer
figure('render','painters')
hold on; axis equal; axis([-30,30,-30,30])
CList = [21,97,169; 68,107,178; 169,217,246; 76,177,227; 92,134,195; 55,124,199]./255;
set(gca, 'XColor','none', 'YColor','none', 'Color',[0,64,115]./510)
t = 0:20:360-1;
T = [cosd(t).*7; sind(t).*7; t];
plot([1; 0]*T(1,:), [1; 0]*T(2,:), 'LineWidth',2)
for i = 1:5
    t = T(3,:);
    L = T + [cosd(t - 20)*(7 - i); sind(t - 20)*(7 - i); t*0 - 20];
    R = T + [cosd(t + 20)*(7 - i); sind(t + 20)*(7 - i); t*0 + 20];
    plot([T(1,:); L(1,:)], [T(2,:); L(2,:)], 'LineWidth',2)
    plot([T(1,:); R(1,:)], [T(2,:); R(2,:)], 'LineWidth',2)
    T = [L, R];
end
LHdl = findobj(gca, 'Type','line');
for i = 1:length(LHdl)
    LHdl(i).Color = CList(randi([1,6],[1,1]),:);
end
P = T(1:2,:).';
[k,~] = convhull(P);
plot(P(k,1), P(k,2), 'LineWidth',2, 'Color',CList(1,:))

羽毛

% author : slandarer
% remixed from Juan Villacrés / Flower R-D
figure('Color','k', 'Renderer','painters', 'InvertHardCopy', 'off')
hold on
t = linspace(-3, 3, 1000);
x = 7*sin(7.32*t)./(1 + cos(1.42*t).^2);
y = 7*cos(1.42*t).*sin(7.32*t).^4;
for i = 0:pi/3:2*pi
    m = [cos(i) -sin(i); sin(i) cos(i)]*([x; y]);
    patch([m(1,:), NaN], [m(2,:), NaN], - [sqrt(m(1,:).^2+m(2,:).^2), NaN],...
        'EdgeColor','interp', 'Marker','none', 'MarkerFaceColor','flat', 'LineWidth',1)
end
axis equal off
colormap(bone)

樱花树

一个用循环一个用的递归：

% author : slandarer
hold on; axis([-1,5,0,5])
set(gca, 'XColor','none', 'YColor','none', 'Color',[.5,.5,.5])
T=[1.2; 0; pi/2]; a = pi/10;
for i = 1:16
    L = .6*.9^i;
    I = randi(25, [1,size(T,2)]) > 9;
    if i == 1,I = ~1; end
    L1 = T(:,I); t = L1(3,:);
    R1 = L1 + [cos(t - a)*L; sin(t - a)*L; t*0 - a];
    R2 = L1 + [cos(t + a)*L; sin(t + a)*L; t*0 + a];
    L2 = T(:,~I); t = L2(3,:);
    R3 = L2 + [cos(t)*L; sin(t)*L; t*0];
    T = [R1, R2, R3];
    X = [L1(1,:), L1(1,:), L2(1,:); R1(1,:), R2(1,:), R3(1,:)]; X(end+1,:) = nan;
    Y = [L1(2,:), L1(2,:), L2(2,:); R1(2,:), R2(2,:), R3(2,:)]; Y(end+1,:) = nan;
    plot(X(:), Y(:), 'Color',[0 0 0] + i*.3/16, 'LineWidth',5*0.8^i)
    if i > 14
        scatter(T(1,:),T(2,:), i*2-20, 'CData',[.86,.68,.68]/(1 - .13*(i - 15)));
    end
end


% 原代码出自：Sebastian Kraemer
% 注释改编自：slandarer
hold on;
% 绘制背景
C = [123,159,190;228,214,200]./255;
CN = size(C,1);
CM = linspace(1,0,100).'*ones(1,100);
M(:,:,1) = interp1(linspace(0,1,CN),C(:,1),CM);
M(:,:,2) = interp1(linspace(0,1,CN),C(:,2),CM);
M(:,:,3) = interp1(linspace(0,1,CN),C(:,3),CM);
image([.5,14],[3.2,13],M)

E = F([0,1]);
% 绘制山
fill([-6,7,10,12,15,28],[.2,5.5,7.8,7.8,5.5,.2],[.2,5.5,7.8,7.8,5.5,.2], 'EdgeColor','none');
% 绘制树
fill(real(E),imag(E),2, 'EdgeColor','none');
scatter(real(E),imag(E),30,'CData',[1,.7,.7],'Marker','h','MarkerEdgeAlpha',.05);

colormap bone;
axis off;
axis([.5,14,0,13])

function V = F(p)
V = [];
if abs(diff(p)) > 8e-3
    % ^  C____D
    % | /\   /
    % |/  \ /
    % A----B
    % |    |
    % |    |
    % 0----1
    % 假设0，1节点为原节点，则乘虚数i是为了得到与01向量方向垂直的向量
    % 原始节点再加上该向量便得到A,B节点，
    % 后面的1i^cos(...)^.5是为了得到C,D节点
    % cos(...)的范围为[-1, 1], ^cos(...)是为了将1i旋转至[-pi, pi]范围，
    % 再^.5将其旋转范围调整至[-pi/2, pi/2]范围，-1i再在前面乘i*diff(p)
    % 就能接下来生成C,D，并且在向量的右半边方向
    % 这样就能看似随机，实则依靠norm(p)对左右两个树枝的宽度和角度进行调整  
    Z = p + .5i*diff(p)*[4; 4 - 1i + 1i^cos(283*norm(p))^.5];
    % 使用平行四边形的AC边和CB边作为原节点再进行递归，使树进行分叉
    V = [p(1); F(Z(1:2)); F(Z(2:3)); p(2)];     
end
end

毕达哥拉斯树

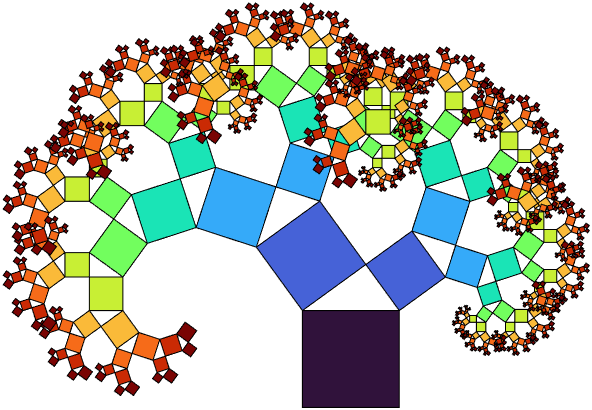
% author : slandarer
clc; clear
X = [0, 1, 1, 0];
Y = [0, 0, 1, 1];
MF = @(T) [cos(T), sin(T); -sin(T), cos(T)];
M1 = MF(pi/2); M2 = MF(-pi/2); M3 = MF(pi/2.5);
N = 10; CL = turbo(N);

ax = gca; 
ax.DataAspectRatio = [1,1,1];
ax.NextPlot = 'add';
ax.XColor = 'none';
ax.YColor = 'none';
fill(X,Y, CL(1,:))

for i = 2:N
    XM = X(:,3)./2 + X(:,4)./2; XV = X(:,3)./2 - X(:,4)./2;
    YM = Y(:,3)./2 + Y(:,4)./2; YV = Y(:,3)./2 - Y(:,4)./2;
    XYM = [XV, YV]*M3 + [XM, YM]; 
    XR = [XYM(:,1), X(:,3)]; XL = [X(:,4), XYM(:,1)];
    YR = [XYM(:,2), Y(:,3)]; YL = [Y(:,4), XYM(:,2)];
    XYR3 = [XR(:,1) - XR(:,2), YR(:,1) - YR(:,2)]*M2 + [XR(:,2), YR(:,2)];
    XYR4 = [XR(:,2) - XR(:,1), YR(:,2) - YR(:,1)]*M1 + [XR(:,1), YR(:,1)];
    XYL3 = [XL(:,1) - XL(:,2), YL(:,1) - YL(:,2)]*M2 + [XL(:,2), YL(:,2)];
    XYL4 = [XL(:,2) - XL(:,1), YL(:,2) - YL(:,1)]*M1 + [XL(:,1), YL(:,1)];
    X = [XR, XYR3(:,1), XYR4(:,1); XL, XYL3(:,1), XYL4(:,1)];
    Y = [YR, XYR3(:,2), XYR4(:,2); YL, XYL3(:,2), XYL4(:,2)];
    fill(X.',Y.', CL(i,:))
end


% author : slandarer
E = F([0,1], 13);
fill(real(E),imag(E),imag(E), 'EdgeColor','none');
hold on; axis equal off
colormap(cool)
function V = F(p, n)
T = 36;
V = [];
if n > 0
    Z = p + 1i*diff(p)*[1; 1 + cosd(T)*cosd(T-90) + cosd(T)*sind(T-90)*1i];
    V = [p(1); F(Z(1:2), n - 1); F(Z(2:3), n - 1); p(2)];
end
end

彩色涟漪

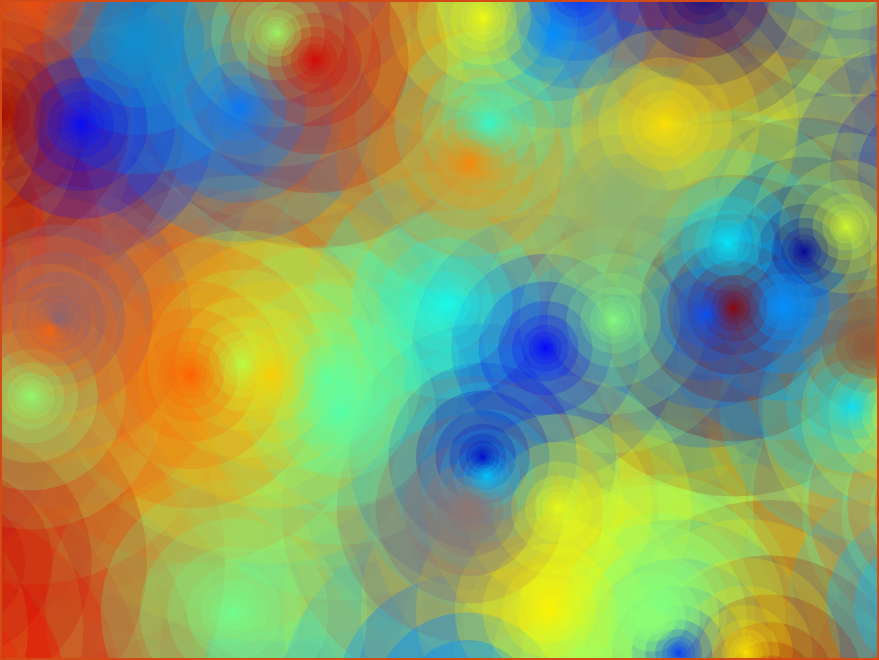
% author : slandarer
hold on; axis tight equal
XY = rand(200,2).*[2,1.2];
n = 100; s = 2^n;
r = randi(size(XY,1), n, 1);
for j = 1:n
    scatter(XY(r,1),XY(r,2), s/2^(j-1), jet(n), 'filled', 'MarkerFaceAlpha',.2);
end
camva(3)

随机油画

% author : slandarer
% 复刻自 : Martin Ender
clc; clear
r=@(n) randi([0,n-1], [1,1]);
P(:,:,1) = randMat();
P(:,:,2) = randMat();
P(:,:,3) = randMat();
imshow(uint8(P))
function M = randMat()
r = @(n) randi([0,n-1],[1,1]);
M = zeros(512,512);
for i = 1:512
    for j = 1:512
        M(i,j) = getC(i,j);
    end
end
    function C = getC(i,j)
        if M(i,j) == 0
            if r(99) ~= 0
                M(i,j) = getC(mod(i+r(2),512)+1,mod(j+r(2),512)+1);
            else
                M(i,j) = r(256);
            end
        end
        C = M(i,j);
    end
end

绿水青山

% 原代码出自：Tim
% 注释改编自：slandarer
clc; clear; close all;
a = 200;
X = (.5:a)'./a;
CL = (- cos(X.*2.*pi) + 1).^.2;
r = repmat((X - .5)'.^2, a, 1) + repmat((X - .5).^2, 1, a);
Z = abs(ifftn(exp(7i.*rand([a,a]))./r.^.9)).*(CL*CL').*30;
% 画山
surf(repmat(X, 1, a), repmat(X', a, 1), Z);
m = 50;
l = (m:-1:1)./m;
% 绘制云彩
hold on
for n = 1:m
    surf(repmat(X, 1, a), repmat(X', a, 1), ones([a,a]).*n, ones([a,a,3]), 'EdgeAlpha',0, 'FaceAlpha',max(.2, l(n))./2);
end
zlim([-a/2,a]);
shading flat;
CList = [140,116,78; 171,135,87; 187,170,101; 162,181,117; 95,175,146; 
         79,183,160; 72,162,163; 44,132,152; 36,116,141; 65,64,123; 40,26,44]./255;
CList = interp1(1:size(CList, 1), CList, linspace(1, size(CList, 1), 100));
colormap(CList);
camva(5);
axis off

星球

% 原代码出自：Tim
% 注释改编自：slandarer

% 先画一个bone渐变色的球
[a,b,c] = sphere(99);
surf(a,b,c);
colormap bone
hold on

% 在球面外生成一些随机点
% 进行三角剖分后
% 设置成半透明冷色
% 一些透明三角形交错叠加形成炫酷星球
x = randn(3,999);       
x = 1.01*x./vecnorm(x);
p = delaunay(x');
h = patch('faces',p, 'vertices',x', 'FaceVertexCData',pink(size(p,1)), 'FaceAlpha',.25);
% 设置坐标区域比例
axis equal off
% 设置背景色
set(gcf, 'color','k')
set(gcf, 'InvertHardCopy','off')
% 平滑星球表面配色
shading flat

% 在星球外生成一些随机点当作星星
r=@()rand(1,3e2);
scatter(r()*10-5, r()*10-5, r().^2*200, '.w');
camva(2)

画圈圈

% bird 1
K = 1:9830;
t = linspace(0,2*pi,200);

X = @(k) (sin(pi.*k./2e4)).^12.*(cos(31.*pi.*k./1e4).^16.*sin(6.*pi.*k./1e4)./2+sin(31.*pi.*k./1e4).^20./6)...
        +3.*k./2e4+cos(31.*pi.*k./1e4).^6.*sin(pi./2.*(k./1e4-1).^7-pi./5);
Y = @(k) -9./4.*cos(31.*pi.*k./1e4).^6.*cos(pi./2.*(k./1e4-1).^7-pi./5).*(2./3+(sin(pi.*k./2e4).*sin(3.*pi.*k./2e4)).^6)...
        +3./4.*cos(3.*pi.*(k-1e4)./1e5).^10.*cos(9.*pi.*(k-1e4)./1e5).^10.*cos(36.*pi.*(k-1e4)./1e5).^14+7./10.*((k-1e4)./1e4).^2;
R = @(k) sin(pi.*k./2e4).^10.*(1./4.*cos(31.*pi.*k./1e4+25.*pi./32).^20+1./20.*cos(31.*pi.*k./1e4).^2)+1./30.*(3./2-cos(62.*pi.*k./1e4).^2);

CX = [X(K') + cos(t).*R(K'), K'.*nan]';
CY = [Y(K') + sin(t).*R(K'), K'.*nan]';
plot(CX(:),CY(:), 'Color',[0,0,0,.2]);
set(gca, 'DataAspectRatio',[1,1,1], 'XColor','none', 'YColor','none');


% bird 2
K = -2e4:2e4;
t = linspace(0,2*pi,200);

X = @(k) k./15e3+sin(17.*pi./20.*(k./2e4).^5).*cos(41.*pi.*k./2e4).^6+...
        (1./3.*cos(41.*pi.*k./2e4).^16+1./3.*cos(41.*pi.*k./2e4).^80).*cos(pi.*k./4e4).^12.*sin(6.*pi.*k./2e4);
Y = @(k) 1./2.*(k./2e4).^4-cos(17.*pi./20.*(k./2e4).^5).*(11./10+45./20.*cos(pi.*k./4e4).^8.*cos(3.*pi.*k./4e4).^6).*cos(41.*pi.*k./2e4).^6+...
        12./20.*cos(3.*pi.*k./2e5).^10.*cos(9.*pi.*k./2e5).^10.*cos(8.*pi.*k./2e5).^10;
R = @(k) 1./50+1./40.*sin(41.*pi.*k./2e4).^2.*sin(9.*pi.*k./2e5).^2+1./17.*cos(41.*pi.*k./2e4).^2.*cos(pi.*k./4e4).^10;

CX = [X(K') + cos(t).*R(K'), K'.*nan]';
CY = [Y(K') + sin(t).*R(K'), K'.*nan]';
plot(CX(:),CY(:), 'Color',[0,0,0,.2]);
set(gca, 'DataAspectRatio',[1,1,1], 'XColor','none', 'YColor','none');


% butterfly 1
K = 1:4e4;
t = linspace(0, 2*pi, 200);

X = @(k) 3./2.*cos(141.*pi.*k./4e4).^9.*(1-1./2.*sin(pi.*k./4e4)).*(1-1./4.*cos(2.*pi.*k./4e4).^30.*(1+cos(32.*pi.*k./4e4).^20)).*...
        (1-1./2.*sin(2.*pi.*k./4e4).^30.*sin(6.*pi.*k./4e4).^10.*(1./2+1./2.*sin(18.*pi.*k./4e4).^20));
Y = @(k) cos(2.*pi.*k./4e4).*cos(141.*pi.*k./4e4).^2.*(1+1./4.*cos(pi.*k./4e4).^24.*cos(3.*pi.*k./4e4).^24.*cos(21.*pi.*k./4e4).^24);
R = @(k) 1./100+1./40.*(cos(141.*pi.*k./4e4).^14+sin(141.*pi.*k./4e4).^6).*(1-cos(pi.*k./4e4).^16.*cos(3.*pi.*k./4e4).^16.*cos(12.*pi.*k./4e4).^16);

CX = [X(K') + cos(t).*R(K'), K'.*nan]';
CY = [Y(K') + sin(t).*R(K'), K'.*nan]';
plot(CX(:),CY(:), 'Color',[0,0,0,.2]);
set(gca, 'DataAspectRatio',[1,1,1], 'XColor','none', 'YColor','none');


% butterfly 2
K = 1:4e4;
t = linspace(0, 2*pi, 200);

X = @(k) 6./5.*cos(141.*pi.*k./4e4).^9.*(1-1./2.*sin(pi.*k./4e4).^3).*(1-1./4.*cos(2.*pi.*k./4e4).^30.*(1+2./3.*cos(30.*pi.*k./4e4).^20)-...
        sin(2.*pi.*k./4e4).^10.*sin(6.*pi.*k./4e4).^10.*(1./5+4./5.*cos(24.*pi.*k./4e4).^20));
Y = @(k) cos(2.*pi.*k./4e4).*cos(141.*pi.*k./4e4).^2.*(1+1./4.*cos(pi.*k./4e4).^24.*cos(3.*pi.*k./4e4).^24.*cos(19.*pi.*k./4e4).^24);
R = @(k) 1./100+1./40.*(cos(2820.*pi.*k./4e4).^6+sin(141.*pi.*k./4e4).^2).*(1-cos(pi.*k./4e4).^16.*cos(3.*pi.*k./4e4).^16.*cos(12.*pi.*k./4e4).^16);

CX = [X(K') + cos(t).*R(K'), K'.*nan]';
CY = [Y(K') + sin(t).*R(K'), K'.*nan]';
plot(CX(:),CY(:), 'Color',[0,0,0,.2]);
set(gca, 'DataAspectRatio',[1,1,1], 'XColor','none', 'YColor','none');

柔线球

function Iris
% 灵感来自 Oliver Brotherhood 的 Processing 作品 Iris
% 由 slandarer 使用 MATLAB 进行复刻
% 生成连续随机角度
randList  = (rand(30,3) - .5).*2.*3.15;
thetaList = interp1(linspace(1, 3000, 30), randList, 1:3000, 'makima').';
% 渐变颜色
% #046380, #16193B, #35478C, #4E7AC7, #7FB2F0, #ADD5F7
CList = [4 99 128; 22 25 59; 53 71 140; 78 122 199; 127 178 240; 173 213 247]./255;
CList = interp1(linspace(1, 3000, size(CList, 1)), CList, 1:3000, 'linear');
% 坐标区域修饰
hold on; axis tight equal off
% 随机椭圆半径
A = rand(2,1); B = rand(2,1);
for i = 1:3000
    X = [0; A.*cos(thetaList([1,2],i)); cos(thetaList(3,i))];
    Y = [0; B.*sin(thetaList([1,2],i)); sin(thetaList(3,i))];
    coe2 = ((linspace(0, 1, 100)).^((0:3)')).*((1 - linspace(0, 1, 100)).^((3:-1:0)'));
    bezierPnts = ([1,3,3,1].*coe2.') * [X,Y];
    plot(bezierPnts(:,1),bezierPnts(:,2), 'Color',[CList(i,:), .2], 'LineWidth',.5)
    % pause(.01)
end
end

旋转多边形

% author : slandarer
% remixed from Daniel Pereira / Ghost Pentagon Flower
T = linspace(0, 360, 6).';
I = 20:-1:1;
fill(I.*sind(T + 18.*I), I.*cosd(T + 18.*I), I, 'edgecolor','none')
colormap(bone); axis equal off; set(gcf, 'color','w');

炫酷像素画

% @author:slandarer
[X,Y]=meshgrid(0:1023);
P(:,:,1)=bitand(bitand(mod(X,Y),mod(Y,X)),255);
P(:,:,2)=bitand(bitxor(mod(X,Y),mod(Y,X)),255);
P(:,:,3)=bitand(bitor(mod(X,Y),mod(Y,X)),255);
imshow(uint8(P))
% [X,Y]=meshgrid(0:1023);
% P(:,:,1)=mod(bitand(mod(X,Y),mod(Y,X)),255);
% P(:,:,2)=mod(bitxor(mod(X,Y),mod(Y,X)),255);
% P(:,:,3)=mod(bitor(mod(X,Y),mod(Y,X)),255);
% imshow(uint8(P))

水晶爱心

% author : slandarer
hold on; grid on
axis([-22,22, -20,20, -10,10])
axis off
s = pi/8; t = [0:.2:s, s:.02:pi-s, pi-s:.2:pi+s, pi+s:.02:2*pi-s, 2*pi-s:.2:2*pi];
x = 16*sin(t).^3;
y = 13*cos(t) - 5*cos(2*t) - 2*cos(3*t) - cos(4*t);
lW = 'LineWidth';
plot3(x,y,x.*0, 'Color',[186,110,64]./255, lW,1)
set(gca, 'DataAspectRatio',[1,1,1])
for i = 1:length(t)
    for j = 1:6
        L = rand(1)*2.5 + 1.5;
        A = rand(1,3) - .5;
        A = A./norm(A);
        B = [x(i), y(i), 0];
        C = [A(3), A(3), -A(1)-A(2)];
        P0 = [.8.*A.*L + B + C./norm(C).*.14.*L, 1]';
        a = B(1); b = B(2); c = 0; u = A(1); v = A(2); w = A(3);
        for k = 1:4
            o = k*pi/2; co = cos(o); so = sin(o); cn = 1 - co;
            RM = [u^2 + (v^2 + w^2)*co, u*v*cn - w*so, u*w*cn + v*so, (a*(v^2 + w^2) - u*(b*v + c*w))*cn + (b*w - c*v)*so;
                  u*v*cn + w*so, v^2 + (u^2 + w^2)*co, v*w*cn - u*so, (b*(u^2 + w^2) - v*(a*u + c*w))*cn + (c*u - a*w)*so;
                  u*w*cn - v*so, v*w*cn + u*so, w^2 + (u^2 + v^2)*co, (c*(u^2 + v^2) - w*(a*u + b*v))*cn + (a*v - b*u)*so];
            P(:,k) = RM*P0;
        end
        F = [1,3,4; 1,4,5; 1,5,6; 1,6,3; 2,3,4; 2,4,5; 2,5,6; 2,6,3];
        patch('Faces',F, 'Vertices',[B;B + A.*L; P'], 'FaceColor',[0,71,177]./255,...
            'FaceAlpha',.2, 'EdgeColor',[0,63,159]./255,...
            'EdgeAlpha',.25, lW,.01)
    end
end

山水画

% python出处：童晶|《Python趣味创意编程》
% MATLAB代码改写 ：slandarer
% 计算基础数据
a = 800; b = 600;
d = (.5:a)'/a;
s = (-cos(d*2*pi) + 1).^.2;
f = d-.5; r = f'.^2 + f.^2;
% 坐标区域修饰
hold on
axis([0,a,0,b]);
set(gca, 'XTick',[], 'YTick',[], 'DataAspectRatio',[1,1,1], 'Color',[.67,.7,.9])
% 绘制渐变背景
[X,Y] = meshgrid(1:a, 301:b);
V = repmat(linspace(1, 0, 300)', [1,a]);
t = [0,1]; I = @interp1;
V = cat(3, I(t, [.25,.68], V), I(t, [1/3,.7], V),I(t, [.5,.9], V));
surf(X,Y,X.*0, 'CData',V, 'EdgeColor','none');
% 绘制云彩
P = abs(ifftn(exp(3i*rand(a))./r.^.8)).*(s*s');
C = zeros([a,a,3]);
C(:,:,1) = 1; C(:,:,2) = .75; C(:,:,3) = .88;
y = (1:a)./a.*.8 + .2;
image([0,a], [400,b], C, 'AlphaData',P.*(y'));
% 绘制8座山
c1 = [230,25,90]; c2 = [210,70,10];
for i = 1:8
    H = abs(ifftn(exp(5i*rand(a))./r.^1.05)).*(s*s').*10;
    nh = (8-i)*30 + H(400,:);
    hm = ceil(max(nh));
    C = zeros([hm,a,3]);
    tc = c1 + (c2 - c1)./8.*i;
    tc = hsv2rgb(tc./[360,100,100]);
    C(:,:,1) = tc(1); C(:,:,2) = tc(2); C(:,:,3) = tc(3);
    P = ones(hm,a);
    P((1:hm)' > nh) = nan;
    image([-50,850], [0,hm], C, 'AlphaData',P.*.98);
end

玫瑰花球

function roseball
% author : slandarer
s = @sin; c = @cos; f = @surf;
[x,t] = meshgrid((0:24)./24, (0:.5:575)./575.*20.*pi+4*pi);
p = (pi/2)*exp(-t./(8*pi));
u = 1 - (1 - mod(3.6*t, 2*pi)./pi).^4./2 + s(15*t)/150;
y = 2*(x.^2 - x).^2.*s(p);
r = u.*(x.*s(p) + y.*c(p));
h = u.*(x.*c(p) - y.*s(p)) + .35;
L = [.02 .04 .39; .02 .06 .69; .01 .26 .99; .17 .69 1];
p={'EdgeAlpha',0.05, 'EdgeColor','none', 'FaceColor','interp', 'CData',sH(h,L)};
hold on
x = r.*c(t); y = r.*s(t);
f(x,y,h, p{:})
f(x,y,- h, p{:})
rx = pi - acos(- 1/sqrt(5));
Rx = [1, 0, 0; 0, c(rx), -s(rx); 0, s(rx), c(rx)];
yz = 72*pi/180;
Rz = @(n) [c(yz/n), - s(yz/n), 0; s(yz/n), c(yz/n), 0; 0, 0, 1];
Rz1 = Rz(1); Rz2 = Rz(2);
[U,V,W] = rT(x, y, h, Rx);
for k = 1:5, [U,V,W] = rT(U, V, W, Rz1); f(U, V, W, p{:}), end
[U,V,W] = rT(U, V, W, Rz2);
for k = 1:5, [U,V,W] = rT(U, V, W, Rz1); f(U, V, - W, p{:}), end
axis equal off
view(11, -.07)
    function c = sH(H, cL)
        X = rescale(H, 0, 1);
        c = interp1(rescale(1:size(cL,1), 0, 1), cL, X);
    end
    function [U,V,W] = rT(X, Y, Z, R)
        U = X; V = Y; W = Z;
        for i = 1:numel(X)
            v = [X(i); Y(i); Z(i)];
            n = R*v; U(i) = n(1); V(i) = n(2); W(i) = n(3);
        end
    end
end

MATLAB小游戏截图

以下游戏全部是由本人编写的MATLAB版本的小游戏的截图，不过其中有部分代码为6年前写的代码，可能会极其不优雅。。大家见谅，主要没时间去重构了，以下是小游戏效果截图：

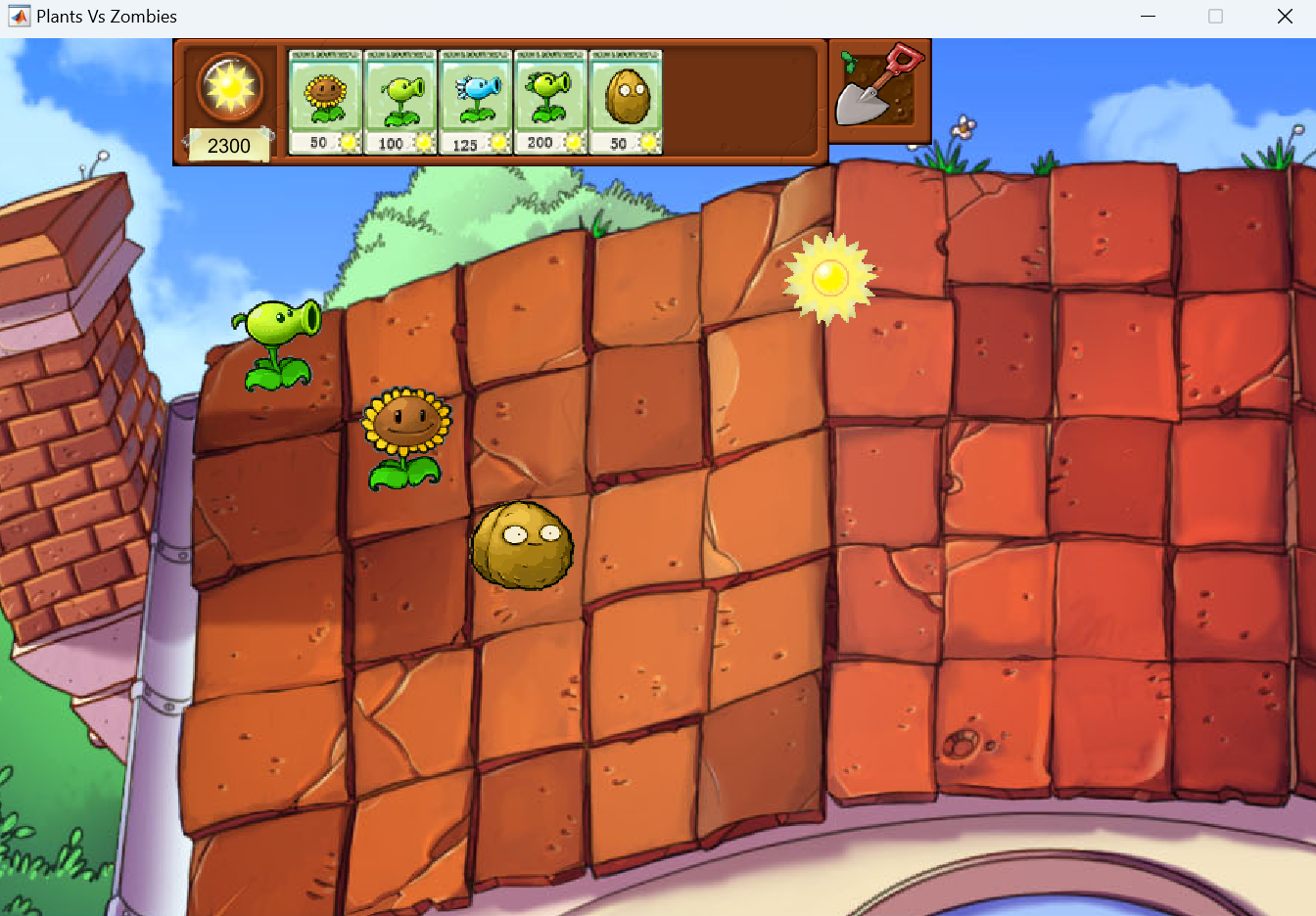
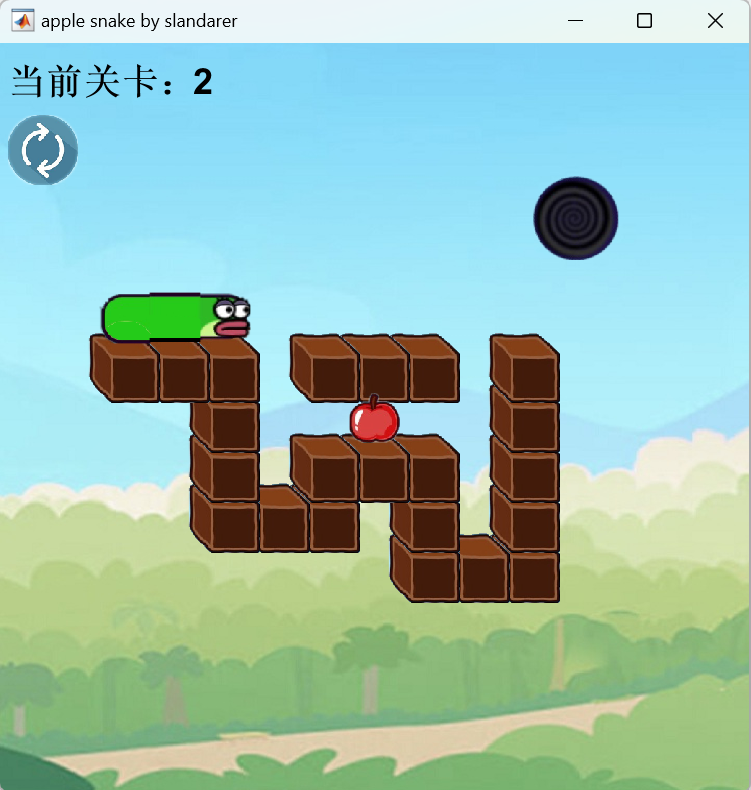
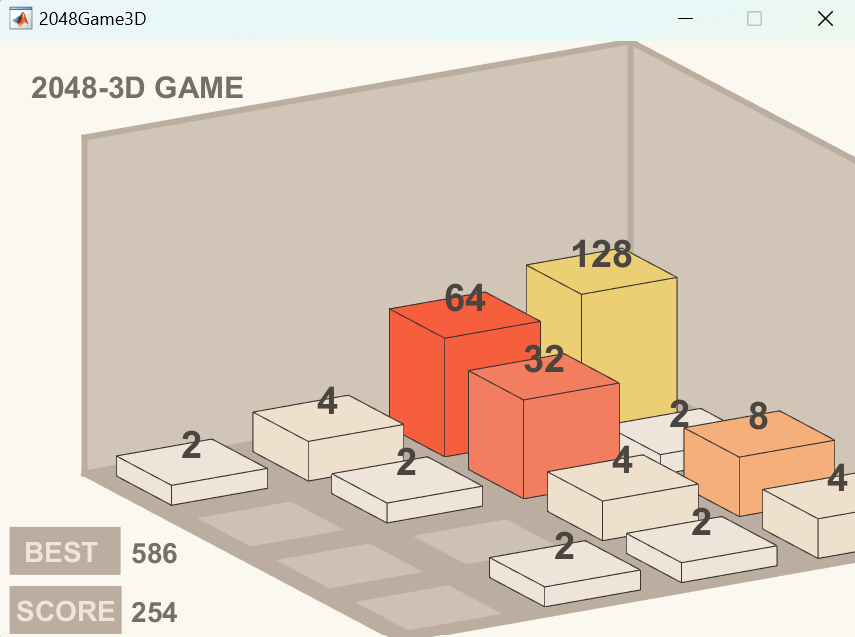
完

以上提到的所有小游戏，以及趣味代码，可在以下网盘链接获取：
链接：https://pan.baidu.com/s/1a1Xd4OQrrYPIuevRNLeNNA?pwd=slan
提取码：slan

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1707192.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【SpringBoot】单元测试实战演示及心得分享

【SpringBoot】单元测试实战演示及心得分享

目录 1.指定测试标准 2.设计测试用例 3.测试集示例 4.跑测试集 1.指定测试标准 单元测试会用到mock和junit的内容，作者前文有详解，可移步： Spring Boot单元测试-CSDN博客 mockito的详细使用-CSDN博客 1.1.测哪一层？ 以当…
阅读更多...
conda 环境找不到 libnsl.so.1

conda 环境找不到 libnsl.so.1

安装prokka后运行报错 perl: error while loading shared libraries: libnsl.so.1: cannot open shared object file: No such file or directory 通过conda list 可以看到 有libsnl 2.00版本，通过修改软链接方式进行欺骗
阅读更多...
K8s集群中的Pod调度约束亲和性与反亲和性

K8s集群中的Pod调度约束亲和性与反亲和性

前言 在 K8s 集群管理中，Pod 的调度约束——亲和性（Affinity）与反亲和性（Anti-Affinity）这两种机制允许管理员精细控制 Pod 在集群内的分布方式，以适应多样化的业务需求和运维策略。本篇将介绍 K8s 集群中…
阅读更多...
【软考】设计模式之外观模式

【软考】设计模式之外观模式

目录 1. 说明2. 应用场景3. 结构图4. 构成5. 适用性6. 优点7. 缺点8. java示例 1. 说明 1.为子系统中的一组接口提供一个一致的界面，Facade模式定义了一个高层接口，这个接口使得这一子系统更加容易使用。2.Facade Pattern。3.是一种结构型设计模式&…
阅读更多...
OM电商系统asp.net

OM电商系统asp.net

OM电商系统，可以让顾客全面了解商品的详细信息，消除网上购物的信息不对称问题。通过商品分类来组织众多的商品，方便顾客找到所需要的商品。提供客服顾客互动机制，提高顾客的参与度。通过设计合理的订单处理流程，提高顾…
阅读更多...
JavaSE：String类常用方法（巨详细）

JavaSE：String类常用方法（巨详细）

1、引言 在学习C语言时，我们就已经了解了字符串，但是在C语言中字符串只能用字符数组或者指针来表示，没有特定的字符串类型，而在Java中，我们有了字符串这一特定的类型---String类。 2、String类的常用方法 2.1 字符串…
阅读更多...
第15章-超声波避障功能 HC-SR04超声波测距模块详解STM32超声波测距

第15章-超声波避障功能 HC-SR04超声波测距模块详解STM32超声波测距

这个是全网最详细的STM32项目教学视频。 第一篇在这里: 视频在这里 STM32智能小车V3-STM32入门教程-openmv与STM32循迹小车-stm32f103c8t6-电赛 嵌入式学习 PID控制算法 编码器电机 跟随 15.1-超声波测距 完成超声波测距功能、测量数据显示在OLED屏幕上 硬件介绍 使用&#…
阅读更多...
OpenHarmony实战开发——宿舍全屋智能开发指南

OpenHarmony实战开发——宿舍全屋智能开发指南

项目说明 基于OpenAtom OpenHarmony（以下简称“OpenHarmony”）、数字管家开发宿舍全屋智能，实现碰一碰开门、碰一碰开灯、碰一碰开风扇以及烟感检测。因为各项目开发流程大体相似，本文主要以碰一碰开门为例介绍如何在现有OpenHar…
阅读更多...
野外作战武器操作3D模拟实操仿真训练以便老兵能适应不同的训练需求

野外作战武器操作3D模拟实操仿真训练以便老兵能适应不同的训练需求

强国必须强军，我国在军事方面的投入持续加大，自然在军事武器培训方面不容忽视，在军事领域，3D模拟展示不仅提升了军事训练的效率，还为我们提供了更加直观、真实的武器体验。 首先，3D军事武器模拟展示能够提供…
阅读更多...
Django革新者：突破传统，构建下一代Web应用

Django革新者：突破传统，构建下一代Web应用

书接上文 —— 家园建筑师：用Django打造你的Web帝国，从前面的学习中，咱们我们经历了一个完整的Django Web开发之旅，涵盖了从基础概念到高级特性的各个方面： 引言：介绍了企业级Web框架的需求，并概…
阅读更多...
分享个自用的 Nginx 加强 WordPress 防护的规则

分享个自用的 Nginx 加强 WordPress 防护的规则

Nginx WordPress 的组合是目前非常普及的组合了，我们完全可以借助 Nginx 规则来加强 WordPress 的防护，提高 WordPress 的安全性，今天明月就给大家分享个自用的 Nginx 针对 WordPress 的防护规则，部分规则大家只需要根据自己的需要…
阅读更多...
ABB焊接功能介绍

ABB焊接功能介绍

1.基本配置 1.2配置Robot Ware Arc 2.焊接语句 2.1直线焊接语句 过渡点指令必须位于起弧指令与熄弧指令之间，不能单独使用。 2.2直线焊接示例 2.3圆弧焊接语句 2.4圆弧焊接示例 2.5摆动参数 关于ABB焊接机器人摆动参数设定 一般情况下，主要设置以…
阅读更多...
[Linux]磁盘管理

[Linux]磁盘管理

一.Linux磁盘管理的原理 磁盘分区与Linux的目录是借助"挂载机制"链接的，将一个分区与一个目录连接起来。访问目录，相当于访问某块分区 lsblk命令: lsblk命令可以查看磁盘分区，以及每个分区所挂载的目录 lsblk -f 可以查看更细节的…
阅读更多...
利用NewGIS平台将FME模板发布为接口

利用NewGIS平台将FME模板发布为接口

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档 前言 一、模板编写 二、发布模板 三、接口获取 四、移动端调用 ​​​​​ 前言 在实际的应用生产过程中，尤其是移动端GIS软件的开发，针对一些闭…
阅读更多...
win11中文文件名称乱码解决方案

win11中文文件名称乱码解决方案

解压后出现以下的乱码 解决方案 步骤1.winR 输入intl.cpl 或 windows 自带的搜索搜“intl.cpl”，打开这个面板控制项 步骤2.在新打开的区域面板中，选择“管理”标签页，点击下方的“更改系统区域设置”按钮 步骤3.取消"Beta版…"选…
阅读更多...
Nginx的配置与调试

Nginx的配置与调试

目录 1、安装Nginx 2、Nginx的配置文件结构 2.1 Nginx的全局配置 2.2 HTTP服务器配置 2.3 HttpGzip模块配置 2.4 负载均衡配置 2.5 server虚拟主机配置 2.6 location URL匹配配置 2.7 StubStatus模块配置 1、安装Nginx 在安装Nginx之前，需确保系统已经安装…
阅读更多...
Day38 代码随想录打卡|二叉树篇---二叉树的最大深度

Day38 代码随想录打卡|二叉树篇---二叉树的最大深度

题目（leecode T104）： 给定一个二叉树 root ，返回其最大深度。 二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。 递归法： 递归法首先将根节点作为参数传入，随后每一轮传入当前节点的…
阅读更多...
【openlayers系统学习】3.3假彩色图像合成（三个波段合成假彩色图像）

【openlayers系统学习】3.3假彩色图像合成（三个波段合成假彩色图像）

三、假彩色图像合成 在上一步中，我们使用 ol/source/GeoTIFF​ 源从单个多波段源（具有红色、绿色、蓝色和Alpha波段）渲染真彩色图像。在下面这个例子中，我们将从可见光谱之外提取数据，并使用它来呈现假彩色合成。 我…
阅读更多...
Linux echo命令（在终端输出文本）

Linux echo命令（在终端输出文本）

文章目录 Linux Echo命令深度解析简介命令语法常见选项- -n：不输出行尾的换行符，这意味着输出后不会换到下一行。- -e：启用反斜杠转义的解释，允许使用特殊字符。- -E：禁用反斜杠转义的解释（默认选项&#x…
阅读更多...
简单得阴影引导实现

简单得阴影引导实现

效果如下: 实现方式： 1、引入三方库： implementation io.github.razerdp:BasePopup:3.2.0 2、代码实现 class NewUserGuide3Popup : BasePopupWindow {constructor(activity: Activity) : super(activity)constructor(context: Context) : super(con…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023