深入浅析卷积核
- 引言
- 单通道卷积
- 简单图像
- 边缘检测
- 锐化
- 高斯滤波
引言
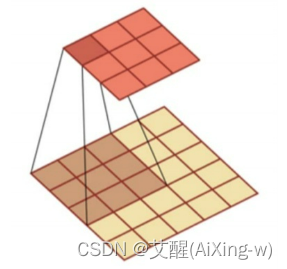
提到卷积,应该多数人都会想到类似上图的这种示例,可以简单的理解成卷积核与图像中和卷积核相同大小的一块区域与卷积核相乘再求和,通过移动区域产生一个有和组成的新的图像,那么卷积核是什么呢,我们来看下面的例子
单通道卷积
首先,我们定义了一个单通道图像的卷积过程,我们用这个来验证卷积核的特性
def Conv2d(X,kernel):
img_row,img_col = X.shape
ker_row,ker_col = kernel.shape
result = torch.zeros(img_row-ker_row+1,img_col-ker_col+1)
res_row,res_col = result.shape
for r in range(res_row):
for c in range(res_col):
result[r,c] = torch.sum(X[r:r+ker_row,c:c+ker_col]*kernel)
return result
简单图像
我们建立两个图像,一个是X一个是Y
X = torch.tensor(
[[1., 0., 0., 0., 0., 0., 1.],
[0., 1., 0., 0., 0., 1., 0.],
[0., 0., 1., 0., 1., 0., 0.],
[0., 0., 0., 1., 0., 0., 0.],
[0., 0., 1., 0., 1., 0., 0.],
[0., 1., 0., 0., 0., 1., 0.],
[1., 0., 0., 0., 0., 0., 1.]])
Y = torch.tensor(
[[1., 0., 0., 0., 0., 0., 1.],
[0., 1., 0., 0., 0., 1., 0.],
[0., 0., 1., 0., 1., 0., 0.],
[0., 0., 0., 1., 0., 0., 0.],
[0., 0., 0., 1., 0., 0., 0.],
[0., 0., 0., 1., 0., 0., 0.],
[0., 0., 0., 1., 0., 0., 0.]])
他们画出图来效果如下
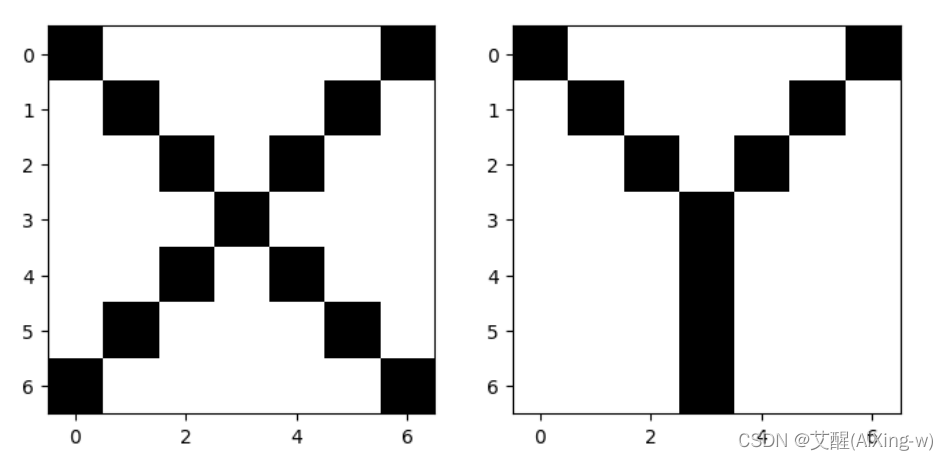
那么如果我们要分类,要通过什么分类呢?
我们观察到X和Y都有左斜向下,右斜向下的特征,但是X又多一个两个线交叉的特征
那么我们可以建立三个卷积核
#卷积核
kernel0=torch.tensor(
[[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
kernel1=torch.tensor(
[[0., 0., 1.],
[0., 1., 0.],
[1., 0., 0.]])
kernel2=torch.tensor(
[[1., 0., 1.],
[0., 1., 0.],
[1., 0., 1.]])
他们三个效果如下
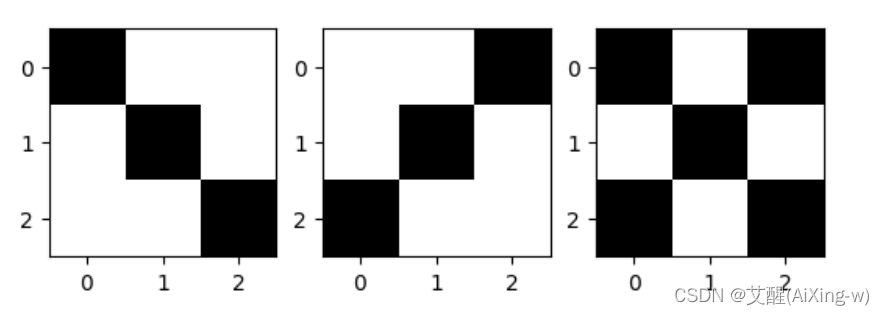
我们对X卷积
X_kernel0 = Conv2d(X,kernel0)
X_kernel1 = Conv2d(X,kernel1)
X_kernel2 = Conv2d(X,kernel2)
plt.subplot(131)
plt.imshow(X_kernel0,cmap='gray_r')
plt.subplot(132)
plt.imshow(X_kernel1,cmap='gray_r')
plt.subplot(133)
plt.imshow(X_kernel2,cmap='gray_r')
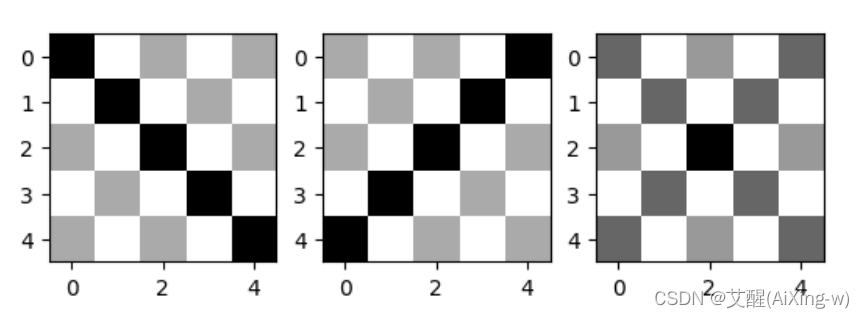
可以看到三个卷积的特征都有被匹配
那么我们来看Y
X_kernel0_ = Conv2d(Y,kernel0_)
X_kernel1_ = Conv2d(Y,kernel1_)
X_kernel2_ = Conv2d(Y,kernel2_)
plt.subplot(131)
plt.imshow(X_kernel0_,cmap='gray_r')
plt.subplot(132)
plt.imshow(X_kernel1_,cmap='gray_r')
plt.subplot(133)
plt.imshow(X_kernel2_,cmap='gray_r')
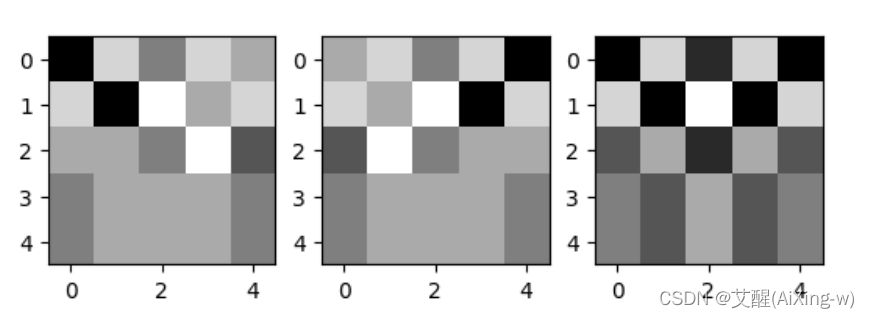
可以看到左上和左下的特征被提取出来了,但是交叉的特征因为Y只有上半部分,所以只有上半部分被匹配上一部分
上面的过程就是卷积核用于提取特征的过程,当然不用担心,这些卷积核只是用于做个案例,实际上深度学习的卷积核的值是由反向传递学习得来,我们不需要担心自己设定卷积核的问题
边缘检测
上面我们在简单的图像中展示了卷积核的作用,下面我们来看一下卷积核在真实图像中是怎样的效果。
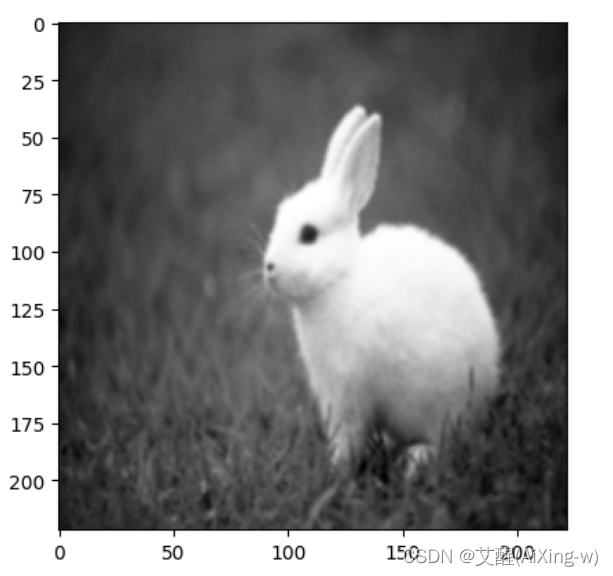
我们假设有这样一张兔子的图片

首先我们用灰度方式读入(下同)
img = cv2.imread('tuzi.jpg', cv2.IMREAD_GRAYSCALE)
plt.imshow(img, cmap=plt.cm.gray)
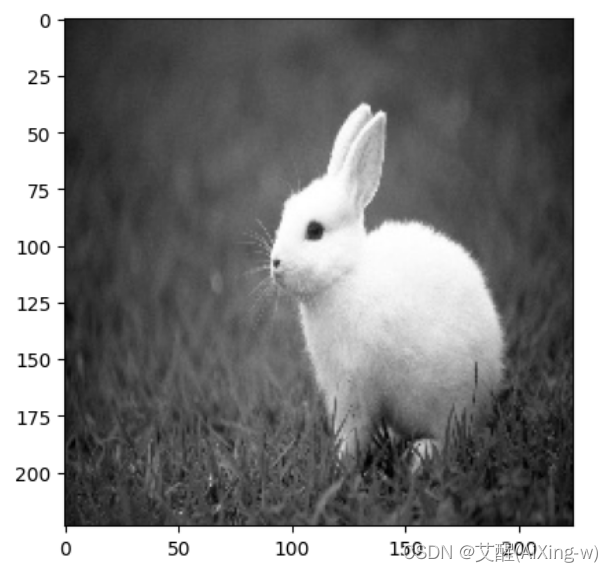
我们想要获得他的边缘,那么就可以使用下面的卷积核
[
−
1
,
−
1
,
−
1
−
1
,
8
,
−
1
−
1
,
−
1
,
−
1
]
\begin{bmatrix} -1 ,-1, -1 \\ -1 , 8 ,-1 \\ -1 ,-1, -1 \end{bmatrix}
−1,−1,−1−1,8,−1−1,−1,−1
这里做一下解释,这个核主要是侧重于中心,只要是中心不是和周围的像素完全一样,经过卷积之后就能得到一个正值,正值越大说明差别越明显,即边界,否则会得到负值或0
kernel_0 = torch.tensor([[-1, -1, -1],
[-1, 8, -1],
[-1, -1, -1]
])
X_kernel_0 = Conv2d(torch.tensor(img), kernel_0)
plt.imshow(X_kernel_0, cmap=plt.cm.gray)
这样我们就得到了兔子的边缘

锐化
锐化需要以下卷积核
[
0
,
−
1
,
0
−
1
,
5
,
−
1
0
,
−
1
,
0
]
\begin{bmatrix} 0 ,-1, 0 \\ -1 , 5 ,-1 \\ 0 ,-1, 0 \end{bmatrix}
0,−1,0−1,5,−10,−1,0
这里可以发现,和之前的边缘检测的卷积核相比,他只注重中心上下左右的像素,并且如果周围像素完全相同他也是会得到正值,这样的效果比边缘检测更加温和,并没有一下子把周围相同的像素完全取代,而是增强与周围差距大的像素点,抑制与周围差距小的像素点
kernel_1 = torch.tensor([[0, -1, 0],
[-1, 5, -1],
[0, -1, 0]
])
X_kernel_1 = Conv2d(torch.tensor(img), kernel_1)
plt.imshow(X_kernel_1, cmap=plt.cm.gray)
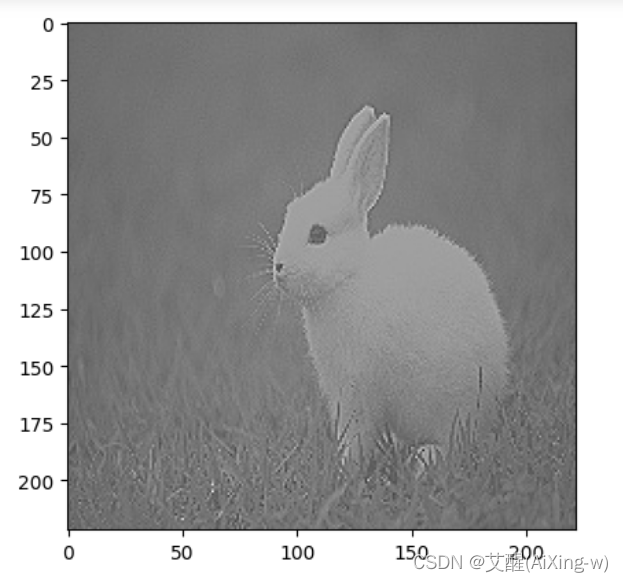
高斯滤波
1
16
[
1
,
2
,
1
2
,
4
,
2
1
,
2
,
1
]
\frac{1}{16}\begin{bmatrix} 1 ,2, 1 \\ 2 , 4 ,2 \\ 1 ,2, 1 \end{bmatrix}
161
1,2,12,4,21,2,1
高斯滤波就是使用符合高斯分布的卷积核,通常用于图像滤波,这里的图片没有高斯噪声,效果不明显,高斯滤波详细内容可以查看
opencv-python常用函数解析及参数介绍(三)——图像滤波
kernel_2 = torch.tensor([[1, 2, 1],
[2, 4, 2],
[1, 2, 1]
]) / 16
X_kernel_2 = Conv2d(torch.tensor(img), kernel_2)
plt.imshow(X_kernel_2, cmap=plt.cm.gray)

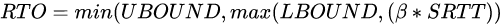




![[网鼎杯 2020 青龙组]AreUSerialz](https://img-blog.csdnimg.cn/99059d6e16cd4d1dad1bd32ef91d2fef.png)