线性回归

---

线性回归的理解

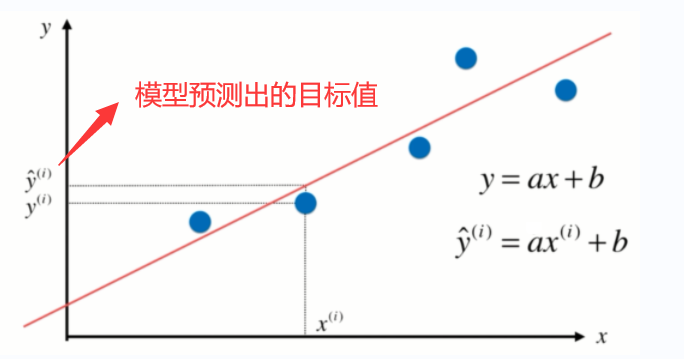
线性回归：判断数据的特征和目标值之间具有一定的线性关系。
简单线性回归：样本的特征只有一个，用线性回归法进行预测，叫做简单线性回归。
多元线性回归：样本的特征有两个或两个以上，叫做多元线性回归。

如下图所示，为线性回归模型

损失函数

损失函数：np.sum((y`-y)**2)，即预测值和真实值的差值之和。因为有复数的存在所以求平方，不用绝对值的原因：用平方方便后续的求导和求极值。

最小二乘法

一些推导过程：





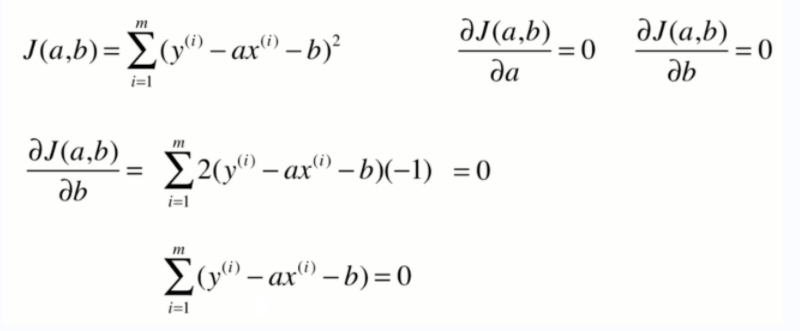
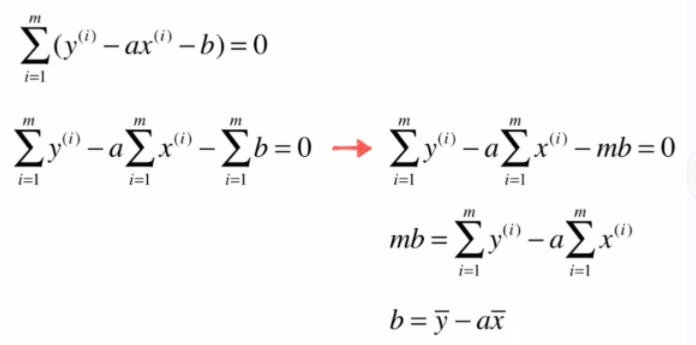
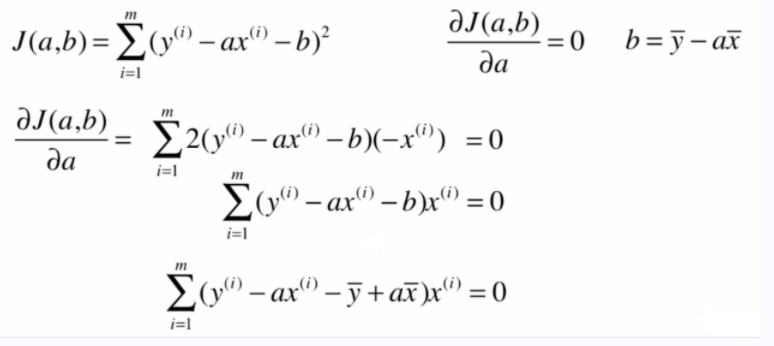
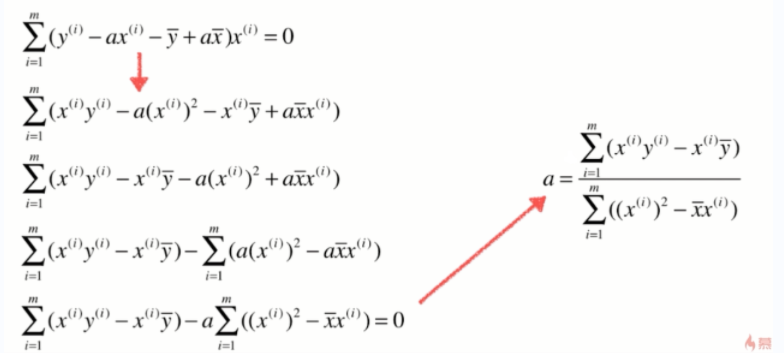
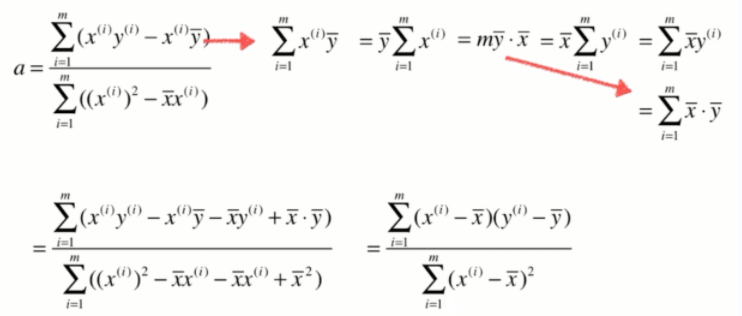
重要结论：

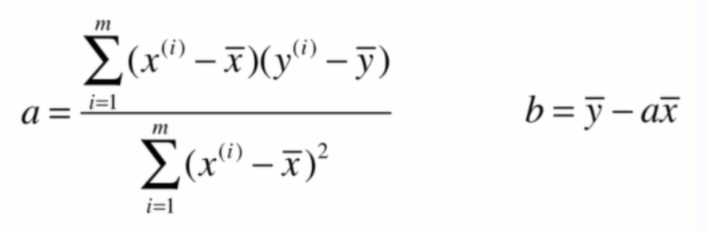
简单线性回归

---

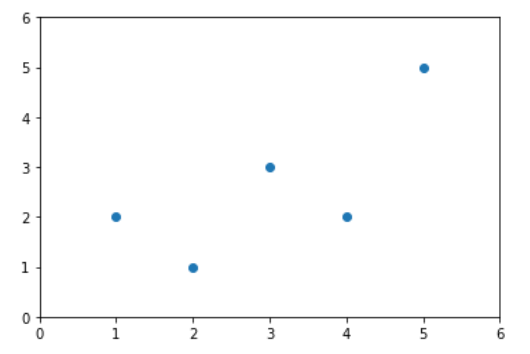
1. 先画出数据的散点图

import numpy as np
import matplotlib.pyplot as plt

x = np.array([1,2,3,4,5])
y = np.array([2,1,3,2,5])

plt.scatter(x,y)
plt.axis([0,6,0,6])
plt.show()

2. 对数据进行处理，求出a和b

# y = a * x + b
# 先求出平均值
x_mean = np.mean(x)
y_mean = np.mean(y)

num = 0.0 # 分子
d = 0.0 # 分母

for x_i, y_i in zip(x, y):
    num += (x_i-x_mean)*(y_i-y_mean)
    d += (x_i-x_mean)**2
a = num/d
b = y_mean-a*x_mean

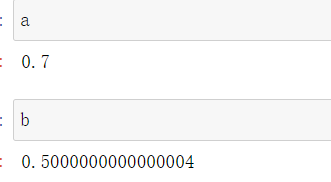
3. 求出y`，并画出预测直线，求出这条线，使得真实值与预测值的差值达到最小。

y_hat = a * x + b

plt.plot(x, y_hat, color='r')
plt.scatter(x,y)
plt.axis([0, 6, 0, 6])
plt.show()

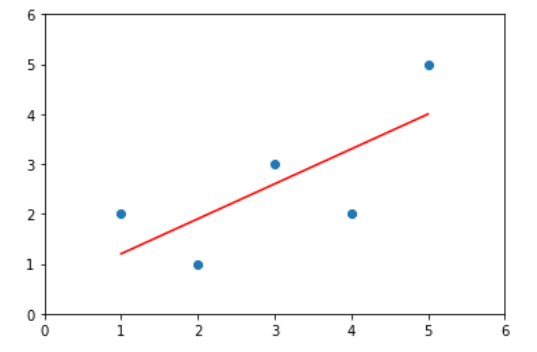
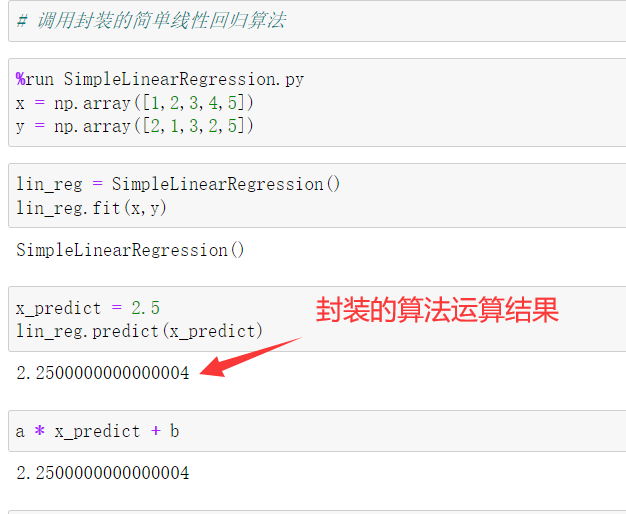
封装线性回归算法

import numpy as np


class SimpleLinearRegression:
    def __init__(self):
        self.a_ = None
        self.b_ = None
        self.x_mean = None
        self.y_mean = None

    def fit(self, x_train, y_train):
        self.x_mean = np.mean(x_train)
        self.y_mean = np.mean(y_train)

        num = 0.0   # 分子
        d = 0.0     # 分母
        for x_i, y_i in zip(x_train, y_train):
            num += (x_i-self.x_mean) * (y_i-self.y_mean)
            d += (x_i-self.x_mean)**2
        self.a = num/d
        self.b = self.y_mean - self.a * self.x_mean

        return self

    def predict(self, x_test):
        return self.a * x_test + self.b

    def __repr__(self):
        return 'SimpleLinearRegression()'

在jupter notebook中导入运行

线性回归算法

---

使用线性回归算法的前提：数据具有一定的线性关系。

我们希望找到一条最佳拟合的直线方程，y=ax+b，对于每一个样本点，在这个直线方程上都有一个预测值，预测值和真实值有一定的差距，我们希望这些样本到直线方程的差距之和最小。

计算差距：sqrt(|y-y`|**2)，使用平方并开根号的方式更适合我们进行求导或求值。

在sklearn中调用线性回归算法

1. 导入模块

from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt

2. 准备数据，训练模型

# 准备数据
x = np.array([1,2,3,4,5])
y = np.array([3,1,4,3,6])

lin_reg = LinearRegression()
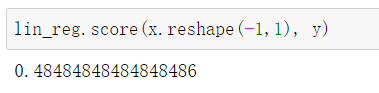
lin_reg.fit(x.reshape(-1,1), y)	# 拟合，训练模型

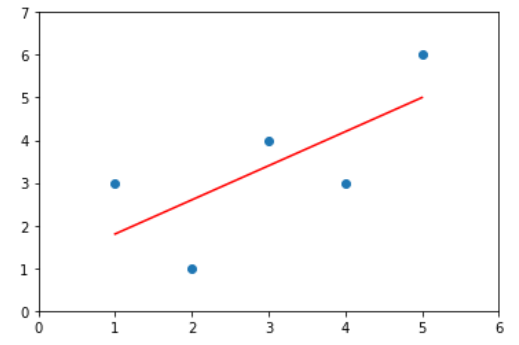
3. 画出散点图和预测直线

plt.scatter(x, y)
plt.plot(x, lin_reg.predict(x.reshape(-1,1)), color='r')
plt.axis([0,6,0,7])
plt.show()

向量化运算

如下图所示，向量化运算更加方便，向量点乘是先乘后加，原理一样。

x = np.array([1,2,3,4,5])
y = np.array([3,1,4,3,6])
def lin_fit(x, y):
    x_mean = np.mean(x)
    y_mean = np.mean(y)
    num = 0.0
    d = 0.0
    num = (x-x_mean).dot(y-y_mean)
    d = (x-x_mean).dot(x-x_mean)
    a = num/d
    b = y_mean-a*x_mean
    return a, b

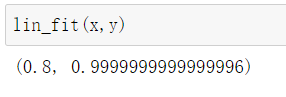
线性回归模型中的误差

---

在分类问题可以将score看成准确率，在回归问题将score看成模型的好坏程度。

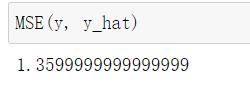
均方误差 MSE

均方误差的公式如下图所示：

为什么要除以样本数量m？
举个例子，比如第一个团队有2个人，统计其工资的均方误差为800，第二个团队有100个人，工资的均方误差为1000，能说明第一个团队比较好吗？这是不行的，因为统计的个数不同，样本不同，导致量纲不一样，所以需要除以样本数量m，减少量纲的影响。

封装的函数

# 均方误差 MSE
def MSE(y_true, y_predict):
    return np.sum((y_true-y_predict)**2)/len(y_true)

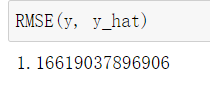
均方根误差

在均方误差中进行开根号处理，可以消除量纲的影响。

封装的均方根误差

# 均方根误差
from math import sqrt
def RMSE(y_true, y_predict):
    return sqrt(np.sum((y_true-y_predict)**2)/len(y_true))

平均绝对误差

封装的平均绝对误差

# 平均绝对误差
def MAE(y_true, y_predict):
    return np.sum(np.absolute(y_true-y_predict))/len(y_true)

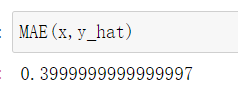
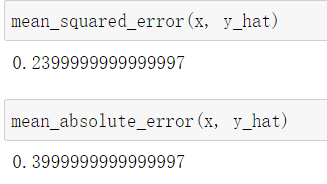
调用sklearn中的均方根误差和平均绝对误差函数

from sklearn.metrics import mean_squared_error, mean_absolute_error
mean_squared_error(x, y_hat)
mean_absolute_error(x, y_hat)

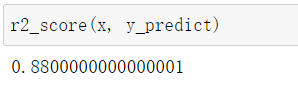
R squared error （常用）

R^2（以下用R2表示）分类的准确度在0和1之间，R2为1时，模型最优，即没有出现任何错误。

计算公式如下：

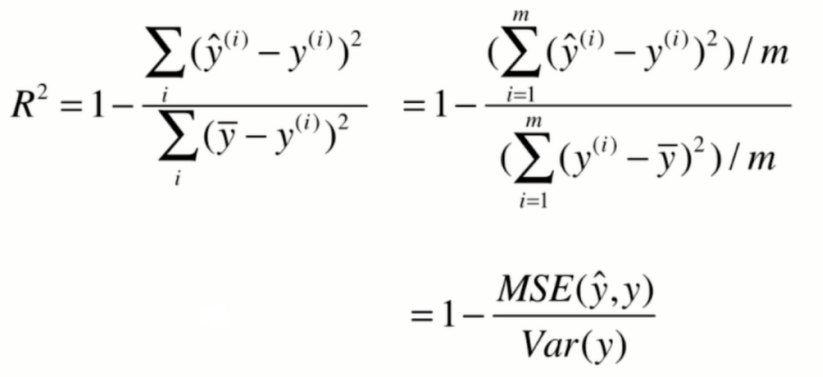
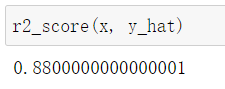
封装R squared error

import numpy as np
x = np.array([1,2,3,4,5])
y = np.array([3,1,4,3,6])
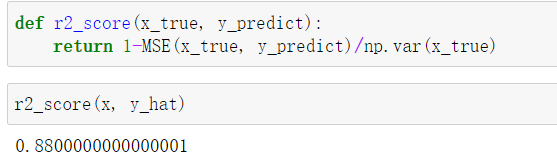
def r2_score(x_true, y_predict):
    return 1-((np.sum((x_true-y_predict)**2)/len(x_true))/np.var(x_true))

或调用均值方差 MSE

调用sklearn中的线性回归算法，计算预测值，最终的误差结果还是一样

from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(x.reshape(-1,1), y)
y_predict = lin_reg.predict(x.reshape(-1,1))