文章目录
- 创建具有特征的二维数据
- 实现SVM算法
- 线性核函数
- 梯度下降和损失函数
- 训练
- 实验效果
- 总结
在前面的章节里,已经简要的介绍了SVM算法的工作原理,现在在这篇文章里,我们来看看SVM算法的一些简单实现。
创建具有特征的二维数据
一般来说,要实现SVM算法对数据的分类任务,我们需要数据至少具备二维的属性(properties)或者标签(attributes)。这里,我们使用numpy中可生成正态分布的随机数生成工具 np.random.normal 大致具体用法如下:
import numpy as np
# 生成随机数据
np.random.seed(0)
# 特征数据1
upper_x = np.random.normal(3, 1.5, (1000, 1))
upper_y = np.random.normal(3, 1.5, (1000, 1))
# 特征数据2
lower_x = np.random.normal(-3, 1.5, (1000, 1))
lower_y = np.random.normal(-3, 1.5, (1000, 1))
# 生成数据集
X = np.concatenate((upper_x, lower_x), axis=0)
y = np.concatenate((upper_y, lower_y), axis=0)
我们把数据PLOT出来看看这些数据生成后是什么样
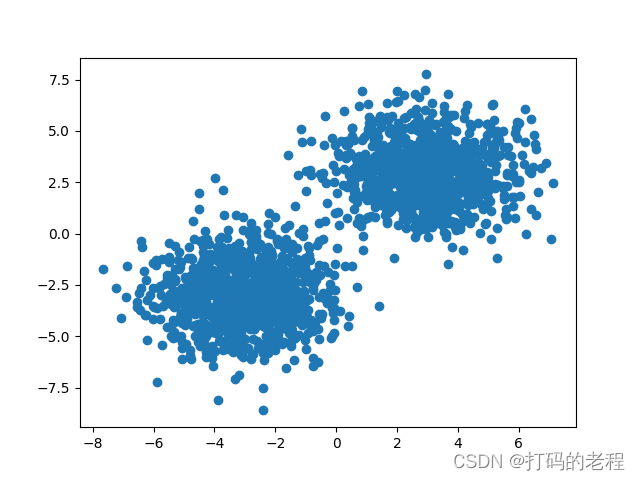
这种样子可以看到大多数数据聚集在两个部分,少部分个别数据可能会有点重合而不是那么明显可以判断出它属于哪一类,这种形态的数据在我们日常数据分析中也是非常常见的一种样子。
实现SVM算法
Python可以使用 scikit-learn 这个库来做大量传统机器学习的任务,但是既然我的系列一直秉承知其然更要知其所以然,所以我们还是一如既往使用最基础的 numpy 工具库来实现我们所有的机器学习算法。
大致上来说,一个SVM算法,主要由以下几部分组成
线性核函数
def linear_kernel(x1, x2):
return np.dot(x1, x2.T)
在前面介绍了SVM分类算法,其中最关键的不是使用什么曲线或者更复杂的方程来实现分类任务,而是十分干脆简单的在不同数据集中找到分类平面。因此对于二维数据,它的分类平面就是线性方程。
梯度下降和损失函数
# 梯度下降与损失函数
def svm_loss(W, X, y, C=1.0):
n_samples, n_features = X.shape
margins = np.maximum(0, 1 - y * np.dot(X, W))
loss = (np.sum(margins) + 0.5 * C * np.dot(W, W)) / n_samples
return loss
def svm_grad(W, X, y, C=1.0):
n_samples, n_features = X.shape
margins = np.maximum(0, 1 - y * np.dot(X, W))
grad = -(np.dot(X.T, y * (margins > 0))) / n_samples + C * W
return grad
这个对于我们非常重要,如果你看过我其他博文,就能知道在较为高等的算法中,为了找到数据最合适的解,我们一般会引入梯度下降算法。
训练
然后就是对实验数据的训练函数
def train(X, y, C=1.0, max_iter=1000, tol=1e-5):
n_samples, n_features = X.shape
W = np.zeros((n_features,))
for i in range(max_iter):
loss = svm_loss(W, X, y, C)
grad = svm_grad(W, X, y, C)
W -= grad
if np.linalg.norm(grad) < tol:
break
return W
然后有了这些重要的组成部分后,我们可以来看看实验效果了
实验效果
首先依然生成一堆随机数据
# 预测
test_x = np.random.normal(0, 1, (100, 1))
test_y = np.random.normal(0, 1, (100, 1))
然后我们实现一个预测函数,其实主要是把上述数据与生成的模型进行乘积,然后结果用正负号进行区分
def predict(X, W):
return np.sign(np.dot(X, W))
pred = predict(test_x, W)
然后把结果绘制出来
# 可视化
import matplotlib.pyplot as plt
plt.scatter(test_x[pred == 1], test_y[pred == 1], c='red')
plt.scatter(test_x[pred == -1], test_y[pred == -1], c='green')
plt.show()
输出图像如下
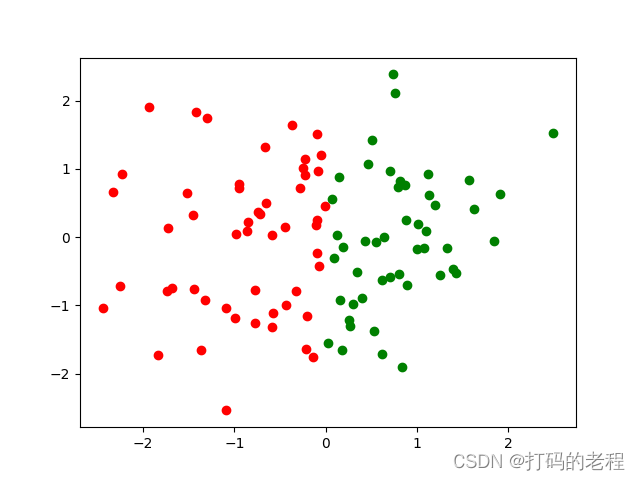
还不错,大致上和我们希望的差不多。当然上述实现方法简单而粗糙,但对于深入理解SVM是怎么工作能有一定的帮助。
总结
此外,如果需要对不平衡的数据进行分类,那么可能需要使用更高级的方法来调整损失函数。例如,对于少数类别,可以使用不同的权重来调整损失函数。
如果需要对高维数据进行分类,那么可能需要使用核技巧来解决该问题。在这种情况下,可以使用高斯核函数代替线性核函数。
如果需要对大规模的数据进行分类,那么可能需要使用分布式计算来解决该问题。在这种情况下,可以使用类似于Apache Spark或Hadoop之类的工具来处理数据。
还有一些其他的因素需要考虑,例如模型的正则化,模型的结构等等,在实际应用中需要根据具体情况来调整参数和数据的处理方式。
此外,如果你希望使用更高级的优化算法来训练模型,例如拉格朗日乘数法或者共轭梯度法,也不是不可以,但是吧到这种情况自己实现起来特别复杂,所以最好还是直接使用工具库比较好点。