indexOf底层使用的方法是典型的BF算法。
1、KMP算法
由来
外国人: Knuth,Morris和Pratt发明了这个算法,然后取它三个的首字母进行了命名。所以叫做KMP。
KMP真的很难理解,建议多看几遍 B站代码随想录,文章也的再好
用处
时间复杂度O(n)
主要应用在 字符串匹配中
最长公共前后缀
将字符串拆分成以首字符开始的各个子串,然后依次判断,下标 n与下标 length - n - 1的元素是否相等,若有 m个连续相等的字符,则最长公共前缀为 m
例如字符串:AABAAF的公共前后缀长度如下图所示,红色代表不相同,蓝色代表元素相同
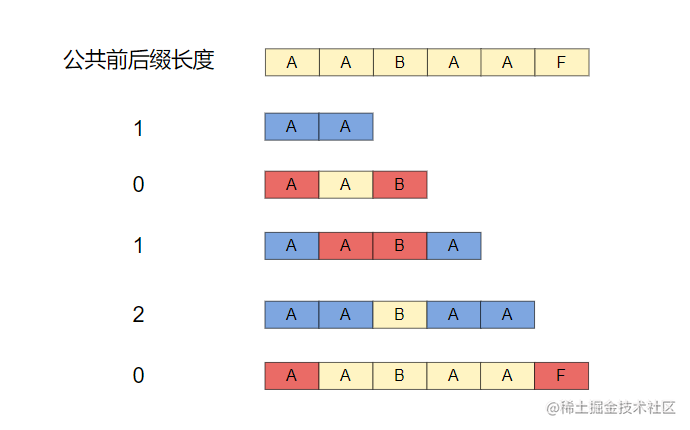
知道了公共前缀, 相应的可以利用我们获取到的公共前缀表来找到当字符不匹配的时候指针应该移动的位置,如下图所示:
下图来自于 代码随想录

核心:next数组
next数组就是用来存储公共前缀的个数的, 例如上面的例子,他的next数组结果就应该是
int[] next = {0,1,0,1,2,0}
复制代码
思路分析
- 前置条件, 字符串 s,前缀数组 int[] next
- 设置一个整数 j代表最长公共前后缀的个数
- 首先是初始化,我们的 next数组第一个元素肯定是 0
- 然后去 for循环我们的字符串,这里需要注意的是我们的for循环是从下标 1开始的
- 判断 j必须大于 0不然的话在回溯过程中会发生 越界的情况,还要判断元素是否相等
-
- 若不相等则 j回溯到上一个 next数组下标
- 这里需要注意的是要用 while循环,因为可能会一直进行回溯操作
- 当 s.charAt(j) == s.charAt(i)时,代表最长前后缀元素个数 +1,所以 j++
- 最后将 j的值赋给数组 next[i]
代码展示
public static int KMP(String s, String p) {
int slen = s.length();
int plen = p.length();
char[] str = s.toCharArray();
char[] ptr = p.toCharArray();
int[] next = new int[plen];
cal_next(ptr, next);
int k = -1;
for (int i = 0; i < slen; i++) {
while (k > -1 && ptr[k + 1] != str[i]) //ptr和str不匹配,且k>-1(表示ptr和str有部分匹配)
k = next[k]; //往前回溯
if (ptr[k + 1] == str[i])
k ++;
if (k == plen - 1) { //说明k移动到ptr的最末端
return i - plen + 1; //返回相应的位置
}
}
return -1;
}
public static void cal_next(char[] str, int[] next) {
int len = str.length;
next[0] = -1; //next[0]初始化为-1,-1表示不存在相同的最大前缀和最大后缀
int k = -1; //k初始化为-1
//如果下一个不同,那么k就变成next[k],注意next[k]
for (int q = 1; q <= len - 1; q++) {
while (k > -1 && str[k + 1] != str[q]) { //是小于k的,无论k取任何值。
k = next[k]; //往前回溯
}
if (str[k + 1] == str[q]) { //如果相同,k++
k ++;
}
next[q] = k; //这个是把算的k的值(就是相同的最大前缀和最大后缀长)赋给next[q]
}
public static void main(String[] args) {
long start = System.currentTimeMillis();
String full = "BBC ABCDAB ABCDABCDABDE";
String par = "ABCDABD";
int res = KMP(full,par);
//int res = full.indexOf(par);
System.out.println(res+","+(System.currentTimeMillis() - start)+"ms");
} |
2、BF与RK算法
2.1 BF算法
BF算法就是Brute Force,暴力匹配算法,也成为朴素匹配算法,主串的大小是sourceSize,模式串的大小是targetSize,因为我们要在主串中查找模式串,所以sourceZize > targetSize,所以从主串下标为0开始,连续查找targetSize个字符,再从下标为1开始后,一直到,下标为sourceSize - targetSize ,举个简单的例子在ABCDEFG中查找EF:

上图依次表示从i为0,到i为4时的依次比较,从图中我们也可以看出,BF算法是比较耗时的,因为比较的次数较多,但是实际比较的时候主串和模式串都不会太长,所以这种比较的方法更容易使用。
现在我们回过头看看indexOf的下半部分源码,我相信其实不用解释了。
2.2 RK算法
RK算法其实就是对BF算法的升级,还是以上面的图为例,在ABCDEFG中查找EF的时候,比如下标为0的时候,我们去比较A和E的值,不相等就不继续往下比较了,但是比如我们现在查找CDF是否在主串中存在,我们要从C已知比较大E发现第三位不相等,这样当模式串前一部分等于主串,只有最后一位不相等的时候,比较的次数太多了,效率比较低,所以我们可以采用哈希计算来比较,哈希计算 后面我会补充一篇。
我们要将模式串和sourceSize - targetSize + 1 个字符串相比,我们可以先将sourceSize - targetSize + 1个模式串进行哈希计算。与哈希计算后的模式串相比较,如果相等则存在,对于哈希冲突在一般实现中概率比较低,不放心的话我们可以在哈希值相等时候再比较一次原字符串确保准确,哈希的冲突概率也和哈希算法的本身设计有关。这样的话,我们首先计算AB的哈希值 与 模式串的相比较,然后计算BC的哈希值与模式串相比较,直到比较出相等的返回下标即可。
3、String.index源码
使用的测试代码如下所示
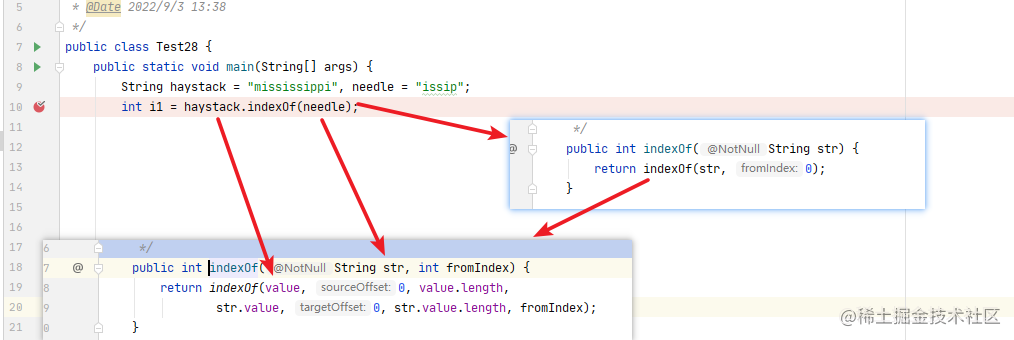
String haystack = "mississippi", needle = "issip"; int i1 = haystack.indexOf(needle); 对应的源码方法重载跳转如下所示:
- 先进入 indexOf(String str)方法
- 跳转进入 indexOf(String str, int fromIndex)
-
- 这个时候 fromIndex == 0
- 跳转进入 inexOf(char[] source, int sourceOffset, int sourceCount, char[] target, int targetOffset, int targetCount, int fromIndex)
-
- value表示 haystack元素的 char数组
- value.length表示 haystack的长度
- str.value表示 needle元素的 char数组
- str.value.length表示 needle的长度
- 接下来我们看 indexOf方法的具体实现

String.indexOf()方法详解
因为我没有下载 java8源码,所以直接在这里进行注释标注了
// source: 当前字符串元素
// sourceOffset: 偏移量
// sourceCount: 当前字符串长度
// target: 目标字符串
// targetOffset:目标字符串偏移量
// targetCount: 目标字符串长度
// fromIndex: 索引位置
static int indexOf(char[] source, int sourceOffset, int sourceCount,
char[] target, int targetOffset, int targetCount,
int fromIndex) {
if (fromIndex >= sourceCount) {
return (targetCount == 0 ? sourceCount : -1);
}
if (fromIndex < 0) {
fromIndex = 0;
}
// 如果目标字符串的长度为 0则直接返回 索引位置 (我们这里因为之前方法重载 fromIndex为 0 所以返回 0)
if (targetCount == 0) {
return fromIndex;
}
// 获取目标 首字符
char first = target[targetOffset];
// 我们这里就是 源字符串长度 - 目标字符串长度, sourceOffset == 0
int max = sourceOffset + (sourceCount - targetCount);
// 循环,i == 0
// 加入循环到了 max的索引位置还没有找到和 目标字符串首字符相等的元素,则源字符串中肯定不包含目标字符串
for (int i = sourceOffset + fromIndex; i <= max; i++) {
// 搜索首字符所在位置
if (source[i] != first) {
while (++i <= max && source[i] != first);
}
// 找到了首字符,判断其余字符位置是否相等
if (i <= max) {
int j = i + 1;
// 根据目标字符串的长度截取源字符串从下标 i开始相同长度的字符串
int end = j + targetCount - 1;
// 遍历判断
for (int k = targetOffset + 1; j < end && source[j]
== target[k]; j++, k++);
// 如果到最后一个元素都相同,则代表源字符串内包含目标字符串
if (j == end) {
// 这里就直接返回了 i 因为源字符串偏移量为 0
return i - sourceOffset;
}
}
}
return -1;
}时间复杂度O(n*m)
4、为什么Java String.indexOf ()没有使用更加“高效”的字符串搜索算法
为什么Java String indexOf 没有使用更加“高效”的算法
参考:
java - Why does String.indexOf() not use KMP? - Stack Overflow
原来JDK的编写者们认为大多数情况下,字符串都不长,使用原始实现可能代价更低。
因为KMP和Boyer-Moore算法都需要预先计算处理来获得辅助数组,需要一定的时间和空间,这可能在短字符串查找中相比较原始实现耗费更大的代价。在短字符串测试过程中,使用indexOf方法时要比KMP算法要快一点。KMP算法对与超长字符串子匹配速度上是优于IndexOf的。
因为KMP算法需要预先计算处理来获得辅助数组,需要一定的时间和空间,这可能在短字符串查找中相比较原始实现耗费更大的代价。
而且一般大字符串查找时,程序员们也会使用其它特定的数据结构,查找起来更简单。这有点类似于排除特定情况下的快速排序了。不同环境选择不同算法。
5、总结起来有两点:
- ① 高效的算法BM和KMP都是需要空间作为代价的,特别是BM,任何一个字符串都需要至少64K内存,考虑到L1 Cache大小,cost更不可知。
- ② JDK应该默认了不会使用Java String.indexOf查找过大的字符串,对于轻量级(通常不超过几十个字符),及时暴力用时也非常短。这也提示,Java String.indexOf的客户端程序员应该对于自己使用的API有所了解,如果要进行过大的字符串查找,应该自己设计算法(取出两个字符串的value[],然后实现BM或KMP)或调用第三方工具专门处理。
6、参考
java - Why does String.indexOf() not use KMP? - Stack Overflow
efficiency - Why does Java's String class not implement a more efficient indexOf()? - Software Engineering Stack Exchange
从 KMP算法到 Java的 String.indexOf(String str)方法-阿里云开发者社区
字符串匹配算法从indexOf函数讲起 - 腾讯云开发者社区-腾讯云
字符串匹配算法总结 (分析及Java实现)_数据中国的博客-CSDN博客
KMP算法——字符串快速匹配_AAMahone的博客-CSDN博客