一、Topk问题
1、问题描述
TOP-K问题:即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。
比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
2、思路
对于Top-K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了(可能
数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决,基本思路如下:
1. 用数据集合中前K个元素来建堆
前k个最大的元素,则建小堆
前k个最小的元素,则建大堆
2. 用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素
将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
3、代码实现
首先通过文件函数生成100000个数据:
void CreateNDate()
{
// 造数据
int n = 100000;
srand(time(0));
const char* file = "data.txt";
FILE* fin = fopen(file, "w");
if (fin == NULL)
{
perror("fopen error");
return;
}
for (int i = 0; i < n; ++i)
{
int x = (rand() + i) % 10000000;
fprintf(fin, "%d\n", x);
}
fclose(fin);
}在前面我们了解到若为向下建堆则为O(N);而向上建堆为O(N*logN);所以我们在这采用向下建堆:
void AdjustDown(HPDataType* a, int n, int parent)
{
// 先假设左孩子小
int child = parent * 2 + 1;
while (child < n) // child >= n说明孩子不存在,调整到叶子了
{
// 找出小的那个孩子
if (child + 1 < n && a[child + 1] < a[child])
{
++child;
}
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}void TestHeap3()
{
int k;
printf("请输入k>:");
scanf("%d", &k);
int* kminheap = (int*)malloc(sizeof(int) * k);//开辟空间
if (kminheap == NULL)
{
perror("malloc fail");
return;
}
const char* file = "data.txt";//打开我们刚刚创建的文件
FILE* fout = fopen(file, "r");
if (fout == NULL)
{
perror("fopen error");
return;
}
// 读取文件中前k个数
for (int i = 0; i < k; i++)
{
fscanf(fout, "%d", &kminheap[i]);
}
// 建K个数的小堆
for (int i = (k - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(kminheap, k, i);
}
// 读取剩下的N-K个数
int x = 0;
while (fscanf(fout, "%d", &x) > 0)
{
if (x > kminheap[0])
{
kminheap[0] = x;//堆顶数据始终是最小的不可能出现卡住数据进不去问题
AdjustDown(kminheap, k, 0);
}
}
printf("最大前%d个数:", k);
for (int i = 0; i < k; i++)
{
printf("%d ", kminheap[i]);
}
printf("\n");
}
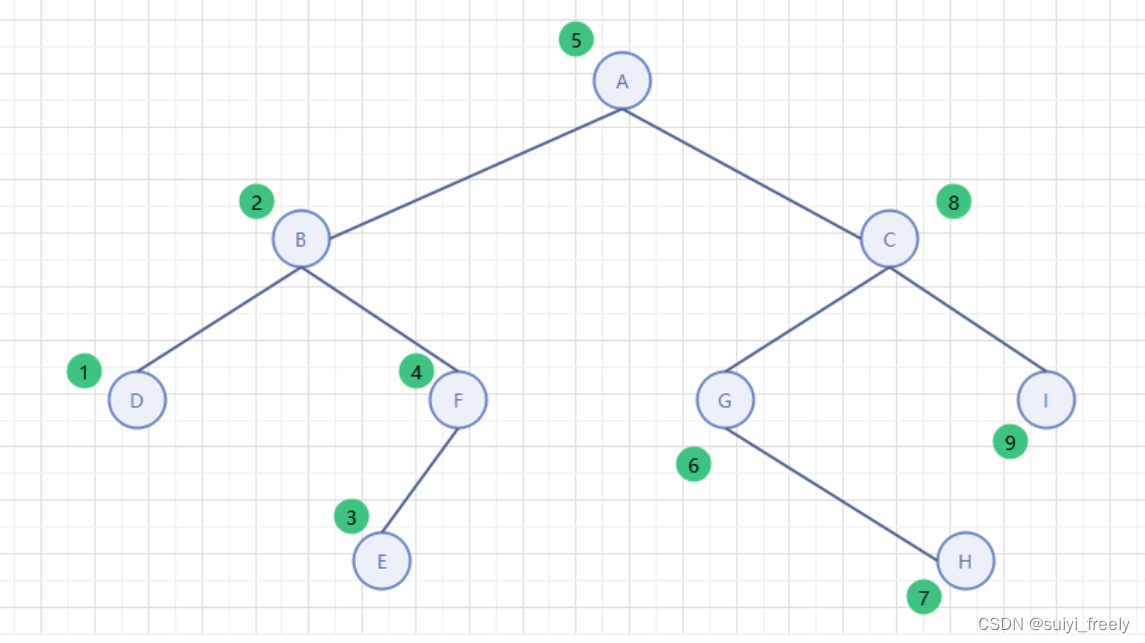
二、二叉树的三种层序遍历
以下三种遍历,如果树的深度太深就会栈溢出。
1、二叉树前序遍历
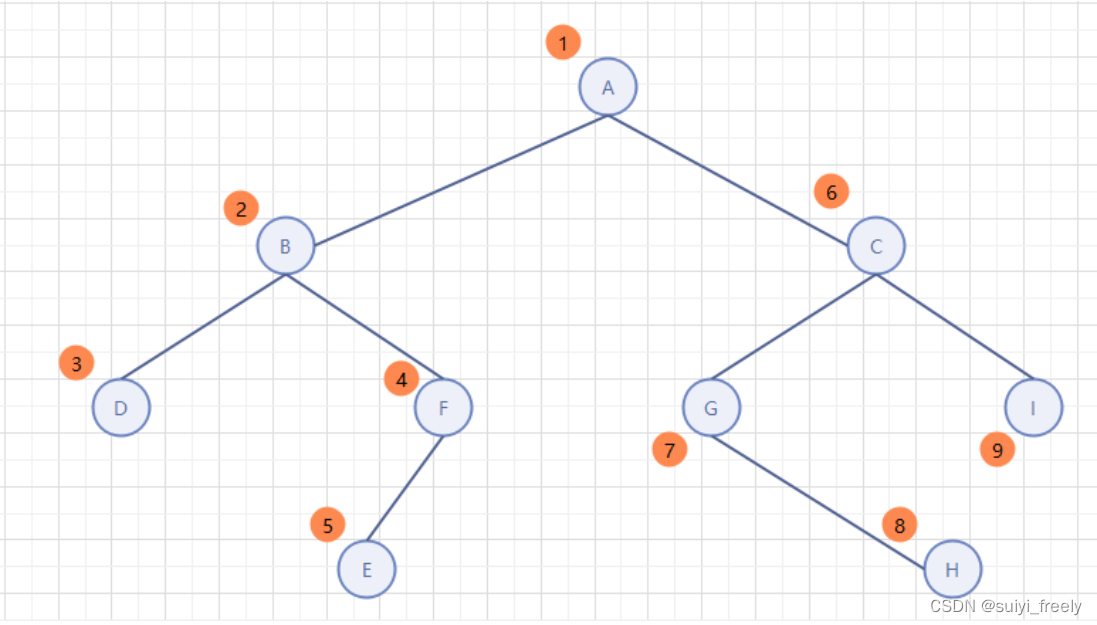
void PreOrder(BTNode* root)
{
if (root == NULL)
{
printf(" null ");
return;
}
printf("%d ", root->_data);
PreOrder(root->_left);
PreOrder(root->_right);
}递归调用图: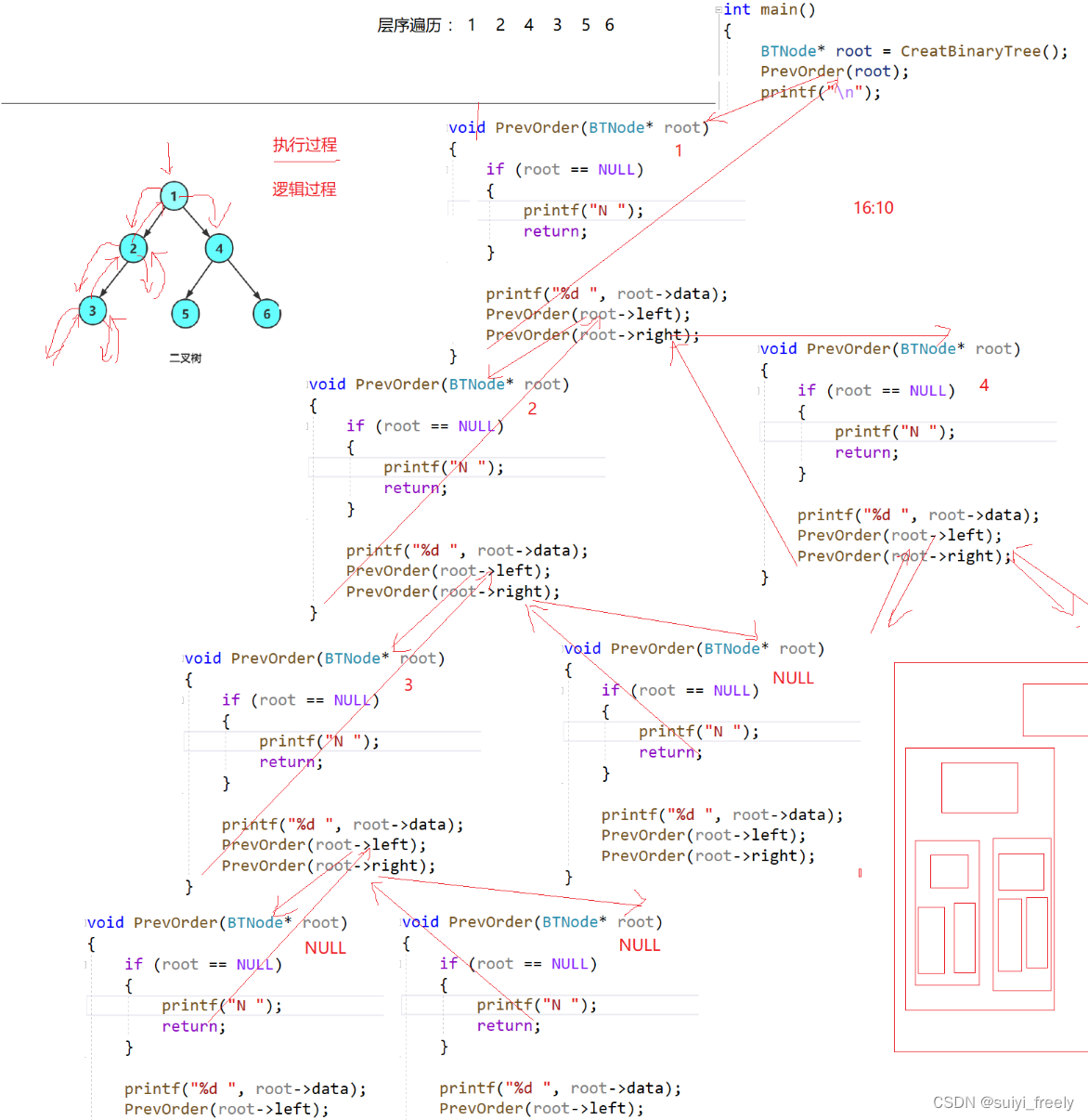
剩下的两种遍历流程图与其类似,这里不做详细图解。
2、二叉树中序遍历
// 二叉树中序遍历
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf(" null ");
return;
}
InOrder(root->_left);
printf("%d ", root->_data);
InOrder(root->_right);
}3、二叉树的后序遍历
// 二叉树后序遍历
void PostOrder(BTNode* root)
{
if (root == NULL)
{
printf(" null ");
return;
}
PostOrder(root->_left);
PostOrder(root->_right);
printf("%d ", root->_data);
}三、树相关的计算
1、节点数的计算
节点数的计算可分为左树+右树 +1;
int treesize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
return treesize(root->_left) + treesize(root->_right);
}2、叶字节点数
为空,叶为0,非空为左叶子数+右叶子数,结束条件为该节点左右两个子节点为空,或者该节点为空
int treeleaf(BTNode* root)
{
if (root == NULL)
{
return 0;
}
if (root->_left == NULL && root->_right == NULL)
{
return 1;
}
return treeleaf(root->_left) + treeleaf(root->_right);
}3、深度
若为空则高度为0,非空为左数高度与右数高度大的那一个
int treeleafhigh(BTNode* root)
{
if (root == NULL)
{
return 0;
}
int lefthigh = treeleafhigh(root->_left) + 1;
int righthigh = treeleafhigh(root->_right) + 1;
if (lefthigh > righthigh)
{
return lefthigh;
}
else
{
return righthigh;
}
}