默认路由实现两个网段互通实验

**默认路由：**是一种特殊的静态路由，当路由表中与数据包目的地址没有匹配的表项时，数据包将根据默认路由条目进行转发。默认路由在某些时候是非常有效的，例如在末梢网络中，默认路由可以大大简化路由器的配置，减轻网络管理员的工作负担。

命令为：ip route-static 0.0.0.0 0.0.0.0 x.x.x.x

0.0.0.0 0.0.0.0： 代表任何网络，也就是说任何数据包都转发给配置的下一跳路由器接口地址 让下一个路由器继续处理数据包。

x.x.x.x：下一跳路由接口地址。

网络拓扑图如下：

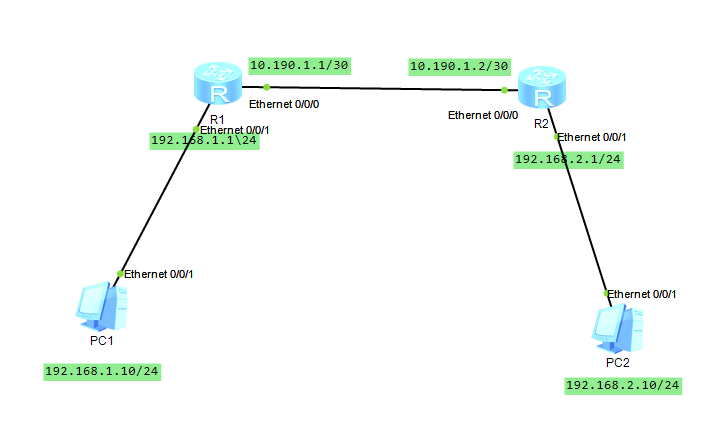
由拓扑图我们可以知道需要进行以下步骤：

1.配置PC1和PC2

PC1

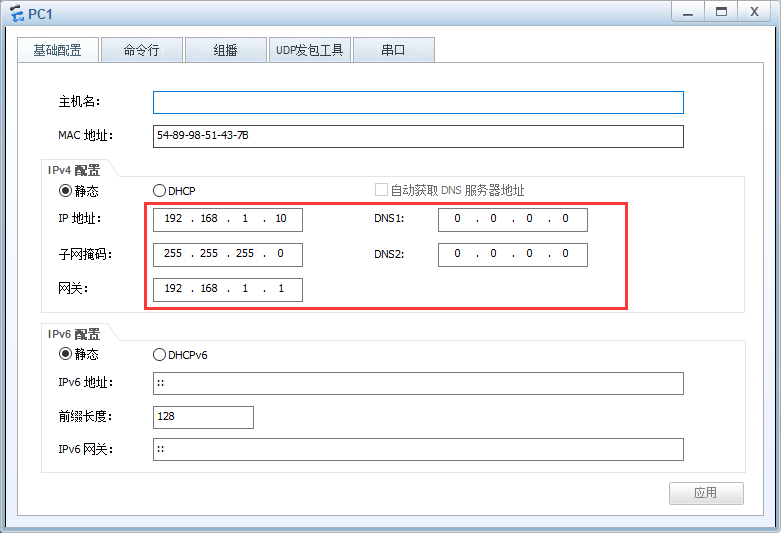
PC2

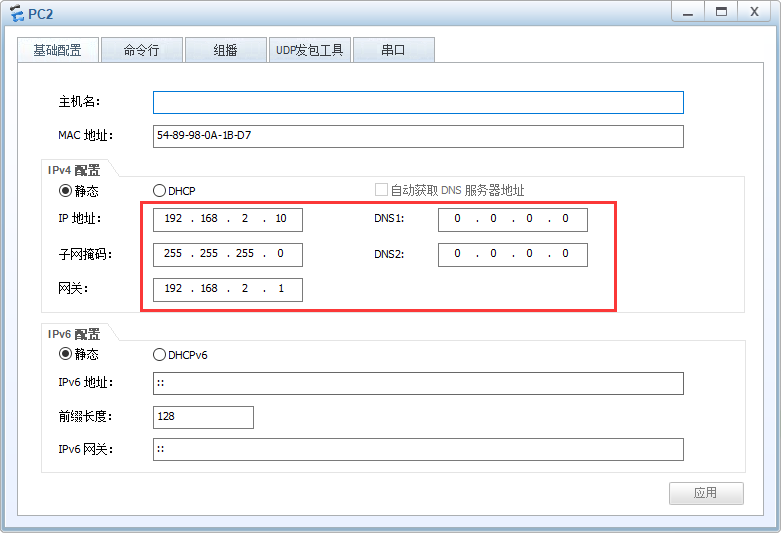
2.配置以太网接口的IP地址

R1

interface e 0/0/1
ip address 192.168.1.1 255.255.255.0
q
interface e 0/0/0
ip address 10.190.1.1 255.255.255.252

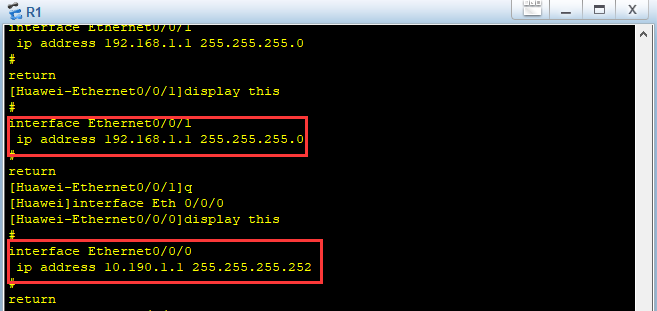
R2

interface e 0/0/1
ip address 192.168.2.1 255.255.255.0
q
interface e 0/0/0
ip address 10.190.1.2 255.255.255.252

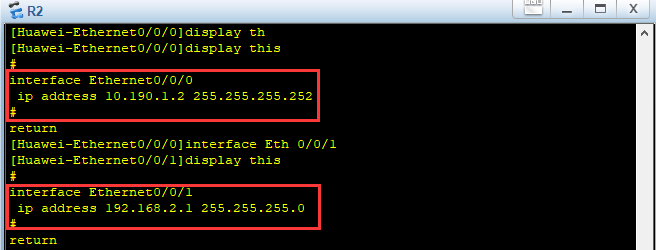
3.配置R1和R2的默认路由

R1

ip route-static 0.0.0.0 0.0.0.0 10.190.1.2

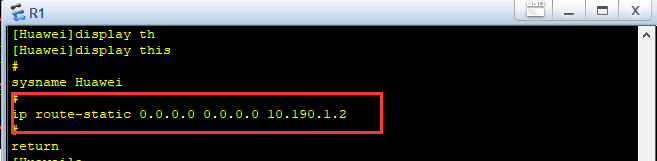
R2

ip route-static 0.0.0.0 0.0.0.0 10.190.1.1

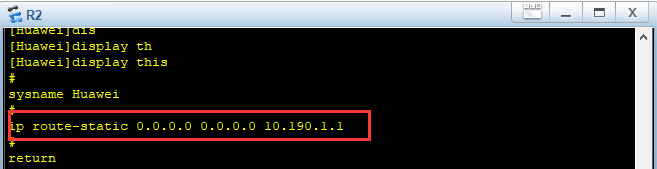
4.使用PC1pingPC2