题意
求:在所有 n n n 个点 m m m 条边的无向简单连通图中,满足把第 i i i 个点删去后图被分为 a i a_i ai 个连通块。
n − 1 ≤ m ≤ n + 1 n-1\le m\le n+1 n−1≤m≤n+1。
思路
将 m = n − 1 , m = n , m = n + 1 m=n-1,m=n,m=n+1 m=n−1,m=n,m=n+1 三种情况进行分类讨论。
对于
m
=
n
−
1
m=n-1
m=n−1,显然是一棵树,每个
a
i
a_i
ai 即为
i
i
i 的子树数量+父亲。此时需要用到 Prufer 序列(可以看看这篇博客),答案为:
n
n
n 个点的完全生成树中第
i
i
i 个节点的度数为
a
i
a_i
ai 的方案数,即为:
(
n
−
2
)
!
∏
i
=
1
n
(
a
i
−
1
)
!
\cfrac{(n-2)!}{\prod^n_{i=1}(a_i-1)!}
∏i=1n(ai−1)!(n−2)!
当
m
=
n
m=n
m=n 时,相当于在树上加上一条边形成一个环。我们把环上的边都删除,开一个编号为
n
+
1
n+1
n+1 的新点与环上的点连边。这样原图就又转化成了一棵
n
+
1
n+1
n+1 个点
n
n
n 条边的树,而第
n
+
1
n+1
n+1 个点的度数为环上点的个数。举个例子:
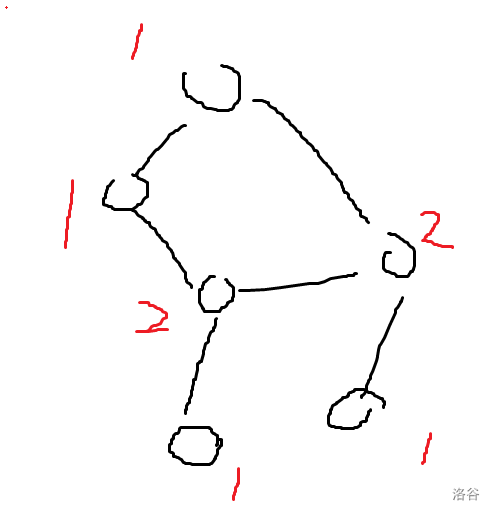
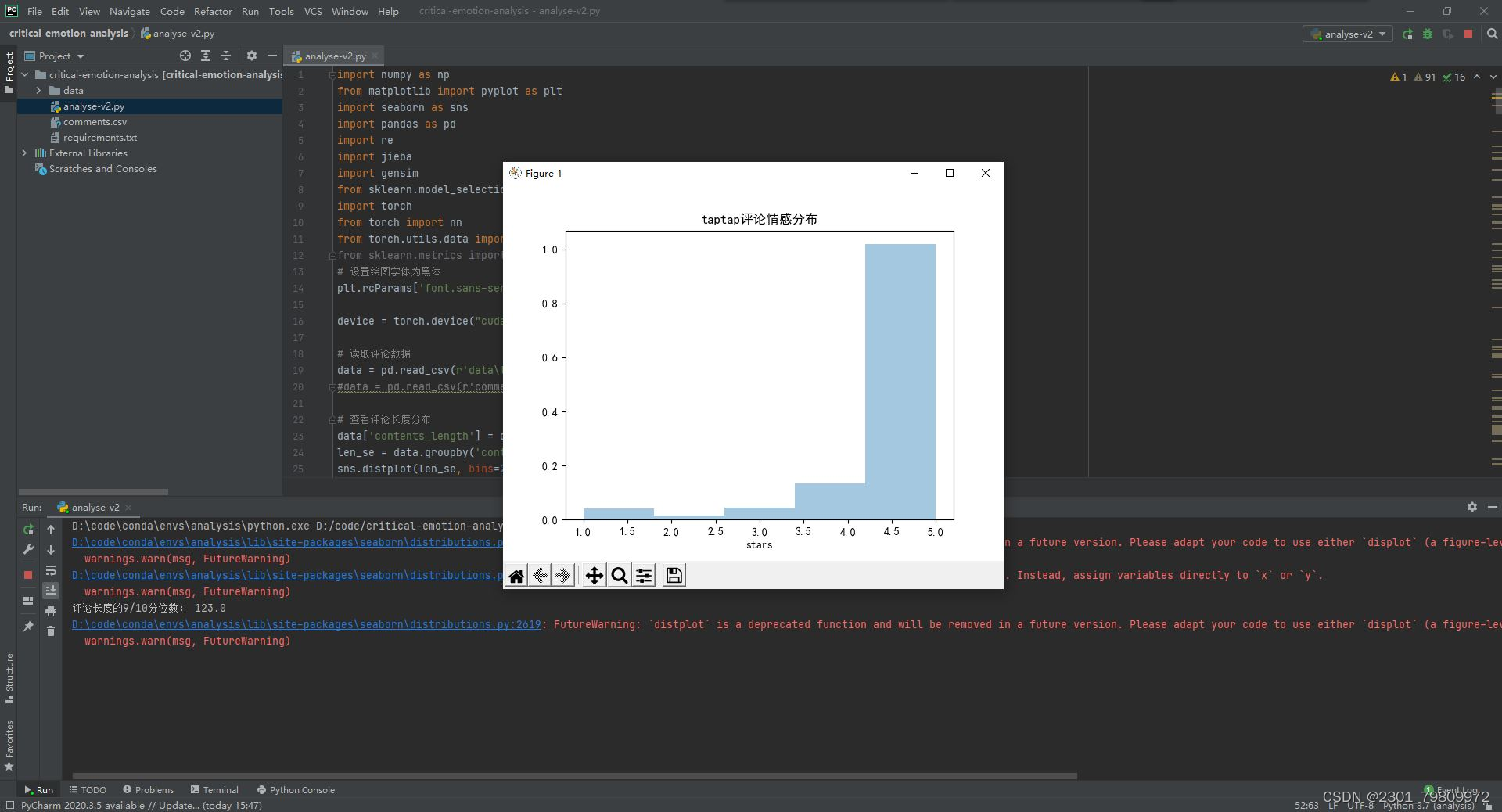
- 这是一张 6 6 6 个点 6 6 6 条边的图,其中红色数组代表 a i a_i ai 的值。而环的大小为 4 4 4
可以发现:环的大小就是点数乘二再减去度数之和,即
a
n
+
1
=
2
n
−
∑
i
=
1
n
a
i
a_{n+1}=2n-\sum^n_{i=1}a_i
an+1=2n−i=1∑nai
根据上一种情况,再乘上环上点的排列方案
A
a
n
+
1
a
n
+
1
2
a
n
+
1
=
(
2
n
−
(
∑
i
=
1
n
a
i
)
−
1
)
!
2
\cfrac{A^{a_{n+1}}_{a_{n+1}}}{2a_{n+1}}=\cfrac{\big(2n-(\sum^n_{i=1}a_i\big)-1)!}{2}
2an+1Aan+1an+1=2(2n−(∑i=1nai)−1)!,答案即为
(
n
−
1
)
!
(
∏
i
=
1
n
(
a
i
−
1
)
!
)
(
2
n
−
(
∑
i
=
1
n
a
i
)
−
1
)
!
×
(
2
n
−
(
∑
i
=
1
n
a
i
)
−
1
)
!
2
=
(
n
−
1
)
!
2
∏
i
=
1
n
(
a
i
−
1
)
!
\begin{aligned}&~~~~~\cfrac{(n-1)!}{\big(\prod^n_{i=1}(a_i-1)!\big)(2n-\big(\sum^n_{i=1}a_i)-1\big)!}\times\cfrac{(2n-(\sum^n_{i=1}a_i)-1)!}{2}\\&=\cfrac{(n-1)!}{2\prod^n_{i=1}(a_i-1)!}\end{aligned}
(∏i=1n(ai−1)!)(2n−(∑i=1nai)−1)!(n−1)!×2(2n−(∑i=1nai)−1)!=2∏i=1n(ai−1)!(n−1)!
当
m
=
n
+
1
m=n+1
m=n+1 时,相当于在上一种情况再多加一个环。进行分类讨论:
- 两个环无公共边
此时我们可以将两个环分别缩成 n + 1 , n + 2 n+1,n+2 n+1,n+2 两个点,仿照 m = n m=n m=n 进行连边,最终会得到 n + 2 n+2 n+2 个点 n + 1 n+1 n+1 条边的树。再举个例子:

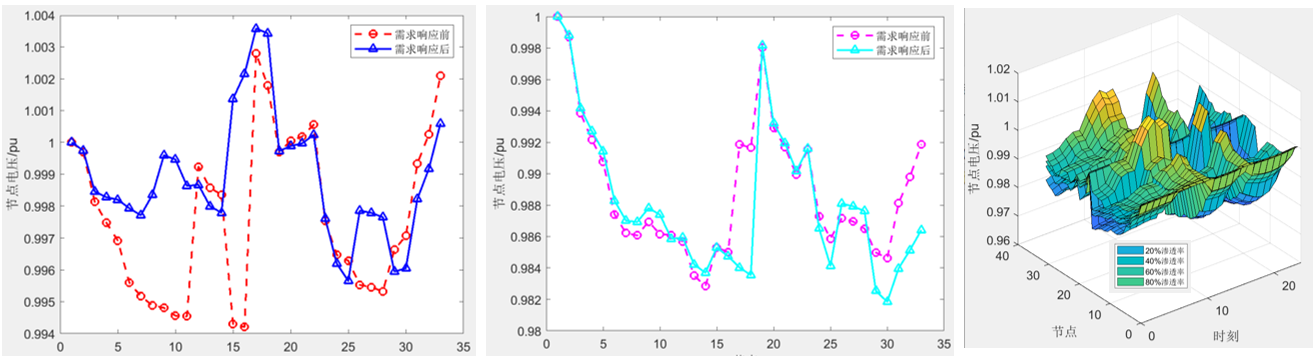
- 这是一张 9 9 9 个点 10 10 10 条边的图,左环大小为 5 5 5,右环大小为 4 4 4。
区别在于,此时只能算出两个环的大小之和,答案类似,即
a
n
+
1
+
a
n
+
2
=
2
n
−
∑
i
=
1
n
a
i
+
2
a_{n+1}+a_{n+2}=2n-\sum^n_{i=1}a_i+2
an+1+an+2=2n−i=1∑nai+2
我们设
2
n
−
∑
i
=
1
n
a
i
=
s
u
m
2n-\sum^n_{i=1}a_i=sum
2n−∑i=1nai=sum。两点的度数都至少为
3
3
3(否则不成环),我们枚举
a
n
+
1
a_{n+1}
an+1 为
j
j
j,则
a
n
+
2
=
s
u
m
+
2
−
j
a_{n+2}=sum+2-j
an+2=sum+2−j。仿照
m
=
n
−
1
m=n-1
m=n−1 的求法,此时树的数量为
(
n
+
2
−
2
)
!
∏
i
=
1
n
+
2
(
a
i
−
1
)
!
=
n
!
(
∏
i
=
1
n
(
a
i
−
1
)
!
)
(
j
−
1
)
!
(
s
u
m
−
j
+
1
)
!
\cfrac{(n+2-2)!}{\prod^{n+2}_{i=1}(a_i-1)!}=\cfrac{n!}{\big(\prod^n_{i=1}(a_i-1)!\big)(j-1)!(sum-j+1)!}
∏i=1n+2(ai−1)!(n+2−2)!=(∏i=1n(ai−1)!)(j−1)!(sum−j+1)!n!
但我们需要保证
n
+
1
n+1
n+1 与
n
+
2
n+2
n+2 在树中无连边(即两个环没有公共点,否则就变成一个环了)。对于有连边的情况,我们按照
m
=
n
m=n
m=n 建出
n
+
1
n+1
n+1 个点
n
n
n 条边的树来,则这棵树的
a
n
+
1
=
s
u
m
a_{n+1}=sum
an+1=sum,树的数量即为
(
n
−
1
)
!
(
∏
i
=
1
n
(
a
i
−
1
)
!
)
(
2
n
−
(
∑
i
=
1
n
a
i
)
−
1
)
!
=
(
n
−
1
)
!
(
∏
i
=
1
n
(
a
i
−
1
)
!
)
(
s
u
m
−
1
)
!
\cfrac{(n-1)!}{\big(\prod^n_{i=1}(a_i-1)!\big)\big(2n-(\sum^n_{i=1}a_i)-1\big)!}=\cfrac{(n-1)!}{\big(\prod^n_{i=1}(a_i-1)!\big)(sum-1)!}
(∏i=1n(ai−1)!)(2n−(∑i=1nai)−1)!(n−1)!=(∏i=1n(ai−1)!)(sum−1)!(n−1)!
而这样的树每个都有
C
s
u
m
j
−
1
=
s
u
m
!
(
s
u
m
−
j
+
1
)
!
(
j
−
1
)
!
C^{j-1}_{sum}=\cfrac{sum!}{(sum-j+1)!(j-1)!}
Csumj−1=(sum−j+1)!(j−1)!sum! 种,则所有不合法的树的数量为
(
n
−
1
)
!
(
∏
i
=
1
n
(
a
i
−
1
)
!
)
(
s
u
m
−
1
)
!
×
s
u
m
!
(
s
u
m
−
j
+
1
)
!
(
j
−
1
)
!
\cfrac{(n-1)!}{\big(\prod^n_{i=1}(a_i-1)!\big)(sum-1)!}\times\cfrac{sum!}{(sum-j+1)!(j-1)!}
(∏i=1n(ai−1)!)(sum−1)!(n−1)!×(sum−j+1)!(j−1)!sum!
化简得
(
n
−
1
)
!
s
u
m
(
∏
i
=
1
n
(
a
i
−
1
)
!
)
(
j
−
1
)
!
(
s
u
m
−
j
+
1
)
!
\cfrac{(n-1)!sum}{\big(\prod^n_{i=1}(a_i-1)!\big)(j-1)!(sum-j+1)!}
(∏i=1n(ai−1)!)(j−1)!(sum−j+1)!(n−1)!sum
使用容斥,所有合法的树的数量等于所有减去不合法,即为
(
n
−
1
)
!
(
n
−
s
u
m
)
(
∏
i
=
1
n
(
a
i
−
1
)
!
)
(
j
−
1
)
!
(
s
u
m
−
j
+
1
)
!
\cfrac{(n-1)!(n-sum)}{\big(\prod^n_{i=1}(a_i-1)!\big)(j-1)!(sum-j+1)!}
(∏i=1n(ai−1)!)(j−1)!(sum−j+1)!(n−1)!(n−sum)
同理,还要算上两个环的排列方案共
(
j
−
1
)
!
(
s
u
m
−
j
+
1
)
!
4
\cfrac{(j-1)!(sum-j+1)!}{4}
4(j−1)!(sum−j+1)!,则答案为
(
n
−
1
)
!
(
n
−
s
u
m
)
(
∏
i
=
1
n
(
a
i
−
1
)
!
)
(
j
−
1
)
!
(
s
u
m
−
j
+
1
)
!
×
(
j
−
1
)
!
(
s
u
m
−
j
+
1
)
!
4
\cfrac{(n-1)!(n-sum)}{\big(\prod^n_{i=1}(a_i-1)!\big)(j-1)!(sum-j+1)!}\times\cfrac{(j-1)!(sum-j+1)!}{4}
(∏i=1n(ai−1)!)(j−1)!(sum−j+1)!(n−1)!(n−sum)×4(j−1)!(sum−j+1)!
化简得
(
n
−
1
)
!
(
n
−
s
u
m
)
4
∏
i
=
1
n
(
a
i
−
1
)
!
\cfrac{(n-1)!(n-sum)}{4\prod^{n}_{i=1}(a_i-1)!}
4∏i=1n(ai−1)!(n−1)!(n−sum)
最终我们发现对于不同的
j
j
j 最终答案相同,一共枚举了
s
u
m
+
2
−
3
−
3
+
1
=
s
u
m
−
3
sum+2-3-3+1=sum-3
sum+2−3−3+1=sum−3 次,考虑到两个环位置可以调换但属同一种情况,所以答案要除以二,即为
(
n
−
1
)
!
(
n
−
s
u
m
)
(
s
u
m
−
3
)
8
∏
i
=
1
n
(
a
i
−
1
)
!
\cfrac{(n-1)!(n-sum)(sum-3)}{8\prod^{n}_{i=1}(a_i-1)!}
8∏i=1n(ai−1)!(n−1)!(n−sum)(sum−3)
- 两个环有公共边
将这两个挨在一起的环看作一个点,构造一个与 m = n m=n m=n 时的树,树的数量也相同。现在考虑这挨在一起的两个环的方案。我们可以将这两个环拆成类似韦恩图的样子,分为左边环独有部分、左右环公用部分、右边环都有部分三条链。因为要有公共边,所以有两条及以上的链中边数不大于 1 1 1 显然不合法。而这三条链头尾都是相同的。
因为环挨在一起,所以这两个环上节点一共有
s
u
m
=
2
n
−
∑
i
=
1
n
a
i
sum=2n-\sum^n_{i=1}a_i
sum=2n−∑i=1nai 个点。我们先从
s
u
m
sum
sum 中挑两个点出来,之后的每个点都选择两个位置放在中间,不合法数量(即之后的所有点全都放在一条链上)即为
3
(
s
u
m
−
2
)
!
3(sum-2)!
3(sum−2)!;而放入点的顺序并不影响最终答案。故答案为
s
u
m
(
s
u
m
−
1
)
2
×
s
u
m
!
2
−
3
(
s
u
m
−
2
)
!
3
!
=
s
u
m
!
24
(
s
u
m
(
s
u
m
−
1
)
−
6
)
=
s
u
m
!
24
(
s
u
m
+
2
)
(
s
u
m
−
3
)
\begin{aligned}\cfrac{sum(sum-1)}{2}\times\cfrac{\frac{sum!}{2}-3(sum-2)!}{3!}&=\cfrac{sum!}{24}(sum(sum-1)-6)\\&=\cfrac{sum!}{24}(sum+2)(sum-3)\end{aligned}
2sum(sum−1)×3!2sum!−3(sum−2)!=24sum!(sum(sum−1)−6)=24sum!(sum+2)(sum−3)
再乘上树的数量,答案为
s
u
m
(
s
u
m
+
2
)
(
s
u
m
−
3
)
(
n
−
1
)
!
24
∏
i
=
1
n
(
a
i
−
1
)
!
\cfrac{sum(sum+2)(sum-3)(n-1)!}{24\prod^n_{i=1}(a_i-1)!}
24∏i=1n(ai−1)!sum(sum+2)(sum−3)(n−1)!
两种情况分别计算,最后相加即可。复杂度
O
(
n
)
O(n)
O(n)。
实现
预处理出阶乘,逆元用快速幂计算,三种情况分别处理即可。
代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int maxn = 1e6 + 5;
const int P = 998244353;
int n,m; ll a[maxn]; ll pro[maxn];
ll inv(ll x) {
int y = P - 2; ll res = 1;
while (y) {
if (y & 1) res = (res * x) % P;
x = (x * x) % P, y >>= 1;
}
return res;
}
int main() {
pro[0] = pro[1] = 1;
for (ll i = 2;i <= maxn - 5;i ++)
pro[i] = (pro[i - 1] * i) % P;
scanf("%d%d",&n,&m);
if (m == n - 1) { // 1
ll tmp = 1;
for (int i = 1;i <= n;i ++)
scanf("%lld",&a[i]),
tmp = (tmp * pro[a[i] - 1]) % P;
printf("%lld",pro[n - 2] * inv(tmp) % P);
} else if (m == n) { // 2
ll tmp = 2;
for (int i = 1;i <= n;i ++)
scanf("%lld",&a[i]),
tmp = (tmp * pro[a[i] - 1]) % P;
printf("%lld",pro[n - 1] * inv(tmp) % P);
} else { // 3
ll sum = n * 2 % P, tmp = 1;
for (int i = 1;i <= n;i ++)
scanf("%lld",&a[i]),
sum -= a[i], tmp = (tmp * pro[a[i] - 1]) % P;
ll ans1 = ((pro[n - 1] * (n - sum) % P) * (sum - 3) % P) * inv(tmp * 8 % P) % P;
ll ans2 = ((((pro[n - 1] * (sum + 2) % P) * (sum - 3) % P) * sum) % P) * inv(tmp * 24 % P) % P;
printf("%lld",(ans1 + ans2) % P);
}
return 0;
}