二叉树——堆详解

news2024/7/6 19:01:24

目录

前言：

一、堆的结构

二、向上调整和向下调整

        2.1 向上调整

        2.2 向下调整

        2.3 向上调整和向下调整时间复杂度比较

三、堆的实现

        3.1 堆的初始化

        3.2 堆的销毁

        3.3 堆的插入

                3.4堆的删除

        3.5 取堆顶元素

        3.6 对堆判空

四、堆排序

五、TOP-K 问题

 六、代码总览

        heap.h

heap.c

test.c(推排序和TOP-K问题）

最后

前言：

        之前我们已经学习过了二叉树的基本知识，接下来我们就要上些“硬菜”了，话不多说，开始我们今天的学习吧！

一、堆的结构

        前文我们已经交待了什么为堆？以及堆的分类。我们既然已经对上文的基础知识已经明白，那么我们现在就来探讨以下如何实现一个堆。

         我们想，数据在内存中的存放是不是连续的，不以人的意志为改变，对吧。堆，是一个完全二叉树，在内存的存放不存在中间为空的情况。所以，咱们可以以数组的方式来存储堆。以下，是堆的结构：

struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}；

        看起来和我们之前的顺序表结构有些类似。虽然，我们知道了其结构，但是我们不知道如何存储呀！要是随便存储，那和普通数组，普通二叉树有何区别。为了能够实现堆，我们将采取以下的方法。

二、向上调整和向下调整

        2.1 向上调整

                什么是向上调整呢？对于一个二叉树，我们知道了孩子节点，我们是不是可以反推出父节点。经行比较，小的成为父亲（建小堆），大的成为孩子，这样进行一一比较，小堆是不是就建好了。

                向上调整就是：谁小谁当爹，谁大谁儿子，就这么简单。代码实现如下：

void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[parent] > a[child])
		{
			sweap(&a[parent], &a[child]);//注意：这里一定要传地址，&不要忘记
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

                相信大家的sweap函数都能够独立实现，这里就不在展示，要是无法实现可参考文末处代码。

        2.2 向下调整

                向下调整是基于一个建好的堆来经行实现的，为啥？向上调整从子节点调，那向下调整是不是应该从父节点开始调。要是这个堆一会是大堆，一会是小堆，那还能调吗？肯定是不行了呀。所以：向下调整健堆的前提是：左右子树必须是一个堆，才能调整。

                其实现思路和向上调整类似，这里直接来看代码：

void AdjustDown(HPDataType* a, int n, int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		if (a[child] > a[child+1])//此步的目的是找到最小的
		{
			child++;
		}
		if (a[parent] > a[child])
		{
			sweap(&a[parent], &a[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

                有了向上调整，对于向下调整大家应该可以理解。

        2.3 向上调整和向下调整时间复杂度比较

                我们说了这么多肯定要考虑其效率问题，我们对于时间复杂度的关注度是一如既往的深。大家会有这样的感觉：这两个时间复杂度应该一样吧，都是O（N*logN）。大家先别急，我给大家推一遍就明白了：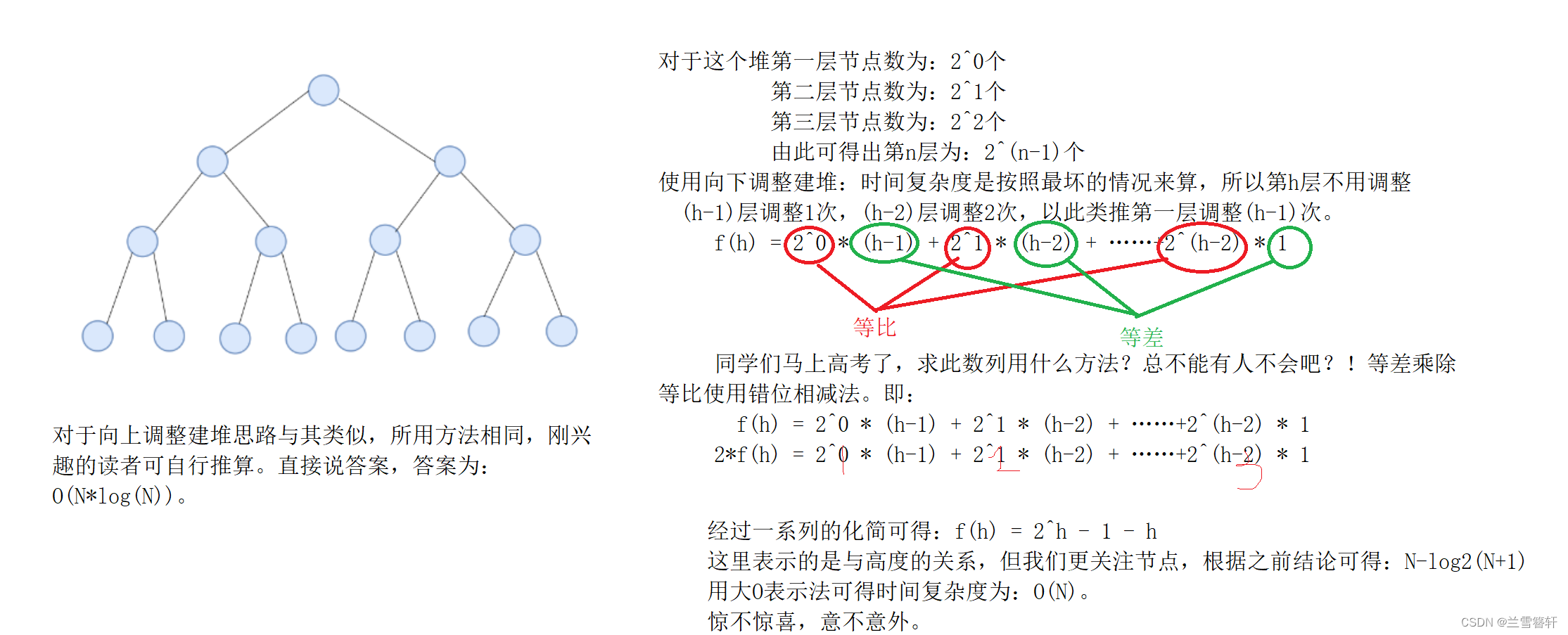

        它们的时间复杂度为什么会有差别呢？很简单，向下调整建堆是用小成大，大乘小。向上调整建堆是用小乘小，大乘大。所以会有这样的差距。从效率上看 ，向下调整建堆的效率大于向上调整建堆。在后文推排序中所用的方法为：向下调整。

三、堆的实现

        既然我们的方法都已具备，那我们现在就拿下堆吧！

        3.1 堆的初始化

void HeapInit(Heap* php)
{
	assert(php);
	php->a = NULL;
	php->capacity = php->size = 0;
}

        3.2 堆的销毁

void HeapDestory(Heap* hp)
{
	assert(hp);
	free(hp->a);
	hp->a = NULL;
	hp->capacity = hp->size = 0;
}

        3.3 堆的插入

void sweap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}
void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[parent] > a[child])
		{
			sweap(&a[parent], &a[child]);//注意：这里一定要传地址，&不要忘记
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}
void HeapPush(Heap* hp, HPDataType x)
{
	assert(hp);
	if (hp->capacity == hp->size)
	{
		int newcapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;
		HPDataType* newnode = (HPDataType*)realloc(hp->a,newcapacity * sizeof(HPDataType));
		if (hp->a == NULL)
		{
			perror("realloc fail");
			return;
		}
		hp->a = newnode;
		hp->capacity = newcapacity;
	}
	hp->a[hp->size] = x;
	hp->size++;
	//也可写成：hp->a[hp->size++] = x;
	AdjustUp(hp->a, hp->size - 1);//向上调整
}

                3.4堆的删除

void AdjustDown(HPDataType* a, int n, int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		if (a[child] > a[child+1])//此步的目的是找到最小的
		{
			child++;
		}
		if (a[parent] > a[child])
		{
			sweap(&a[parent], &a[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
void HeapPop(Heap* hp)
{
	assert(hp);
	assert(hp->size > 0);
	sweap(&hp->a[0], &hp->a[hp->size - 1]);//删除顶元素
	hp->size--;
	AdjustDown(hp->a, hp->size, 0);//向下调整
}

        堆的删除不是删除最后一个元素，而是删除首元素！！！

        3.5 取堆顶元素

HPDataType HeapTop(Heap* hp)
{
	assert(hp);
	assert(hp->size > 0);
	return hp->a[0];
}

        3.6 对堆判空

bool HeapEmpty(Heap* hp)
{
	assert(hp);
	return hp->size == 0;
}

        好了，以上便是对堆的全部实现，大家稍微休息片刻，接下来咱们进入堆排序。

四、堆排序

        接下来，咱们来搞堆排序。对于堆排序，大家有没有什么想法：升序是建大堆还是小堆，降序是建小堆还是大堆。对于这个问题，有人肯定会有这样的想法：降序，那不是非大堆莫属，升序，那不是非小堆莫属。非也。

        那么，有什么方法呢？答案为：降序：小堆；升序：大堆。 

        就以降序为例：排降序咱们首先先把根（也就是祖先）扔到最后，之后不在理会它，推选出下一个祖先，重复即可。

        以上，便为实现思路。

        这只是一个大致方向，我们拿这个大致方向去实现肯定会困难重重。那我们面临最大的困难是什么呢？ 答案为：向下调整的使用条件。向下调整使用的前提是什么？左右子树必须是一个堆，才能调整。这个问题说起来不容易，实际做起来也不容易。那么，我们该如何完成呢？如下：

        1.我们想找到最后一个节点的父节点。

        2.将这个小堆进行向下调整。

        3.然后，对其它节点也使用其类似方法。

        这个方法是不是特别巧妙，以“农村包围城市”的思想，悄无声息就完成了这件大事。 妙哉！

        接下来便是推排序代码实现：

void HeapSort(int* a, int n)
{
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(a, n, i);//见小堆
	}
	int end = n - 1;
	while (end)
	{
		sweap(&a[0], &a[end]);
		AdjustDown(a, end, 0);//经行排序
		end--;
	}
}

五、TOP-K 问题

        什么为TOP-K问题呢？以下为大家构建一个场景：

        你在大学里苦学两年，计划在大二的暑假的暑假找一份实习。和你预期一样，一家公司向你发起了面试，对于前面的计算机知识你对答入流，当你以为你能够“黄袍加身”之时，面试官问出了最后一题，我给你一个文件，里面有十万个数据，给我选出最大的十个出来。你当时在心里想：就这。你立马动态开辟了这么大的空间，运用堆排序，立马拿到了结果。面试官喝了口茶，说了句：“太大了。”你以为说的是茶太烫了，想着要不要做点什么的时候，然后面试官缓缓地说：“如果我给你1MB的空间，能不能搞出来，1KB的空间，行不行？”你不由得在心中想：你就是想为难我，当没想到，我重生了（一键三连即可听故事），这个问题早已被我攻克，我可是要站在顶尖的人。于是，你大笔一挥写出的代码震惊到面试官，于是如愿成为实习生。

        本问题已经明确，在很大的数据面前，用极小的内存得到想要的结果。

        具体实现思路如下：在十万数据中得到最大的十个数。我们可先取出十个数，建小堆，和其他数字比，如果有数字比顶元素大，便替换掉顶元素，进入堆，在向下调整，直到对比完。         

        代码实现如下：

void CreateNDate()
{
	// 造数据
	int n = 10000;
	srand(time(0));
	const char* file = "data.txt";
	FILE* fin = fopen(file, "w");
	if (fin == NULL)
	{
		perror("fopen error");
		return;
	}

	for (size_t i = 0; i < n; ++i)
	{
		int x = rand() % 1000000;
		fprintf(fin, "%d\n", x);
	}

	fclose(fin);
}

void PrintTopK(int k)
{
	int k;
	printf("请输入k>:");
	scanf("%d", &k);
	int* kminheap = (int*)malloc(sizeof(int) * k);
	if (kminheap == NULL)
	{
		perror("malloc fail");
		return;
	}
	const char* file = "data.txt";
	FILE* fout = fopen(file, "r");
	if (fout == NULL)
	{
		perror("fopen error");
		return;
	}

	// 读取文件中前k个数
	for (int i = 0; i < k; i++)
	{
		fscanf(fout, "%d", &kminheap[i]);
	}
	// 建K个数的小堆
	for (int i = (k - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(kminheap, k, i);
	}

	// 读取剩下的N-K个数
	int x = 0;
	while (fscanf(fout, "%d", &x) > 0)
	{
		if (x > kminheap[0])
		{
			kminheap[0] = x;
			AdjustDown(kminheap, k, 0);
		}
	}

	printf("最大前%d个数：", k);
	for (int i = 0; i < k; i++)
	{
		printf("%d ", kminheap[i]);
	}
	printf("\n");
}

 六、代码总览

        heap.h

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>

typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}Heap;

void HeapInit(Heap* php);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
bool HeapEmpty(Heap* hp);
//向下调整建堆
void AdjustDown(HPDataType* a, int n, int parent);
void sweap(int* p1, int* p2);

heap.c

#include"heap.h"

void HeapInit(Heap* php)
{
	assert(php);
	php->a = NULL;
	php->capacity = php->size = 0;
}
// 堆的销毁
void HeapDestory(Heap* hp)
{
	assert(hp);
	free(hp->a);
	hp->a = NULL;
	hp->capacity = hp->size = 0;
}
// 堆的插入
void sweap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}
void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[parent] > a[child])
		{
			sweap(&a[parent], &a[child]);//注意：这里一定要传地址，&不要忘记
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}
void HeapPush(Heap* hp, HPDataType x)
{
	assert(hp);
	if (hp->capacity == hp->size)
	{
		int newcapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;
		HPDataType* newnode = (HPDataType*)realloc(hp->a,newcapacity * sizeof(HPDataType));
		if (hp->a == NULL)
		{
			perror("realloc fail");
			return;
		}
		hp->a = newnode;
		hp->capacity = newcapacity;
	}
	hp->a[hp->size] = x;
	hp->size++;
	//也可写成：hp->a[hp->size++] = x;
	AdjustUp(hp->a, hp->size - 1);//向上调整
}
// 堆的删除
void AdjustDown(HPDataType* a, int n, int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		if (a[child] > a[child+1])//此步的目的是找到最小的
		{
			child++;
		}
		if (a[parent] > a[child])
		{
			sweap(&a[parent], &a[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
void HeapPop(Heap* hp)
{
	assert(hp);
	assert(hp->size > 0);
	sweap(&hp->a[0], &hp->a[hp->size - 1]);//删除顶元素
	hp->size--;
	AdjustDown(hp->a, hp->size, 0);//向下调整
}
// 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{
	assert(hp);
	assert(hp->size > 0);
	return hp->a[0];
}
// 堆的数据个数
int HeapSize(Heap* hp)
{
	assert(hp);
	return hp->size;
}
// 堆的判空
bool HeapEmpty(Heap* hp)
{
	assert(hp);
	return hp->size == 0;
}

test.c(推排序和TOP-K问题）

#include"heap.h"


void HeapSort(int* a, int n)
{
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(a, n, i);
	}
	int end = n - 1;
	while (end)
	{
		sweap(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		end--;
	}
}
void CreateNDate()
{
	// 造数据
	int n = 10000;
	srand(time(0));
	const char* file = "data.txt";
	FILE* fin = fopen(file, "w");
	if (fin == NULL)
	{
		perror("fopen error");
		return;
	}

	for (size_t i = 0; i < n; ++i)
	{
		int x = rand() % 1000000;
		fprintf(fin, "%d\n", x);
	}

	fclose(fin);
}

void PrintTopK(int k)
{
	int k;
	printf("请输入k>:");
	scanf("%d", &k);
	int* kminheap = (int*)malloc(sizeof(int) * k);
	if (kminheap == NULL)
	{
		perror("malloc fail");
		return;
	}
	const char* file = "data.txt";
	FILE* fout = fopen(file, "r");
	if (fout == NULL)
	{
		perror("fopen error");
		return;
	}

	// 读取文件中前k个数
	for (int i = 0; i < k; i++)
	{
		fscanf(fout, "%d", &kminheap[i]);
	}
	// 建K个数的小堆
	for (int i = (k - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(kminheap, k, i);
	}

	// 读取剩下的N-K个数
	int x = 0;
	while (fscanf(fout, "%d", &x) > 0)
	{
		if (x > kminheap[0])
		{
			kminheap[0] = x;
			AdjustDown(kminheap, k, 0);
		}
	}

	printf("最大前%d个数：", k);
	for (int i = 0; i < k; i++)
	{
		printf("%d ", kminheap[i]);
	}
	printf("\n");
}

最后

        今天的学习到这里就结束了，我们明天将开始二叉树的学习。到时候再会！

完！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1693772.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

电商公司需不需要建数字档案室呢

电商公司需不需要建数字档案室呢

建立数字档案室对于电商公司来说是非常有必要的。以下是一些原因&#xff1a; 1. 空间节约&#xff1a;数字档案室可以将纸质文件转化为电子文件&#xff0c;节省了大量存储空间。这对于电商公司来说尤为重要&#xff0c;因为他们通常会有大量的订单、客户信息和供应商合同等文…
阅读更多...
Python01：初入Python（Mac）

Python01：初入Python（Mac）

Python环境准备 下载Python&#xff1a;官网https://www.python.org/ 下载PyCharm&#xff1a;官网https://www.jetbrains.com/pycharm/download Python与PyCharm的关系 Python&#xff08;解释器&#xff09;&#xff1a;机器语言—>翻译人员–>翻译成电脑能读懂的 PyC…
阅读更多...
DatePicker日期选择框（antd-design组件库）简单使用

DatePicker日期选择框（antd-design组件库）简单使用

1.DatePicker日期选择框 输入或选择日期的控件。 2.何时使用 当用户需要输入一个日期&#xff0c;可以点击标准输入框&#xff0c;弹出日期面板进行选择。 组件代码来自&#xff1a; 日期选择框 DatePicker - Ant Design 3.本地验证前的准备 参考文章【react项目antd组件-demo:…
阅读更多...
2022蓝桥杯大赛软件类国赛Java大学B组 左移右移 空间换时间+双指针

2022蓝桥杯大赛软件类国赛Java大学B组 左移右移 空间换时间+双指针

import java.util.Scanner;public class Main {static Scanner scnew Scanner(System.in);public static void main(String[] args) {int nsc.nextInt();//数组长度int tsc.nextInt();//操作次数int arr[]new int[n];char arr1[] new char[t];int arr2[] new int[t];int vis…
阅读更多...
金融信贷风控系统设计模式应用之模版方法

金融信贷风控系统设计模式应用之模版方法

背景介绍 风控系统每种场景 如个人消费贷 都需要跑很多规则 规则1 申请人姓名身份证号实名验证规则2 申请人手机号码实名认证规则3 银行卡预留手机号码实名认证规则4 申请人银行卡预留手机号码在网状态检验规则5 申请人银行借记卡有效性核验规则6 户籍地址与身份证号归属地比…
阅读更多...
后量子密码解决方案

后量子密码解决方案

什么是后量子密码学 (PQC)&#xff0c;为什么准备工作如此重要? 量子计算正在迅速发展;用不了多久&#xff0c;量子网络攻击就会成为可能。量子网络攻击将能够在几分钟内瘫痪大型网络。我们今天赖以保护我们的连接和交易的一切都将受到量子计算机的威胁&#xff0c;危及所有密…
阅读更多...
Django中model中的抽象类

Django中model中的抽象类

Django中model中的抽象类 当我们在app中models.py文件中定义model表并执行python manage.py makemigrations和python manage.py migrate后&#xff0c;Django就会在数据库中创建表 但是我们也可以对其默认配置修改&#xff0c;定义model类但是不在数据库中创建 from django.…
阅读更多...
Behind the Code：Polkadot 如何重塑 Web3 未来

Behind the Code：Polkadot 如何重塑 Web3 未来

2024 年 5 月 17 日 Polkadot 生态 Behind the Code 第二季第一集 《创造 Web3 的未来》正式上线。第一集深入探讨了 Polkadot 和 Web3 技术在解决数字身份、数据所有权和去中心化治理方面的巨大潜力。 &#x1f50d; 查看完整视频&#xff1a; https://youtu.be/_gP-M5nUidc?…
阅读更多...
基于Python对评论进行情感分析可视化

基于Python对评论进行情感分析可视化

欢迎大家点赞、收藏、关注、评论啦 &#xff0c;由于篇幅有限&#xff0c;只展示了部分核心代码。 文章目录 一项目简介 二、功能三、系统四. 总结 一项目简介 一、项目背景与意义 在当今数字化时代&#xff0c;用户生成内容&#xff08;UGC&#xff09;如在线评论、社交媒体…
阅读更多...
需求响应+配网重构！含高比例新能源和用户需求响应的配电网重构程序代码！

需求响应+配网重构！含高比例新能源和用户需求响应的配电网重构程序代码！

前言 配电网重构作为配电网优化运行的手段之一&#xff0c;通过改变配电网的拓扑结构&#xff0c;以达到降低网损、改善电压分布、提升系统的可靠性与经济性等目的。近年来&#xff0c;随着全球能源消耗快速增长以及环境的日趋恶化&#xff0c;清洁能源飞速发展&#xff0c;分…
阅读更多...
线性回归模型

线性回归模型

目录 1.概述 2.线性回归模型的定义 3.线性回归模型的优缺点 4.线性回归模型的应用场景 5.线性回归模型的未来展望 6.小结 1.概述 线性回归是一种广泛应用于统计学和机器学习的技术&#xff0c;用于研究两个或多个变量之间的线性关系。在本文中&#xff0c;我们将深入探讨…
阅读更多...
GM Bali，OKLink受邀参与Polygon AggIsland大会

GM Bali，OKLink受邀参与Polygon AggIsland大会

5月16日-17日&#xff0c;OKLink 受到生态合作伙伴 Polygon 的特别邀请&#xff0c;来到巴厘岛参与以 AggIsland 为主题的大会活动并发表演讲&#xff0c;详细介绍 OKLink 为 Polygon 所带来的包括多个浏览器和数据解析等方面的成果&#xff0c;并与 Polygon 一起&#xff0c;对…
阅读更多...
【maven与tomcat配置】如何正确配置maven及tomcat环境变量及运行Java项目 (附图文说明及下载包)

【maven与tomcat配置】如何正确配置maven及tomcat环境变量及运行Java项目 (附图文说明及下载包)

maven及tomcat配置详解 &#x1f354;涉及知识&#x1f964;写在前面&#x1f367;一、maven和tomcat是啥&#xff1f;&#x1f367;二、maven环境变量配置2.1获取maven包2.2创建本地仓库及修改配置A&#xff0e;校验是否安装javaB&#xff0e;创建本地maven存放仓库C&#xff…
阅读更多...
C++vector的简单模拟实现

C++vector的简单模拟实现

文章目录 目录 文章目录 前言 一、vector使用时的注意事项 1.typedef的类型 2.vector不是string 3.vector 4.算法sort 二、vector的实现 1.通过源码进行猜测vector的结构 2.初步vector的构建 2.1 成员变量 2.2成员函数 2.2.1尾插和扩容 2.2.2operator[] 2.2.3 迭代器 2…
阅读更多...
OpenHarmony系统使用gdb调试init

OpenHarmony系统使用gdb调试init

前言 OpenAtom OpenHarmony&#xff08;简称“OpenHarmony”&#xff09;适配新的开发板时&#xff0c;启动流程init大概率会出现问题&#xff0c;其为内核直接拉起的第一个用户态进程&#xff0c;问题定位手段只能依赖代码走读和增加调试打印&#xff0c;初始化过程中系统崩溃…
阅读更多...
单片机设计注意事项

单片机设计注意事项

1.电源线可以30mil走线&#xff0c;信号线可以6mil走线 2.LDO推荐 SGM2019-3.3,RT9013,RT9193,1117-3.3V。 3.单片机VCC要充分滤波后再供电&#xff0c;可以接0.1uf的电容 4.晶振附件不要走其他元件&#xff0c;且放置完单片机后就放置晶振&#xff0c;晶振靠近X1,X2。
阅读更多...
【C++】d1

【C++】d1

关键字&#xff1a; 运行、前缀、输入输出、换行 运行f10 前缀必须项&#xff1a; #include <iostream> using namespace std; 输入/输出&#xff1a; cin >> 输入 cout << 输出 语句通过>>或<<分开 换行 endl或者"\n"
阅读更多...
前端日志收集（monitor-report v1）

前端日志收集（monitor-report v1）

为什么 为什么自己封装而不是使用三方 类似 Sentry 这种比较全面的 因为 Sentry 很大我没安装成功&#xff0c;所有才自己去封装的 为什么使用 可以帮助你简单解决前端收集错误日志、收集当前页面访问量&#xff0c;网站日活跃&#xff0c;页面访问次数&#xff0c;用户行…
阅读更多...
Spring ----＞ IOC

Spring ----＞ IOC

文章目录 一、 Spring 是一个包含众多工具的IoC容器二、 什么是IOC以及好处三、 如何实现loc思想四、Spring提供的实现loC的方法 --- 类注解方法注解4.1 类注解类注解概念介绍类注解的使用 4.2 方法注解Bean 一、 Spring 是一个包含众多工具的IoC容器 场景解析&#xff1a;首先…
阅读更多...
软件设计师备考 | 案例专题之数据库设计 概念与例题

软件设计师备考 | 案例专题之数据库设计 概念与例题

相关概念 关注上图中的两个部分&#xff1a; 概念结构设计 设计E-R图&#xff0c;也即实体-联系图。 工作步骤&#xff1a;选择局部应用、逐一设计分E-R图、E-R图合并。进行合并时&#xff0c;它们之间存在的冲突主要有以下3类&#xff1a; 属性冲突。同一属性可能会存在于…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023