题目
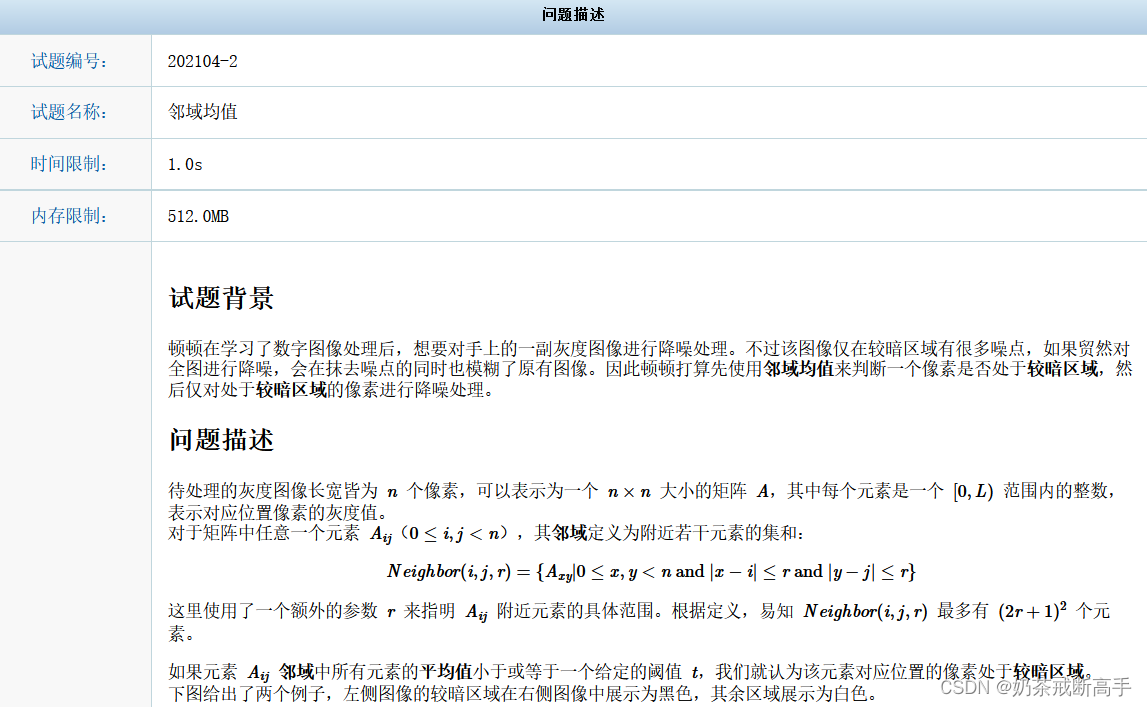
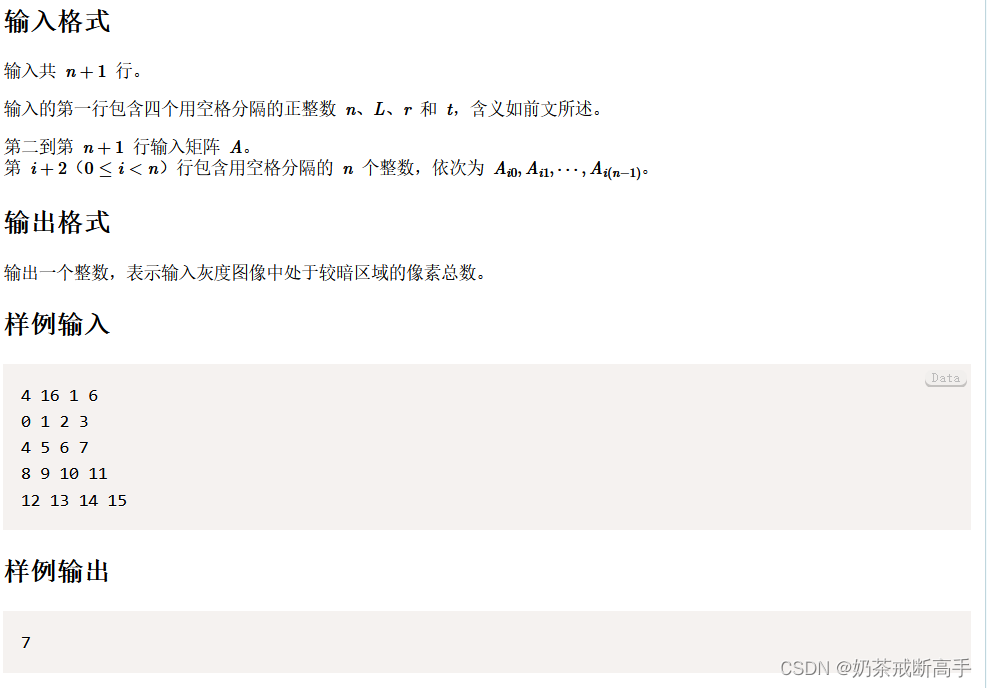
过程
前缀和
定义
假定一个数组，前缀和就是该元素前所有元素和。也就是如果我们舌钉一个数组s为前缀和数组，那么s[3]就是我们原数组前三个元素之和。
优势
降低计算复杂度。
如果我们要求一段区间的和，那么我们用普通数组要从第一个加到最后一个循环一边，但是如果我们知道该数组前缀和之后，我们就只需要去让其末元素前缀和减去初元素前的前缀和就可以了。
就比如我们求下标3-10的数组和，那么我们使用前缀和时就只需要去让是s[10]-s[2] 就可以了。
求法
用递推的方法求s[i]，从头开始求前缀和，之后的前缀和就是其前一个前缀和加上当前元素。
S[i] = S[i-1] + a[i] ;二维前缀和
公式：
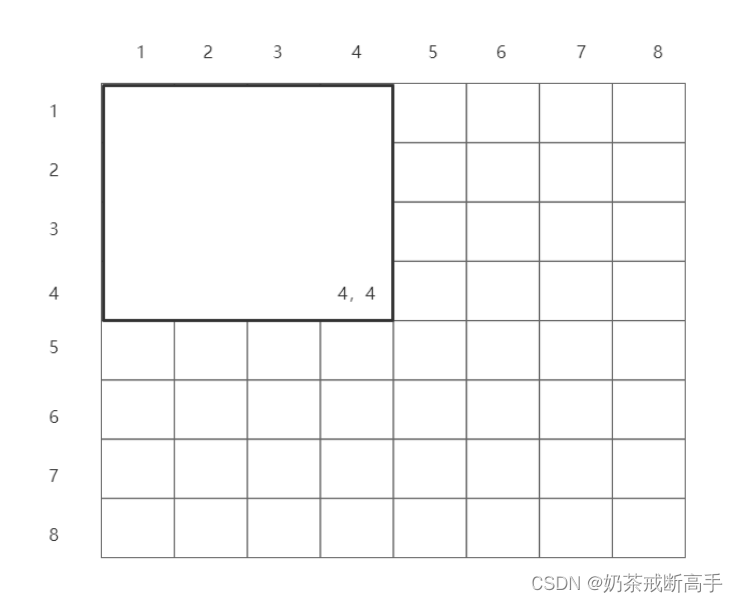
s[i][j] += s[i-1][j] + s[i][j-1] - s[i-1][j-1] 如求（4，4）的前缀和，我们就需要求出这块部分的数值。
s[i][j]=s[4][4]:
s[i][j-1]=s[4][3]:
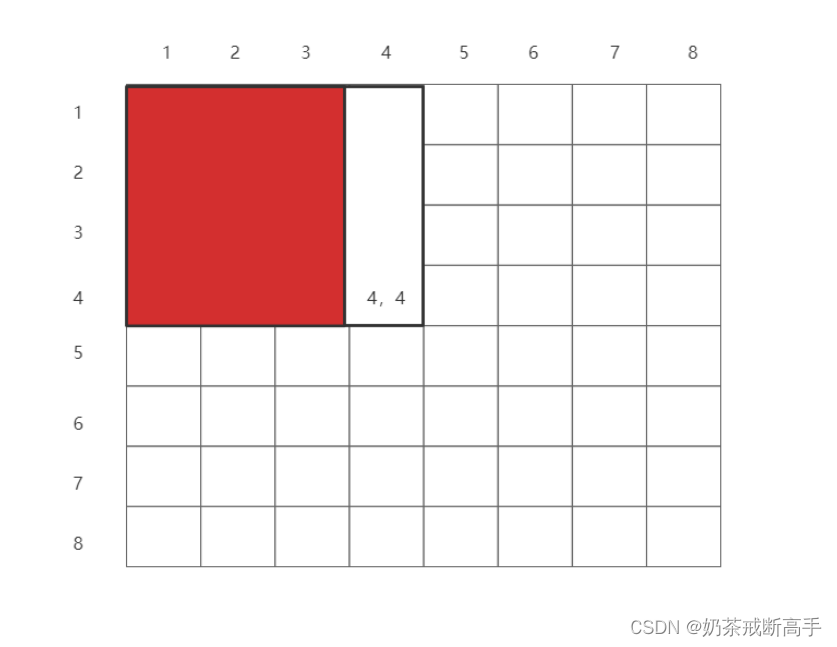s[i-1][j]=s[3][4]:
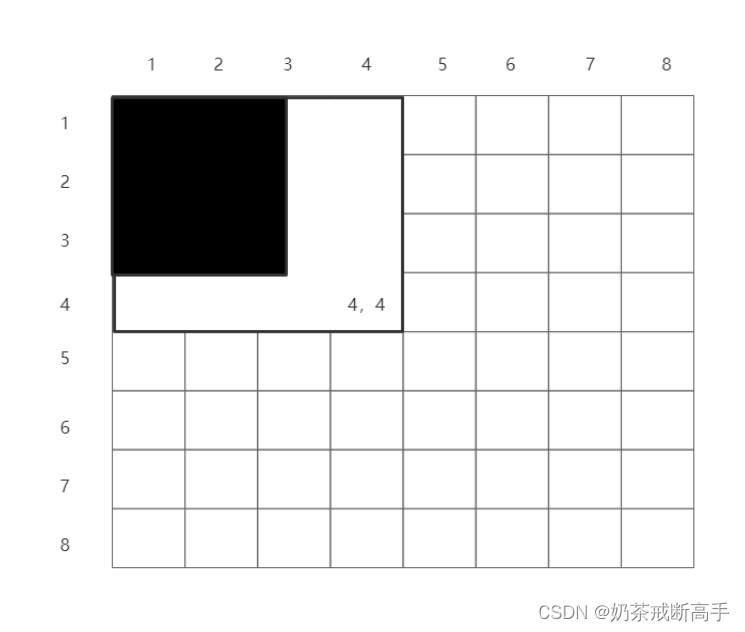
这时我们会发现，如果我们这两个相加的话，我们会相加重叠一部分，那么这个时候我们就需要将中间那一部分减去。s[i-1][j-1]:
这时我们发现还有一格没有算上，只要在这格中填入原数组a[i][j]的数值即可。
思路
采用二维前缀和，设原数组a[N][N]，前缀和数组b[N][N]。
由于矩阵有边界，因此需要对边界范围进行处理：当要下溢出时，将边界设置为1；当要上溢出时，将边界设置为n。
#include<bits/stdc++.h>
using namespace std;
int n,L,r,t;
const int N=1e3+10;
int a[N][N];//输入矩阵
int b[N][N];//前缀和矩阵
int main()
{
cin>>n>>L>>r>>t;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
cin>>a[i][j];
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
b[i][j]=b[i-1][j]+b[i][j-1]-b[i-1][j-1]+a[i][j];
}
}
int num=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
int x1=max(i-r,1);
int x2=min(i+r,n);
int y1=max(j-r,1);
int y2=min(j+r,n);
int n=(y2-y1+1)*(x2-x1+1);
int sum=b[x2][y2]-b[x1-1][y2]-b[x2][y1-1]+b[x1-1][y1-1];
if(sum<=n*t)num++;
}
}
cout<<num;
return 0;
} 结果
