题目列表
3151. 特殊数组 I
3152. 特殊数组 II
3153. 所有数对中数位不同之和
3154. 到达第 K 级台阶的方案数
一、特殊数组I
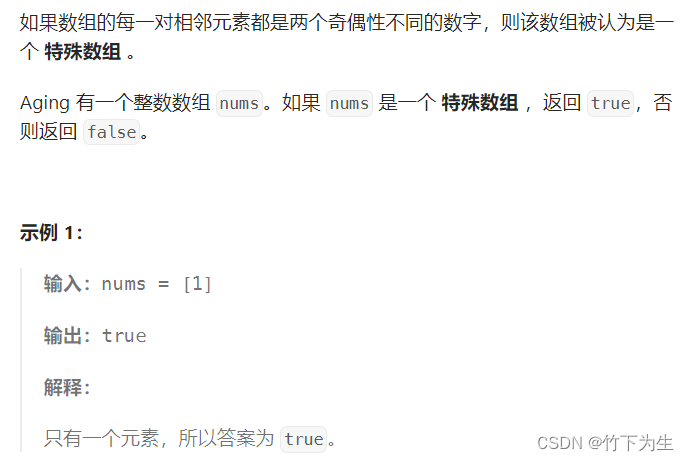
遍历数组,看相邻元素的奇偶性是否相同即可,代码如下
class Solution {
public:
bool isArraySpecial(vector<int>& nums) {
int n = nums.size();
for(int i = 1; i < n; i++){
if((nums[i]+nums[i-1])%2==0) // 奇 + 偶 = 奇
return false;
}
return true;
}
};二、特殊数组II

这一题是第一题的升级版,需要回答所给的询问的区间是否是特殊数组,如果每次询问都是遍历数组来判断是否满足条件,会超时。那么如何做?这里我们可以用前缀和来做,pre[i]用来记录前i个数中的相邻元素奇偶性相同的个数,给定区间[l,r],我们就可以用pre[r]-pre[l]是否等于0来判断该区间内是否有相邻元素奇偶性相同的情况,代码如下
class Solution {
public:
vector<bool> isArraySpecial(vector<int>& nums, vector<vector<int>>& queries) {
int n = nums.size();
vector<int> pre(n);
for(int i=1;i<n;i++){
pre[i] = pre[i-1] + (nums[i]%2==nums[i-1]%2);
}
int m = queries.size();
vector<bool>ans(m);
for(int i=0;i<m;i++){
int l = queries[i][0], r = queries[i][1];
ans[i] = pre[r] == pre[l];
}
return ans;
}
};三、所有数对中数位不同之和

这题就是统计,可以先统计出每一位上0-9出现的次数,然后在去分别计算每一位上数位不同的对数,求和就能得到答案,代码如下
// 两次遍历
class Solution {
public:
long long sumDigitDifferences(vector<int>& nums) {
int n = nums.size();
int m = to_string(nums[0]).size(); // 计算是几位数
vector<vector<int>> cnt(m,vector<int>(10));
// 统计各个数位上0 - 9出现的次数
for(auto x:nums){
int k = 0;
while(x){
cnt[k++][x%10]++;
x/=10;
}
}
long long ans = 0;
for(auto v:cnt){
// 计算每个数位上不同的数对的个数,即使两层for暴力两两组合也能过(一共才10个数进行组合)
long long pre = 0;
for(auto x:v){
ans += x*pre;
pre += x;
}
}
return ans;
}
};
// 一次遍历
class Solution {
public:
long long sumDigitDifferences(vector<int>& nums) {
int n = nums.size();
int m = to_string(nums[0]).size();
vector<vector<int>> cnt(m,vector<int>(10));
long long ans = 0;
for(int i=0;i<n;i++){
int x = nums[i];
for(int k=0;x;x/=10,k++){
ans += i - cnt[k][x%10]++;
}
}
return ans;
}
};四、到达第K级台阶的方案数

这题我们可以用记忆化搜索来做,来暴力查找所有可能的情况。根据题目所给的条件,我们需要记录三个参数,分别为
- i:代表当前数字为几
- j:记录到目前为止操作2执行了多少次,下一次操作二,可以跳2^j
- flag:用来表示上一次操作是操作一/操作二,0 - 操作1,1 - 操作2
递归方程:dfs(i,j,flag) = (flag ? dfs(i-1,j,0) : 0) + dfs(i+(1<<j),j+1,1) + i==k
递归出口:当i>k && j>0时,flag = 0,则无法在往下走了,直接放回0,flag = 1,则可以往回退1个,返回 i-1==k
这题的时间复杂度其实很低,因为操作一不能连续使用,而操作二最多只能进行31次,所以我们的记忆化状态其实很少,具体是多少有兴趣的可以去算一算,下面给出大致的时间复杂度:
1 - m + 1+2^1+...+2^(j-1) = 2^j - m,其中m表示操作1的次数,j表示操作2的次数
如果2^j - m > k,递归退出,m相对于2^j可以直接忽略,所以2^j <= k => j <=logk,而操作一不能连续使用,所以最多也只能使用<=logk次,直接两两暴力组合一下,只有O((logk)^2)
代码如下
class Solution {
public:
int waysToReachStair(int k) {
// dfs(i,j,flag)
// flag = 0 表示上一次操作为操作一
// flag = 1 表示上一次操作为操作二
unordered_map<long long,int> mp;
function<int(int,int,int)>dfs=[&](int i,int j,int flag)->int{
if(i>k && j>0) return flag?i-1==k:0; // 注意:i-1=k&&flag=1的情况
long long mask = flag|j<<1|(long long)i<<32;
if(mp.count(mask)) return mp[mask];
int res = i==k;
res += dfs(i+(1<<j),j+1,1); // 进行操作二
if(flag) res += dfs(i-1,j,0); //进行操作一
return mp[mask]=res;
};
return dfs(1,0,true);
}
};