概念
机器翻译就是用计算机把一种语言翻译成另外一种语言的技术
机器翻译的产生与发展
17 世纪,笛卡尔与莱布尼茨试图用统一的数字代码来编写词典
1930 机器脑
1933 苏联发明家特洛阳斯基用机械方法将一种语言翻译为另一种语言
1946 ENIAC 诞生
1949 机器翻译问题被正式提出
1954 第一个 MT 系统出现
1964 遇到障碍,进入低迷期
1970-1976 开始复苏
1976-1990 繁荣时期
1990-1999 除了双语平行预料,没有其他的发展
1999-now 爆发期
2014 以后出现基于深度学习/神经网络的 MT
机器翻译的要点
正确的机器翻译必须要解决语法与语义歧义
不同类型语言的语言形态不一致
有的词语在不同语言中不能够互通
词汇层的翻译
(1)形态分析:对于原始的句子进行形态分析,对于时态等特殊要素进行标记
(2)词汇翻译
(3)词汇重排序
(4)形态变换
语法层的翻译
语法层的翻译就是将一种语言的语法树映射到另一语言的语法树
e.g.英语 ->日语
V
P
→
V
N
P
c
h
a
n
g
e
t
o
V
P
→
N
P
V
VP \to VNP changeto VP \to NP V
VP→VNPchangetoVP→NPV
P
P
→
P
N
P
c
h
a
n
g
e
t
o
N
P
→
N
P
P
PP \to PNP changeto NP \to NP P
PP→PNPchangetoNP→NPP
三个阶段:句法分析,转换句法树,用目标语法树生成句子
语义层的翻译
基本翻译方法
直接转换法
基于规则的翻译方法
基于中间语言的翻译方法
基于语料库的翻译方法
直接转换法
从源语言的表层出发,直接只换成目标语言译文,必要时进行简单词序调整
基于规则的翻译方法
把翻译这一过程与语法分开,用规则描述语法
翻译过程:
(1)对源语言句子进行词法分析
(2)对源语言句子进行句法/语义分析
(3)结构转换
(4)译文句法结构生成
(5)源语言词汇到译文词汇的转换
(6)译文词法选择与生成
独立分析-独立生成-相关转换
优缺点:可以较好地保持原文的结构,但是规则一般由人工编写,工作量大,对非规范语言无法处理
基于中间语言的翻译方法
源语言解析-比较准确的中间语言-目标语言生成器
基于语料库的翻译方法
基于事例的翻译方法
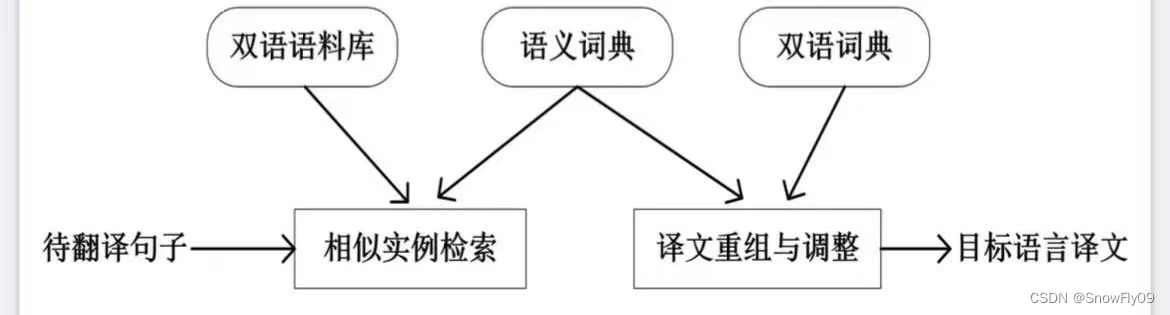
统计机器翻译
获取大量各国语言翻译成英语的文本,然后进行句子对齐
翻译目标:准确度(faithfulness),结构正确/可读性强(fluency)
T
=
arg
max
T
∈
T
a
r
g
e
t
f
a
i
t
h
f
u
l
n
e
s
s
(
T
,
S
)
×
f
l
u
e
n
c
y
(
T
)
T = \arg \max\limits_{T \in Target} faithfulness(T,S) \times fluency(T)
T=argT∈Targetmaxfaithfulness(T,S)×fluency(T)

噪声信道模型
依然与之前语言模型中的贝叶斯类似
将源语言句子
f
=
f
1
f
2
.
.
.
f=f_1f_2...
f=f1f2...翻译到目标语言
e
=
e
1
e
2
e=e_1e_2
e=e1e2,使 P(e|f)最大化
e
^
=
arg
max
e
∈
E
n
g
l
i
s
h
P
(
e
∣
f
)
=
arg
max
e
∈
E
n
g
l
i
s
h
P
(
f
∣
e
)
P
(
e
)
\hat e = \arg \max\limits_{e \in English}P(e|f) = \arg \max\limits_{e \in English}P(f|e)P(e)
e^=arge∈EnglishmaxP(e∣f)=arge∈EnglishmaxP(f∣e)P(e)
此外还需要 decoder 来进行解码
语言模型 p(e)
可以采用 n-gram 或者 PCFG 计算
翻译模型 p(f|e)
对于 IBM Model 1:
(1)选择长度为 m 的句子 f,英文句子长度为 l
(2)选择一到多的对齐方式:A = a1a2…an
(3)对于 f 中的单词 fj,由 e 中相应的对齐词
e
a
j
e_{aj}
eaj生成
red:对齐:一种对齐定义了每个外文词可以由哪个(些)英文词翻译过来
目标式可以表示为:
p
(
f
∣
e
,
m
)
=
∑
a
∈
A
p
(
f
,
a
∣
e
,
m
)
p(f|e,m)=\sum\limits_{a \in A}p(f,a|e,m)
p(f∣e,m)=a∈A∑p(f,a∣e,m)
由链式法则可得:
p
(
f
,
a
∣
e
,
m
)
=
p
(
a
∣
e
,
m
)
p
(
f
∣
a
,
e
,
m
)
p(f,a|e,m) = p(a|e,m)p(f |a,e,m)
p(f,a∣e,m)=p(a∣e,m)p(f∣a,e,m)
对于 p(a|e,m),IBM Model 1 假设所有的对齐方式具有相同的概率:
p
(
a
∣
e
,
m
)
=
1
(
l
+
1
)
m
p(a|e,m) = \frac{1}{(l+1)^m}
p(a∣e,m)=(l+1)m1
对于 p(f|a,e,m),
p
(
f
∣
a
,
e
,
m
)
=
∏
j
=
1
m
t
(
f
j
∣
e
a
j
)
p(f|a,e,m) = \prod\limits_{j=1}^mt(f_j|e_{aj})
p(f∣a,e,m)=j=1∏mt(fj∣eaj)

t(f|e)表示英文词 eaj 翻译成外文词 fj 的概率
故:
p
(
f
∣
e
,
m
)
=
∑
p
(
f
,
a
∣
e
,
m
)
=
∑
a
∈
A
1
(
l
+
1
)
m
∏
j
=
1
m
t
(
f
j
∣
e
a
j
)
p(f|e,m) = \sum p(f,a|e,m) = \sum\limits_{a \in A} \frac{1}{(l+1)^m}\prod\limits_{j=1}^mt(f_j|e_{aj})
p(f∣e,m)=∑p(f,a∣e,m)=a∈A∑(l+1)m1j=1∏mt(fj∣eaj)
根据以上计算式,也可以计算某种对齐方式的概率:
a
∗
arg
max
a
p
(
a
∣
f
,
e
,
m
)
=
arg
max
a
p
(
f
,
a
∣
e
,
m
)
p
(
f
∣
e
,
m
)
a^* \arg \max_ap(a|f,e,m) = \arg \max_a \frac{p(f,a|e,m)}{p(f|e,m)}
a∗argmaxap(a∣f,e,m)=argmaxap(f∣e,m)p(f,a∣e,m)
IBM Model 2:
对于 model 2,引入了对齐时的扭曲系数
q(i|j,l,m)给定 e 和 f 对齐的时候,第 j 个目标语言词汇和第 i 个英文单词对齐的概率
p
(
a
∣
e
,
m
)
=
∏
j
=
1
m
q
(
a
j
∣
j
,
l
,
m
)
p(a|e,m) = \prod\limits_{j=1}^mq(a_j|j,l,m)
p(a∣e,m)=j=1∏mq(aj∣j,l,m)
则
p
(
f
,
a
∣
e
,
m
)
=
∏
j
=
1
m
q
(
a
j
∣
j
,
l
,
m
)
t
(
f
j
∣
e
a
j
)
p(f,a|e,m) = \prod\limits_{j=1}^mq(a_j|j,l,m)t(f_j|e_{aj})
p(f,a∣e,m)=j=1∏mq(aj∣j,l,m)t(fj∣eaj)

IBM model 2 最优对齐:

t 与 q 的计算
已有数据:双语(句子)对齐资料(包含/不包含词对齐信息)
e
(
k
)
,
f
(
k
)
,
a
(
k
)
e^{(k)},f^{(k)},a^{(k)}
e(k),f(k),a(k)
采用极大似然估计法:
t
M
L
(
f
∣
e
)
=
C
o
u
n
t
(
e
,
f
)
C
o
u
n
t
(
e
)
,
t
M
L
(
j
∣
i
,
l
,
m
)
=
C
o
u
n
t
(
j
∣
i
,
l
,
m
)
C
o
u
n
t
(
i
,
l
,
m
)
t_{ML}(f|e) =\frac{Count(e,f)}{Count(e)},t_{ML}(j|i,l,m) = \frac{Count(j|i,l,m)}{Count(i,l,m)}
tML(f∣e)=Count(e)Count(e,f),tML(j∣i,l,m)=Count(i,l,m)Count(j∣i,l,m)

如果不包含词对齐信息:
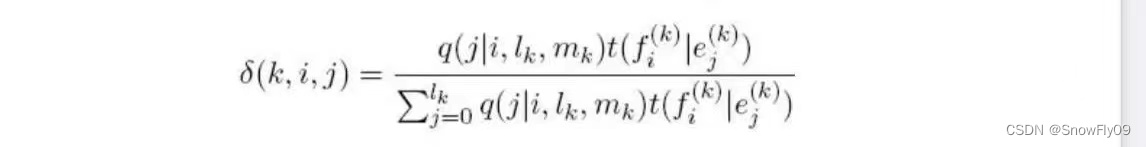

基于短语的翻译
有时候会出现多个词对应一个词的情况,有时候也需要更长的上下文来消除词的歧义,于是推出了基于短语的翻译
基本过程
构建短语对齐词典
基于短语的翻译模型:
(1)词组合成短语
(2)短语翻译
(3)重排序
解码问题
短语对齐词典
输入:句子对齐语料
输出:短语对齐语料
e.g.他将访问中国He will visit China
(他将,He will)(访问中国,visit China)
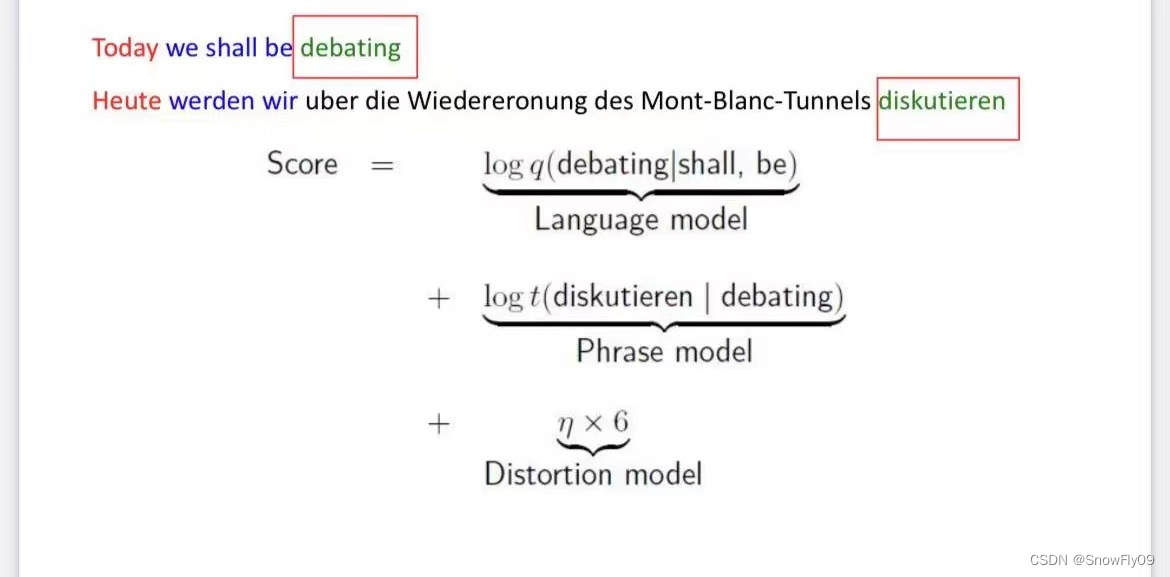
每个互译的短语对(f,e)都有一个表示可能性的分值 g(f,e)
g
(
f
,
e
)
=
log
c
o
u
n
t
(
f
,
e
)
c
o
u
n
t
(
e
)
g(f,e) = \log \frac{count(f,e)}{count(e)}
g(f,e)=logcount(e)count(f,e)
同时使用噪声信道模型依然可以用来表示最优英语翻译:
e
b
e
s
t
=
arg
max
e
p
(
f
∣
e
)
p
L
M
(
e
)
e_{best}=\arg \max_e p(f|e)p_{LM}(e)
ebest=argmaxep(f∣e)pLM(e)
语言模型
一般采用 3-gram:q(w|u,v)
排序模型
可以简化为基于距离的排序:
η
×
∣
s
t
a
r
t
i
−
e
n
d
i
−
1
−
1
∣
\eta \times|start_i-end_{i-1}-1|
η×∣starti−endi−1−1∣
其中
η
\eta
η为扭曲参数,通常为负值
几个概念
p(s,t,e):源句子中 xs 到 xt 的词串可以被翻译为目标语言的词串 e
P:所有短语 p 的集合
y:类似 P,导出,表示一个由有限个短语构成的短语串
e(y):表示由导出 y 确定的翻译
解码问题
求解最优翻译是一个 NP-complete 问题
可能的方案:基于启发式搜索解码算法
状态 q:五元组(e1,e2,b,r,alpha)
e1,e2 表示待翻译短语对应翻译中最后两个英文词
b 为二进制串 ,1 为已经翻译,0 为未翻译
r 表示当前待翻译短语的最后一个词在句子中的位置
alpha 表示该状态的得分
起始
q
0
=
(
/
,
/
,
0
n
,
0
,
0
)
q_0 = (/,/,0^n,0,0)
q0=(/,/,0n,0,0)
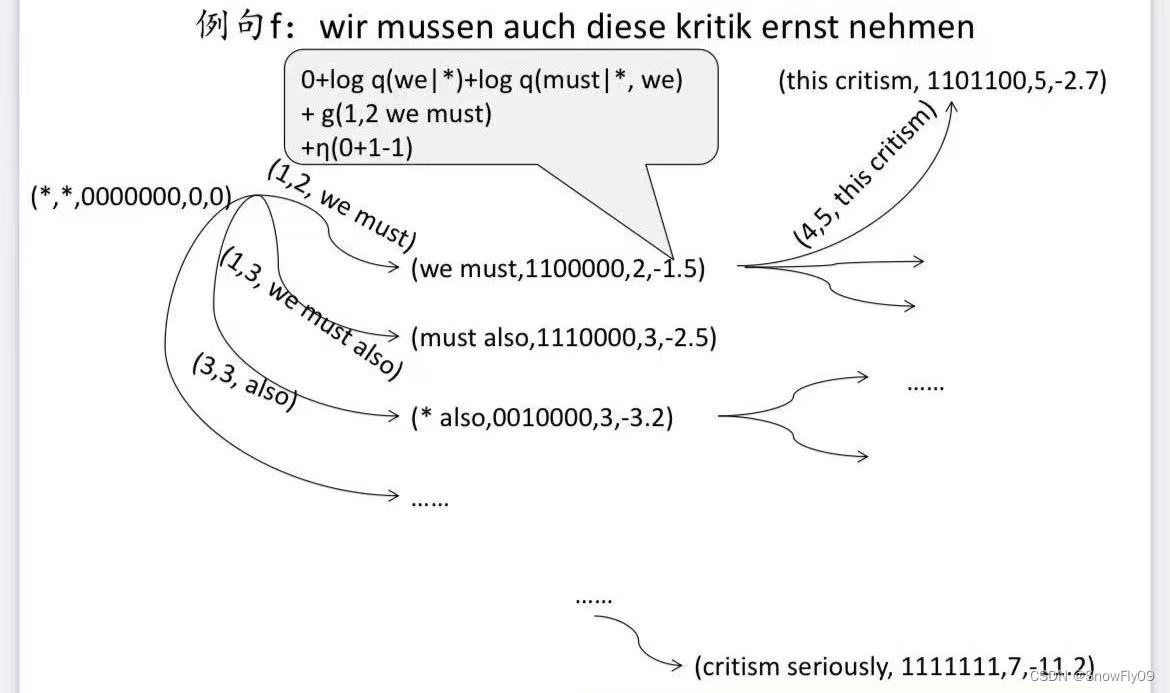
next(q,p) 表示 q 经过短语 p 触发,转移到下一个状态
eq(q,q‘)用来验证两个状态是否相等,只比较前四项值
beam(Q)