数据结构~~二叉树-堆

news2024/11/25 6:49:55

目录

一、基本概念

树的概念

二叉树-堆的概念

二、堆的结构

 三、堆排序

向上调整建堆

向下调整建堆 

 四、TOP-K

五、完整代码

 六、总结

一、基本概念

树的概念

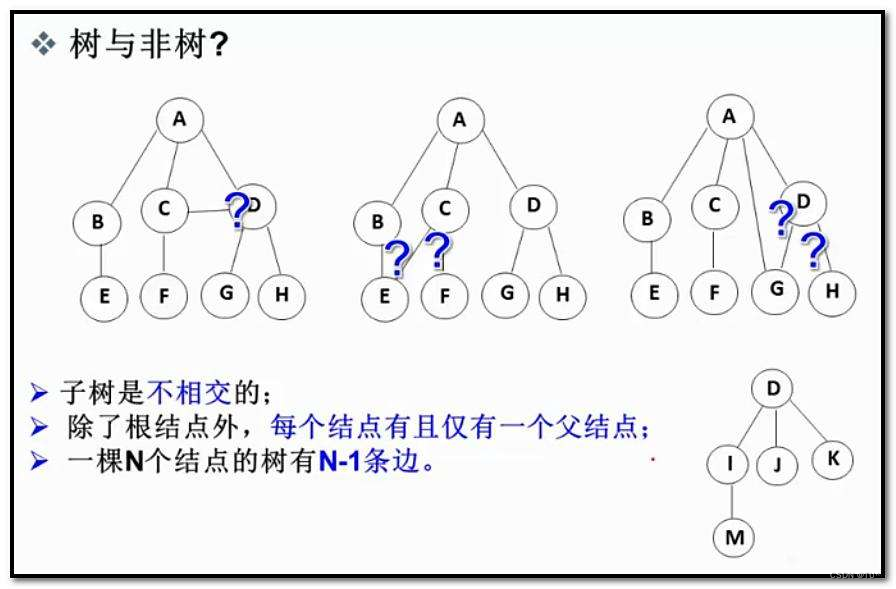
树是一种非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合。把它叫做树是因 为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。 有一个特殊的结点，称为根结点，根节点没有前驱结点 除根节点外，其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm，其中每一个集合Ti(1<=i=M),又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱，可以有0个或多个后继 因此，树是递归定义的。

树形结构中，子树之间不能有交集，否则就不是树形结构

 1.2树的相关概念： 

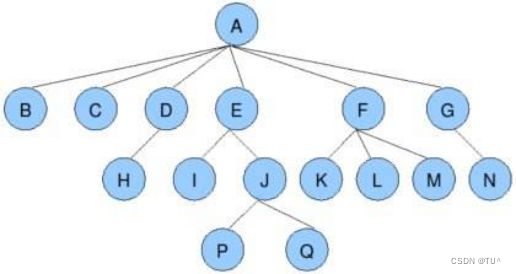
度节点的：一个节点含有的子树的个数称为该节点的度； 如上图：A的为6

叶节点或终端节点：度为0的节点称为叶节点； 如上图：B、C、H、I...等节点为叶节点

非终端节点或分支节点：度不为0的节点； 如上图：D、E、F、G...等节点为分支节点

双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点； 如上图：A是B的父节点

孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点； 如上图：B是A的孩子节点

兄弟节点：具有相同父节点的节点互称为兄弟节点； 如上图：B、C是兄弟节点

树的度：一棵树中，最大的节点的度称为树的度； 如上图：树的度为6

节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推；

树的高度或深度：树中节点的最大层次； 如上图：树的高度为4

堂兄弟节点：双亲在同一层的节点互为堂兄弟；如上图：H、I互为兄弟节点

节点的祖先：从根到该节点所经分支上的所有节点；如上图：A是所有节点的祖先

子孙：以某节点为根的子树中任一节点都称为该节点的子孙。如上图：所有节点都是A的子孙

森林：由m（m>0）棵互不相交的树的集合称为森林；

二叉树-堆的概念

一棵二叉树是结点的一个有限集合，该集合: 1. 或者为空 2. 由一个根节点加上两棵别称为左子树和右子树的二叉树组成

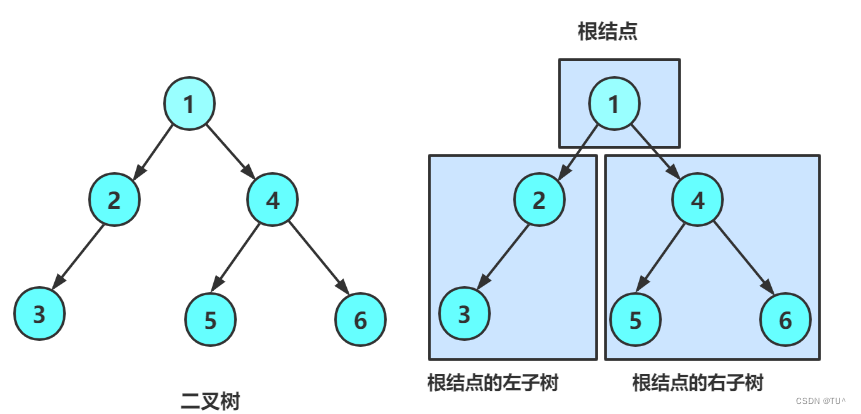
从上图可以看出：1. 二叉树不存在度大于2的结点 2. 二叉树的子树有左右之分，次序不能颠倒，因此二叉树是有序树

对于任意的二叉树都是由以下几种情况复合而成的：

 2.二叉树的性质 

1. 若规定根节点的层数为1，则一棵非空二叉树的第i层上最多有 个结点.

2. 若规定根节点的层数为1，则深度为h的二叉树的最大结点数是 .

3. 对任何一棵二叉树, 如果度为0其叶结点个数为 , 度为2的分支结点个数为 ,则有 ＝ ＋1

4. 若规定根节点的层数为1，具有n个结点的满二叉树的深度，h= . (ps： 是log以2 为底，n+1为对数)

5. 对于具有n个结点的完全二叉树，如果按照从上至下从左至右的数组顺序对所有节点从0开始编号，则对 于序号为i的结点有：

1. 若i>0，i位置节点的双亲序号：(i-1)/2；i=0，i为根节点编号，无双亲节点

2. 若2i+1，左孩子序号：2i+1，2i+1>=n否则无左孩子

3. 若2i+2，右孩子序号：2i+2，2i+2>=n否则无右孩子

3.堆的概念

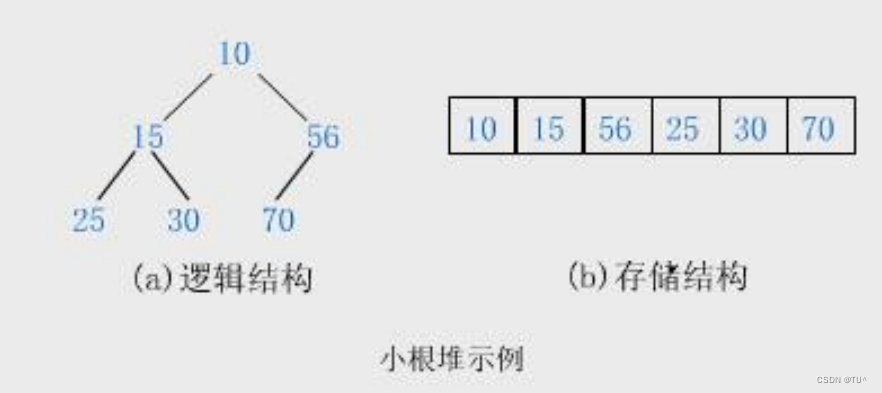
如果有一个关键码的集合K = { ， ， ，…， }，把它的所有元素按完全二叉树的顺序存储方式存储 在一个一维数组中，并满足： 且 = 且 >= ) i = 0，1， 2…，则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。 堆的性质： 堆中某个节点的值总是不大于或不小于其父节点的值； 堆总是一棵完全二叉树。  

二、堆的结构

typedef int HPDateType;
typedef struct Heap
{
	HPDateType* a;  
	int size;
	int capacity;
}HP;

初始化堆

void HeapInit(HP* php)
{
	assert(php);
	php->a = NULL;
	php->capacity = 0;
	php->size = 0;
}

 摧毁堆

void HeapDestroy(HP* php)
{
	assert(php);
	free(php->a);
	php->a = NULL;
	php->capacity = php->size = 0;
}

向上调整

void AdjustUP(HPDateType* a, int child)
{
	int parent = (child - 1) / 2;
	while (child>0)
	{
		if (a[parent] > a[child])
		{
			HPDateType tmp = a[child];
			a[child] = a[parent];
			a[parent] = tmp;

			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

向下调整

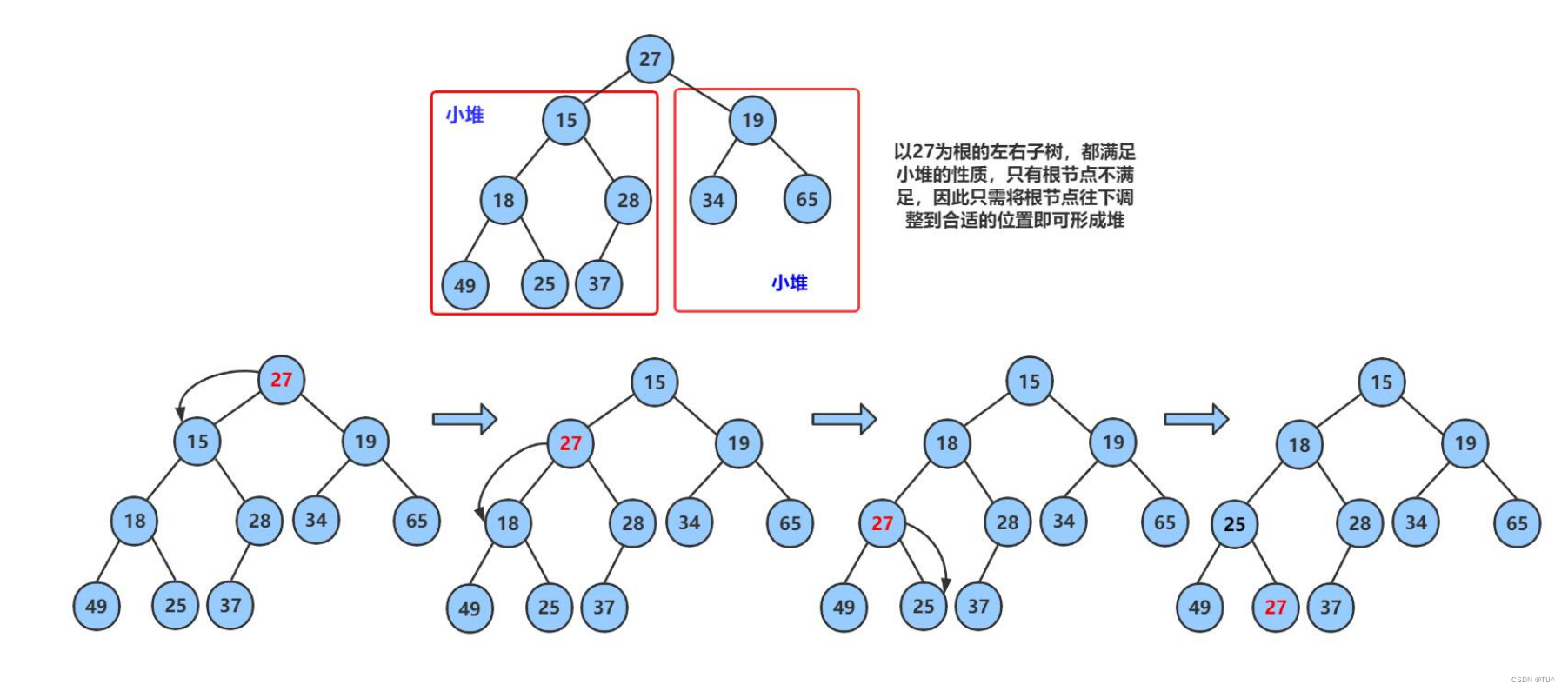
void AdjustDown(int* a,int n,int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		if (child+1 < n && a[child + 1] < a[child])
		{
			child++;
		}
		if (a[child] < a[parent])
		{
			Swap(&a[parent],&a[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

 插入数据

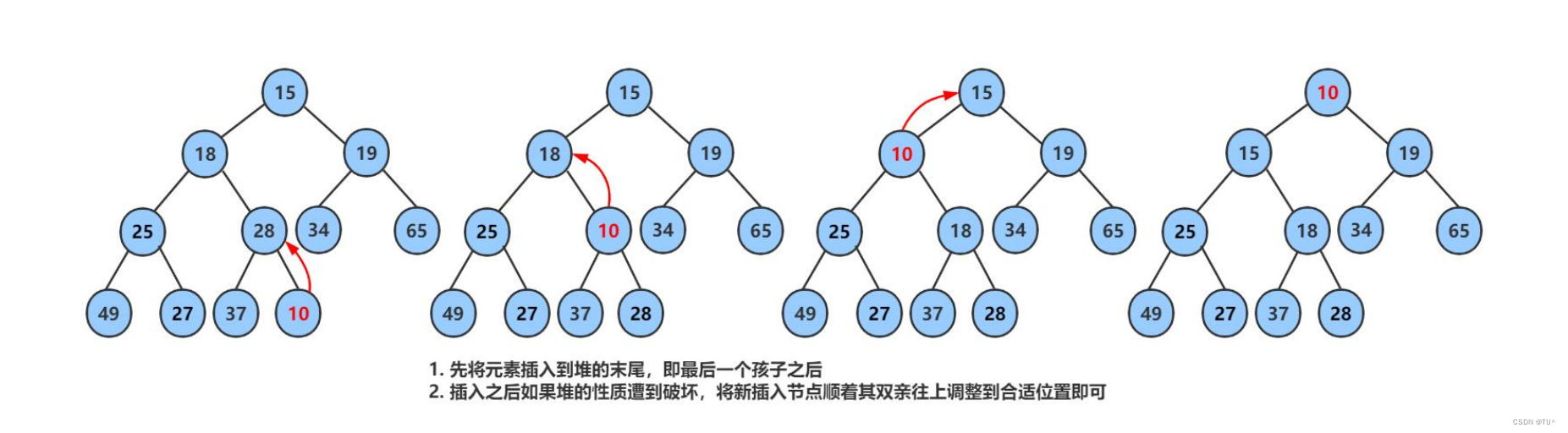
void HeapPush(HP* php, HPDateType x) 
{
	assert(php);
	if (php->size == php->capacity)
	{
		int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDateType* tmp = (HPDateType*)realloc(php->a, newCapacity * sizeof(HPDateType));
		if (tmp == NULL)
		{
			perror("realloc err");
			return;
		}
		php->a = tmp;
		php->capacity = newCapacity;
	}
	php->a[php->size] = x;
	php->size++;
	AdjustUP(php->a,php->size-1);
}

删除数据

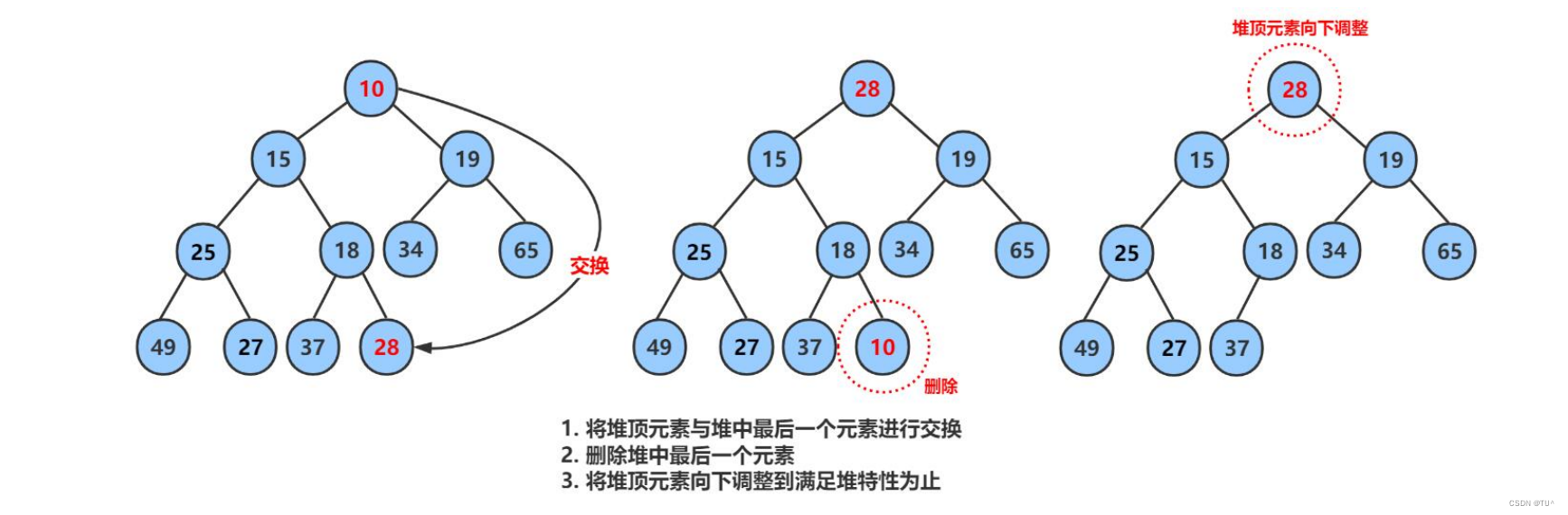
void HeapPop(HP* php)
{
	assert(php);
	assert(!HeapEmpty(php));
	Swap(&php->a[0], &php->a[php->size-1]);
	php->size--;
	AdjustDown(php->a,php->size,0);

}

获取堆顶元素 

HPDateType HeapTop(HP* php)
{
	assert(php);
	assert(!HeapEmpty(php));
	return php->a[0];
}

判断堆是否为空

bool HeapEmpty(HP* php)
{
	assert(php);
	return php->size == 0;
}

获取堆的长度 

int HeapSize(HP* php)
{
	assert(php);
	assert(!HeapEmpty(php));
	return php->size;
}

 三、堆排序

向上调整建堆

1.升序建大堆

// 对数组进行堆排序
void AdjustUP(HPDateType* a, int child)
{
	int parent = (child - 1) / 2;
	while (child>0)
	{
		if (a[parent] > a[child])
		{
			HPDateType tmp = a[child];
			a[child] = a[parent];
			a[parent] = tmp;

			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}
void HeapSort(int* a, int n)
{
	//建堆小堆
	for (int i = 1; i < n; i++)
	{
		AdjustUP(a, i);
	}
	int end = n - 1;
	//排序升序
	while (end > 0)
	{
		Swap(&a[0],&a[end]);
		AdjustDown(a, end, 0);
		end--;
	}
}
void test()
{
	int arr[] = { 58,5,28,95,62,65,89,85,61,88,90,78,86,87 ,236,1 };
	HeapSort(arr, sizeof(arr) / sizeof(arr[0]));
	for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++)
	{
		printf("%d ",arr[i]);
	}
}
int main()
{
   test();
}

建堆后：

排序后 ：

 2.降序建小堆

// 对数组进行堆排序
void AdjustDown(int* a,int n,int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		if (child+1 < n && a[child + 1] < a[child])
		{                             //控制大小堆
			child++;
		}
		if (a[child] < a[parent])
		{         //控制大小堆
			Swap(&a[parent],&a[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
void AdjustUP(HPDateType* a, int child)
{
	int parent = (child - 1) / 2;
	while (child>0)
	{
		if (a[parent] > a[child])
		{       //控制建大小堆
			HPDateType tmp = a[child];
			a[child] = a[parent];
			a[parent] = tmp;

			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}
void HeapSort(int* a, int n)
{
	for (int i = 1; i < n; i++)
	{
		AdjustUP(a, i);
	}
	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		end--;
	}
}
void test()
{
	int arr[] = { 58,5,28,95,62,65,89,85,61,88,90,78,86,87 ,236,1 };
	HeapSort(arr, sizeof(arr) / sizeof(arr[0]));
	for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++)
	{
		printf("%d ",arr[i]);
	}
}
int main()
{
   test();
}

建堆后 :

排序后： 

向下调整建堆 

void AdjustDown(int* a,int n,int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		if (child+1 < n && a[child + 1] > a[child])
		{                             //控制大小堆
			child++;
		}
		if (a[child] > a[parent])
		{         //控制大小堆
			Swap(&a[parent],&a[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
void HeapSort(int* a, int n)
{
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(a, n, i);
	}
	int end = n - 1;
	while (end > 0) //n*logn
	{
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		end--;
	}
}
void test()
{
	int arr[] = { 58,5,28,95,62,65,89,85,61,88,90,78,86,87 ,236,1 };
	HeapSort(arr, sizeof(arr) / sizeof(arr[0]));
	for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++)
	{
		printf("%d ", arr[i]);
	}
}
int main()
{ 
    test();
}

建堆：

排序后：

向上调整建堆和向下调整建堆的时间复杂度有所不同。

向上调整建堆的时间复杂度为。O(N*logN)

向下调整建堆的时间复杂度为。O(N)

在实际应用中，通常采用向下调整建堆的方式，因为它的时间复杂度较低。但在某些特定情况下，向上调整建堆也可能会被使用。

 四、TOP-K

思路：

topk 问题是指在一组数据中，找出前 k 个最大或最小的元素。以下是解决 topk 问题的思路和算法： 

建立最小堆或最大堆：使用堆数据结构来解决 topk 问题。可以先建立一个大小为 k 的最小堆或最大堆，然后依次将剩余的元素与堆顶元素进行比较。如果元素大于或小于堆顶元素，则将其替换堆顶元素，并重新调整堆。最后，堆中的元素就是前 k 个最大或最小的元素。这种方法的时间复杂度为O(NlogK)

当N远比K大是时间复杂度为O(N)

在实际应用中，需要根据具体情况选择合适的算法来解决 topk 问题。如果数据量较小，可以使用简单的排序算法或堆算法

typedef int HPDateType;
void Swap(HPDateType* p1, HPDateType* p2)
{
	HPDateType tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}
//向下调整
void AdjustDown(int* a, int n, int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		if (child + 1 < n && a[child + 1] < a[child])
		{                             //控制大小堆
			child++;
		}
		if (a[child] < a[parent])
		{         //控制大小堆
			Swap(&a[parent], &a[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
void CreateNDate()
{
	// 造数据
	int n = 10000;
	srand(time(0));
	const char* file = "data.txt";
	FILE* fin = fopen(file, "w");
	if (fin == NULL)
	{
		perror("fopen error");
		return;
	}

	for (size_t i = 0; i < n; ++i)
	{
		int x = (rand()+i) % 1000000;
		fprintf(fin, "%d\n", x);
	}

	fclose(fin);
}

void PrintTopK()
{
	int k = 0;
	printf("请输入k的值:");
	scanf("%d", &k);
	int* kminheap = (int*)malloc(sizeof(int) * k);
	if (kminheap == NULL)
	{
		perror("malloc file");
		return;
	}      
	const char* file = "data.txt";
	FILE* fout = fopen(file, "r");
	if (fout == NULL)
	{
		perror("fopen error");
		return;
	}
	for (int i = 0; i < k; i++)  //写前k个数据
	{
		fscanf(fout,"%d", &kminheap[i]);
	}
	           //最后的结点的根
	for (int i = (k - 1 - 1) / 2; i >= 0; i--)  //建堆
	{
		AdjustDown(kminheap,k,i);
	}
	int x = 0;
	while (fscanf(fout,"%d", &x) > 0)
	{
		if (x > kminheap[0])
		{
			kminheap[0] = x;
			AdjustDown(kminheap,k,0);
		}
	}
	printf("最大的前k个是：");
	for (int i = 0; i < k; i++)
	{
		printf("%d ",kminheap[i]);
	}
}
int main()
{
    CreateNDate();
	PrintTopK();
}

void CreateNDate()在这个函数生成完一百万个数据时可以在手动添加最大数据，检查代码是否正确

五、完整代码

Heap.h

#include<assert.h>
#include<stdbool.h>
typedef int HPDateType;
typedef struct Heap
{
	HPDateType* a;
	int size;
	int capacity;
}HP;


void HeapInit(HP* php);//初始化堆
void HeapDestroy(HP* php);//摧毁堆

void HeapPush(HP* php,HPDateType x);//插入堆
void HeapPop(HP* php);//删除堆

HPDateType HeapTop(HP* php);//获取堆顶的元素
bool HeapEmpty(HP* php);//堆是否为空
int HeapSize(HP* php);//堆的长度

void AdjustDown(int* a, int n, int parent);//向下调整
void AdjustUP(HPDateType* a, int child);//向上调整

Heap.c 

#include"Heap.h"

void HeapInit(HP* php)
{
	assert(php);
	php->a = NULL;
	php->capacity = 0;
	php->size = 0;
}
void Swap(HPDateType* p1, HPDateType* p2)
{
	HPDateType tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}
void HeapDestroy(HP* php)
{
	assert(php);
	free(php->a);
	php->a = NULL;
	php->capacity = php->size = 0;
}
void AdjustDown(int* a,int n,int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		if (child+1 < n && a[child + 1] < a[child])
		{
			child++;
		}
		if (a[child] < a[parent])
		{
			Swap(&a[parent],&a[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
void AdjustUP(HPDateType* a, int child)
{
	int parent = (child - 1) / 2;
	while (child>0)
	{
		if (a[parent] > a[child])
		{
			HPDateType tmp = a[child];
			a[child] = a[parent];
			a[parent] = tmp;

			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}
void HeapPush(HP* php, HPDateType x) 
{
	assert(php);
	if (php->size == php->capacity)
	{
		int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDateType* tmp = (HPDateType*)realloc(php->a, newCapacity * sizeof(HPDateType));
		if (tmp == NULL)
		{
			perror("realloc err");
			return;
		}
		php->a = tmp;
		php->capacity = newCapacity;
	}
	php->a[php->size] = x;
	php->size++;
	AdjustUP(php->a,php->size-1);
}
void HeapPop(HP* php)
{
	assert(php);
	assert(!HeapEmpty(php));
	Swap(&php->a[0], &php->a[php->size-1]);
	php->size--;
	AdjustDown(php->a,php->size,0);

}
HPDateType HeapTop(HP* php)
{
	assert(php);
	assert(!HeapEmpty(php));
	return php->a[0];
}
bool HeapEmpty(HP* php)
{
	assert(php);
	return php->size == 0;
}
int HeapSize(HP* php)
{
	assert(php);
	assert(!HeapEmpty(php));
	return php->size;
}

 六、总结

二叉树堆是一种特殊的二叉树，它具有以下性质：

1. 堆中某个节点的值总是不大于或不小于其父节点的值：如果父节点的值大于子节点的值，那么这是一个大顶堆；如果父节点的值小于子节点的值，那么这是一个小顶堆。

2. 堆总是一棵完全二叉树：即除了最后一层可能有部分节点空缺外，其他层的节点都是满的。

二叉树堆可以使用数组来存储，通过维护节点的父子关系和堆的性质，可以实现堆的基本操作，如插入、删除和排序等。常见的堆操作包括：

1. 建堆：将一个数组构建成堆。

2. 堆调整：在插入或删除节点后，对堆进行调整，以保持堆的性质。

3. 堆排序：利用堆的性质进行排序。

二叉树堆在很多领域都有广泛的应用，例如：

1. 优先队列：可以用于实现优先队列，按照优先级对元素进行排序和访问。

2. 数据筛选：从大量数据中快速筛选出前个最大或最小的元素。

3. 图的遍历：在某些图算法中，可以使用堆来优化遍历过程。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1690621.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

探索Python编程乐趣：制作气泡反弹小游戏

探索Python编程乐趣：制作气泡反弹小游戏

新书上架~&#x1f447;全国包邮奥~ python实用小工具开发教程http://pythontoolsteach.com/3 欢迎关注我&#x1f446;&#xff0c;收藏下次不迷路┗|&#xff40;O′|┛ 嗷~~ 目录 一、引言&#xff1a;Python编程的轻松入门 二、游戏实现原理&#xff1a;气泡反弹的逻辑 …
阅读更多...
DFSBFS、827. 最大人工岛、leetcode

DFSBFS、827. 最大人工岛、leetcode

DFS&#xff08;深度优先搜索&#xff09;与BFS&#xff08;广度优先搜索&#xff09;作为图论中的两大主流方法&#xff0c;在图相关题目解题中应用较多。 题目链接及描述 827. 最大人工岛 - 力扣&#xff08;LeetCode&#xff09; 做这道题目时&#xff0c;自己想的是首先遍…
阅读更多...
IDEA中一些常见操作【持续更新】

IDEA中一些常见操作【持续更新】

文章目录 前言善用debugidea中debug按钮不显示自动定位文件【始终选择打开的文件】idea注释不顶格【不在行首】快速定位类的位置【找文件非常快】创建文件添加作者及时间信息快速跳转到文件顶端 底端 前言 因为这些操作偶尔操作一次&#xff0c;不用刻意记忆&#xff0c;有个印…
阅读更多...
基于多源数据的微服务系统失败测试用例诊断

基于多源数据的微服务系统失败测试用例诊断

简介 本文介绍由南开大学、华为云及清华大学共同合作的论文:基于多源数据的微服务系统失败测试用例诊断。该论文已被FSE 2024&#xff08;The ACM International Conference on the Foundations of Software Engineering&#xff09; 会议录用&#xff0c;论文标题为: Fault D…
阅读更多...
MVCC相关

MVCC相关

文章目录 前情要点基于什么引擎并发事务产生的问题不可重复读和幻读区别Next-Key Lock的示例解决并发事务采用的隔离级别当前读(Current Read)快照读(Snapshot Read)参考 MVCC定义表里面的隐藏字段由db_roll_ptr串成的版本链ReadView可见性算法mvcc的可见性算法为什么要以提交的…
阅读更多...
【哈希映射 字符串 乘法原理】2227. 加密解密字符串

【哈希映射 字符串 乘法原理】2227. 加密解密字符串

本文涉及知识点 哈希映射 字符串 乘法原理 LeetCode 2227. 加密解密字符串 给你一个字符数组 keys &#xff0c;由若干 互不相同 的字符组成。还有一个字符串数组 values &#xff0c;内含若干长度为 2 的字符串。另给你一个字符串数组 dictionary &#xff0c;包含解密后所…
阅读更多...
2024年收集搜索引擎蜘蛛大全以及浏览器模拟蜘蛛方法

2024年收集搜索引擎蜘蛛大全以及浏览器模拟蜘蛛方法

对于做SEOer来说经常和搜索引擎蜘蛛打交道&#xff0c;下面整理收集了最全的搜索引擎蜘蛛大全。供有需要的朋友使用&#xff0c;建议收藏。 搜索引擎蜘蛛大全 "TencentTraveler", "Baiduspider", "BaiduGame", "bingbot",//必应蜘蛛…
阅读更多...
深入浅出递归算法

深入浅出递归算法

文章目录 递归思想递归的题目1.汉诺塔问题问题分析代码展示 2.合并两个有序链表问题分析代码展示 3.反转链表问题分析代码展示 4.两两交换 链表中的节点问题分析代码展示 总结 递归思想 递归就是将一个很大的问题拆分成子问题&#xff0c;然后再将子问题继续拆分&#xff0c;拆…
阅读更多...
安全设计 | Microsoft 威胁建模工具Threat Modeling Tool安装及使用详解（文末附样例）

安全设计 | Microsoft 威胁建模工具Threat Modeling Tool安装及使用详解（文末附样例）

1. 概览 微软威胁建模工具&#xff08;Threat Modeling Tool&#xff09;是 Microsoft 安全开发生命周期 (SDL&#xff0c;Security Develop LifeCycle) 的核心要素。 当潜在安全问题处于无需花费过多成本即可相对容易解决的阶段&#xff0c;软件架构师可以使用威胁建模工具提…
阅读更多...
C语言 | Leetcode C语言题解之第109题有序链表转换二叉搜索树

C语言 | Leetcode C语言题解之第109题有序链表转换二叉搜索树

题目&#xff1a; 题解&#xff1a; int getLength(struct ListNode* head) {int ret 0;while (head ! NULL) {ret, head head->next;}return ret; }struct TreeNode* buildTree(struct ListNode** head, int left, int right) {if (left > right) {return NULL;}int …
阅读更多...
力扣刷题---409. 最长回文串【简单】

力扣刷题---409. 最长回文串【简单】

题目描述 给定一个包含大写字母和小写字母的字符串 s &#xff0c;返回 通过这些字母构造成的 最长的回文串 。 在构造过程中&#xff0c;请注意 区分大小写 。比如 “Aa” 不能当做一个回文字符串。 示例 1: 输入:s “abccccdd” 输出:7 解释: 我们可以构造的最长的回文串…
阅读更多...
分享：大数据风险检测报告,哪里查询比较好?

分享：大数据风险检测报告,哪里查询比较好?

随着大数据技术的发展&#xff0c;逐渐被运用到各个领域&#xff0c;基于大数据技术的个人风险检测也就是我们常说的大数据报告在金融环境中运用的十分普遍&#xff0c;那大数据风险检测报告哪里查询比较好呢?本文就为大家简单介绍一下。 大数据风险检测报告查询能查到什么? …
阅读更多...
Leetcode刷题笔记3

Leetcode刷题笔记3

18. 四数之和 18. 四数之和 - 力扣&#xff08;LeetCode&#xff09; 给你一个由 n 个整数组成的数组 nums &#xff0c;和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] &#xff08;若两个四元组元素一一对应&…
阅读更多...
骨位深间距小模具镶件如何走水路？3D打印让一切简单

骨位深间距小模具镶件如何走水路？3D打印让一切简单

在模具制造领域&#xff0c;骨位深且间距小的模具镶件由于结构复杂&#xff0c;传统加工方法难以制造出符合要求的冷却水路&#xff0c;导致模具在注塑过程中容易产生热量积聚&#xff0c;进而引发烫伤、缩孔等不良。然而&#xff0c;随着3D打印技术的飞速发展&#xff0c;这些…
阅读更多...
爬虫逆向实例小记——某数据知识管理网站-DES-ECB模式

爬虫逆向实例小记——某数据知识管理网站-DES-ECB模式

aHR0cHM6Ly9rZC5uc2ZjLmNuL2ZpbmFsUHJvamVjdEluaXQ 注意&#xff1a;本文是逆向部分比较少&#xff0c;主要为了流程走通&#xff0c;限于代码搬运工。 第一步:分析页面 此网站经过请求响应&#xff0c;可以看出响应内容为加密内容。 第二步&#xff1a;判断加密类型 在XHR …
阅读更多...
【Linux】从零开始认识进程间通信 —— 管道

【Linux】从零开始认识进程间通信 —— 管道

送给大家一句话&#xff1a; 人要成长&#xff0c;必有原因&#xff0c;背后的努力与积累一定数倍于普通人。所以&#xff0c;关键还在于自己。 – 杨绛 从零开始认识进程间通信 1 为什么要进程间通信2 进程如何通信3 进程通信的常见方式4 管道4.1 什么是管道4.2 管道通信的系…
阅读更多...
postgresql insert on conflict 不存在则插入，存在则更新

postgresql insert on conflict 不存在则插入，存在则更新

向一张表执行插入动作&#xff0c;如果插入的字段数据已存在&#xff0c;则执行更新操作&#xff0c;不存在则进行插入操作。 1、创建一张表 CREATE TABLE "user_info" ( "id" int2 NOT NULL, "name" varchar(20) COLLATE "pg_catalog&quo…
阅读更多...
近邻算法详细

近邻算法详细

近邻算法&#xff0c;特别是K-近邻算法&#xff08;K-Nearest Neighbors, KNN&#xff09;&#xff0c;是一种基于实例的学习方法&#xff0c;广泛应用于分类和回归分析任务。下面是K-近邻算法的详细说明&#xff1a; 基本概念 K-近邻算法的核心思想是“物以类聚”&#xff0…
阅读更多...
基于transformers框架实践Bert系列1--分类器（情感分类）

基于transformers框架实践Bert系列1--分类器（情感分类）

本系列用于Bert模型实践实际场景&#xff0c;分别包括分类器、命名实体识别、选择题、文本摘要等等。&#xff08;关于Bert的结构和详细这里就不做讲解&#xff0c;但了解Bert的基本结构是做实践的基础&#xff0c;因此看本系列之前&#xff0c;最好了解一下transformers和Bert…
阅读更多...
node版本管理nvm详细教程

node版本管理nvm详细教程

安装 nvm 之前先清理node相关的所有配置&#xff0c;如环境变量、.npmrc文件、node_cache、node_global 等 一、下载nvm 任选一处下载即可 官网&#xff1a;Releases coreybutler/nvm-windows (github.com) 码云&#xff1a;nvm下载仓库: nvm下载仓库 百度网盘&#xff1…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023