DFSBFS、827. 最大人工岛、leetcode

news2024/10/5 15:31:50

DFS（深度优先搜索）与BFS（广度优先搜索）作为图论中的两大主流方法，在图相关题目解题中应用较多。

题目链接及描述

827. 最大人工岛 - 力扣（LeetCode）

做这道题目时，自己想的是首先遍历一遍找到，每个陆地的面积，并且使用一个map存储，key为陆地中具体的坐标对（i，j），value为对应陆地的面积。在第一遍遍历完毕后构建出网格中各个坐标所对应的陆地面积。随后进行第二遍遍历，找到网格中值为0的坐标，并计算其上、下、左、右四个方向所对应的陆地的面积：area1, area2, area3, area4。最终计算出网格为0的为止将其替换为1后所对应的最大陆地面积为area1 + area2 + area3 + area4 + 1。

但是构建map过程中遇到问题，key不知如何选择合适，key如果选择为对应的坐标对(i，j)则无法表示，随后思考如何将(i，j)坐标对映射为1个值作为key。但奈何自己太菜想不到。后来参考题解的一种实现思路。构建标记为mark由2起始，每次遍历到一个陆地，将此陆地所对应坐标对的值全部设置为mark，遍历完一个陆地后，在map中存储此mark对应的陆地面积，并且将mark++，最终第一次遍历后构建效果如下所示：

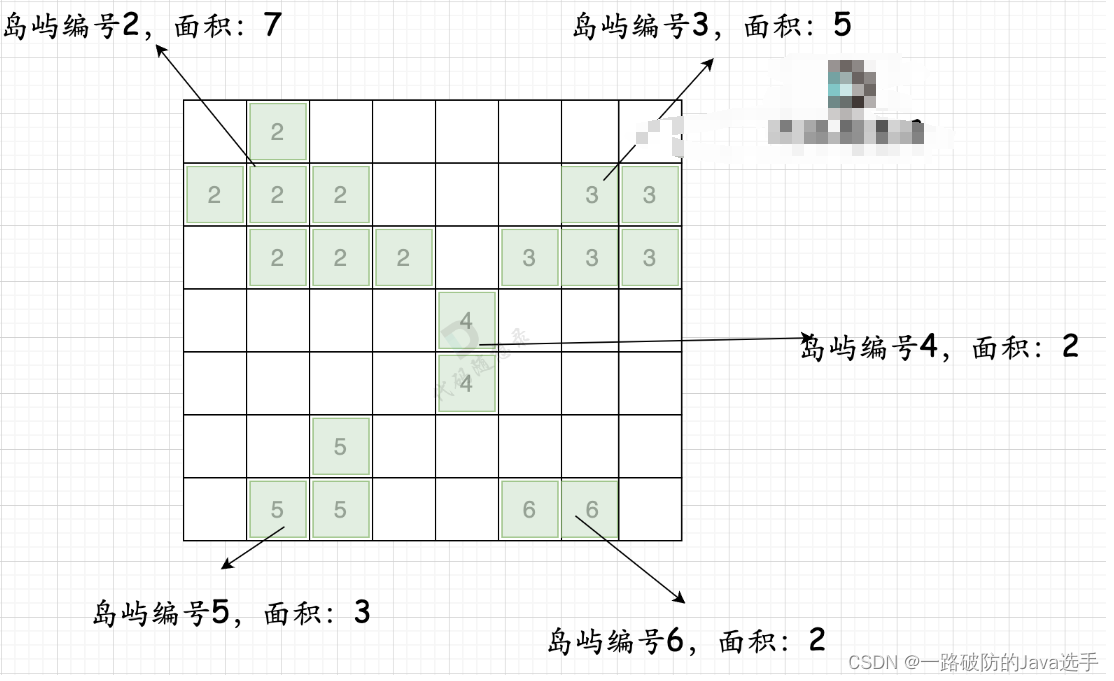
第一次遍历完毕后，进行第二次遍历，寻找网格中坐标值为0的坐标，并找到上下左右四个方向所对应的岛屿面积 + 1即为将此坐标由0变为1所对应的岛屿面积。

代码编写

class Solution {
    public boolean[][] visited;
    public int m, n;
    public int[][] grid;
    public Map<Integer, Integer> map;
    public int[][] idx = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
    public int largestIsland(int[][] grid) {
        this.grid = grid;
        this.m = grid.length; n = grid[0].length;
        visited = new boolean[m][n];
        this.map = new HashMap<>();
        int mark = 2;   // 标记
        boolean flag = true;    // 标记所有位置是否全为1，此时全为陆地
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(grid[i][j] == 0) flag = false;
                if(grid[i][j] == 1 && !visited[i][j]){
                    int ans = dfs(i, j, mark);
                    map.put(mark++, ans);
                }
            }
        }
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                System.out.print(grid[i][j] + " ");
            }
            System.out.println();
        }
        if(flag)    return m * n;
        int ans = 0;
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(grid[i][j] != 0)    continue;
                ans = Math.max(ans, getAroundMaxArea(i, j) + 1);        
            }
        }
        return ans;
    }
    public int getAroundMaxArea(int i, int j){
        int ans = 0;
        Set<Integer> set = new HashSet<>();
        for(int k = 0; k < 4; k++){
            int nx = i + idx[k][0], ny = j + idx[k][1];
            if(nx < 0 || nx >= m || ny < 0 || ny >= n || grid[nx][ny] == 0) continue;
            int mark = grid[nx][ny];
            if(!set.contains(mark)){
                ans += map.get(mark);
                set.add(mark);
            }
        }
        return ans;
    }
    public int dfs(int i, int j, int mark){
        if(i < 0 || i >= m || j < 0 || j >= n || visited[i][j] || grid[i][j] != 1){
            return 0;
        }
        visited[i][j] = true;
        int ans = 1;
        grid[i][j] = mark;
        for(int k = 0; k < 4; k++){
            int nx = i + idx[k][0], ny = j + idx[k][1];
            ans += dfs(nx, ny, mark);
        }
        return ans;
    }
}