近邻算法,特别是K-近邻算法(K-Nearest Neighbors, KNN),是一种基于实例的学习方法,广泛应用于分类和回归分析任务。下面是K-近邻算法的详细说明:
基本概念
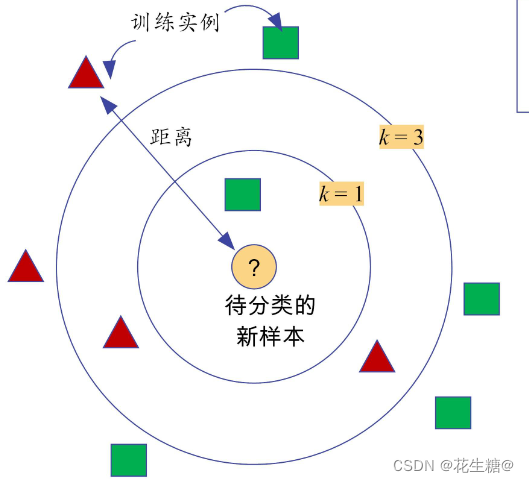
K-近邻算法的核心思想是“物以类聚”,即一个对象的类别可以通过它周围最相似对象的类别来决定。它假设相似的数据点应该属于同一类别。
工作流程
-
数据准备:首先,收集并整理数据集,其中包括已知类别标签的训练样本。每个样本都有多个特征,这些特征用来描述样本的属性。
-
选择距离度量:确定如何衡量两个数据点之间的相似度。常见的距离度量方法有欧氏距离、曼哈顿距离、切比雪夫距离等。距离越小,表示两个样本越相似。
-
确定K值:K是一个预先设定的正整数,表示在预测时考虑的最近邻居的数量。K值的选择会影响算法的性能,通常通过交叉验证来确定最佳K值。
-
预测过程:
- 对于一个新的未知类别的样本点,计算它与训练集中每个样本的距离。
- 找出距离最近的K个训练样本,这些就是最近邻。
- 分析这K个邻居的类别,根据多数表决原则(分类任务)或平均值(回归任务)来预测新样本的类别或值。
优缺点
-
优点:
- 理论简单,易于理解和实现。
- 对异常值不敏感,因为基于多数投票,少数异常点的影响有限。
- 无需训练阶段,预测时才进行计算,因此适合实时预测系统。
-
缺点:
- 计算量大,尤其是在大数据集上,每次预测都需要计算与所有训练样本的距离。
- 对于高维数据,距离度量可能失去意义(维度诅咒)。
- 需要存储整个训练数据集,空间开销大。
- 选择合适的K值和距离度量方法对性能影响显著,且依赖于具体问题。
应用
KNN因其简单有效,广泛应用于模式识别、推荐系统、图像识别、医学诊断、金融风险评估等多个领域。
改进与扩展
为了克服KNN的一些缺点,研究者提出了多种改进方法,比如权重KNN(考虑距离远近给予不同的权重)、增量学习、使用KD树或Ball Tree等数据结构进行高效索引,以及降维技术来缓解维度诅咒问题。