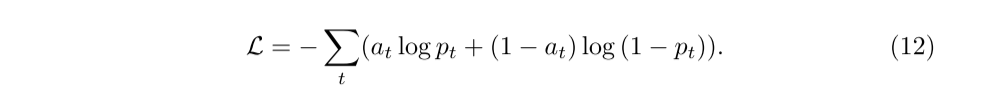摘要
随着在线教育的快速发展,知识追踪(KT)已成为追踪学生知识状态并预测他们在新问题上的表现的基本问题。在线教育系统中的问题通常很多,并且总是与更少的技能相关联。然而,以往的文献未能将问题信息与高阶问题-技能相关性结合起来,这主要受到数据稀疏性和多技能问题的限制。从模型的角度来看,以前的模型很难捕捉到学生运动历史的长期依赖性,也无法以一致的方式对学生问题和学生技能之间的相互作用进行建模。在本文中,我们提出了一种基于图的知识追踪交互模型(GIKT)来解决上述问题。更具体地说,GIKT 利用图卷积网络 (GCN) 通过嵌入传播充分结合问题和技能的相关性。此外,考虑到相关问题通常分散在整个练习历史中,而问题和技能只是知识的不同实例,GIKT将学生对问题的掌握程度概括为学生当前状态、学生相关学习记录、目标问题和相关技能之间的相互作用。三个数据集上的实验表明,GIKT 实现了新的最先进的性能,至少有 1% 的绝对AUC提高。
介绍
在MOOC或智能辅导系统等在线学习平台中,知识追踪(KT)是一项必不可少的任务,旨在追踪学生的知识状态。在口语层面上,KT解决了预测学生能否根据以前的学习经历正确地回答新问题。KT任务已被广泛研究,并提出了各种方法来处理它。
现有的KT方法通常基于目标问题对应的技能而不是问题本身来构建预测模型。在KT任务中,存在多个技能和许多问题,其中一个技能与许多问题相关,一个问题可能对应多个技能,可以用关系图表示,如图1所示的示例。由于假设技能的掌握可以在一定程度上反映学生是否能够正确回答相关问题,因此根据技能进行预测是一种可行的替代方案, 就和以前的KT方法一样。
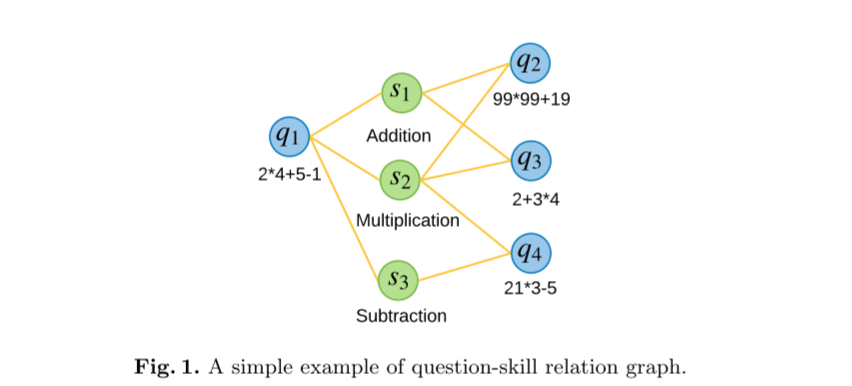
尽管这些仅仅基于技能的KT方法取得了实证成功,但问题的特征被忽视了,这可能会导致性能下降。例如,在图 1 中,即使 q2 和 q3 这两个问题具有相同的技能,但它们不同的难度可能会导致正确回答的概率不同。为此,之前的几部作品利用问题特征作为技能输入的补充。然而,由于问题的数量通常很大,而许多学生只尝试一小部分问题,大多数问题只能由少数学生回答,从而导致数据稀疏性问题。此外,对于那些共享部分共同技能的问题(例如q1和q4),简单地增加问题特征会丢失潜在的问题间和技能间的信息。基于这些考虑,利用问题和技能之间的高阶信息非常重要。
在本文中,我们首先研究如何有效地提取问题-技能关系图中包含的高阶关系信息。图神经网络 (GNN) 通过聚合来自邻居的信息来提取图所表示的信息, 提供了强大推动作用,我们利用图卷积网络 (GCN) 来学习问题和技能的嵌入高阶关系。一旦问题和技能嵌入被聚合,我们可以直接将问题嵌入与相应的答案嵌入一起作为 KT 模型的输入。
嵌入(Embedding)是一种分布式表示方法,即把原始输入数据分布地表示成一系列特征的线性组合
除了输入特征,KT 中另一个关键问题是模型框架。深度学习的最新进展模拟了一系列卓有成效的深度 KT 作品,这些作品利用深度神经网络顺序捕捉学生知识状态的变化。两个具有代表性的深度 KT 模型是深度知识追踪 (DKT) 和动态键值记忆网络 (DKVMN) ,它们分别利用递归神经网络 (RNN) 和记忆增强神经网络 (MANN) 来解决KT。然而,众所周知,它们无法捕获问题串中的长期依赖关系。为了解决这个问题,顺序键值记忆网络 (SKVMN) 提出了一种 hop-LSTM 架构,该架构将相似的练习和隐藏状态聚合为一个新状态,并提出了具有注意机制的练习增强循环神经网络 (EERNNA) 使用注意力机制对所有历史状态进行加权求和聚合。
我们进一步改善了长期依赖捕获和更好地建模学生的掌握程度,而不是将相关的历史信息聚合到一个新的状态中进行预直接用词。受 SKVMN 和 EERNNA 的启发,我们引入了一个回顾(recap)模块,根据注意力权重选择几个最相关的隐藏练习,以达到降噪的目的。考虑到对新问题及其相关技能的掌握,我们推广了交互模块,并将相关练习和当前隐藏状态与聚合的问题嵌入和技能嵌入进行交互。推广后的交互模块可以更好地模拟学生对问题和技能的掌握程度。此外,注意力机制应用于每个交互以做出最终预测,该机制自动对所有交互的预测效用进行加权。
综上所述,在本文中,我们提出了一个端到端的深度框架,即基于图的知识追踪交互(GIKT),用于知识追踪。我们的主要贡献总结如下:
通过利用图卷积网络聚合问题嵌入和技能嵌入,GIKT能够利用高阶问题-技能关系,从而缓解数据稀疏问题和多技能问题。
在交互模块之后引入recap模块,我们的模型可以更好地以一致的方式模拟学生对新问题及其相关技能的掌握程度。
根据经验,我们对三个基准数据集进行了扩展实验,结果表明我们的 GIKT 大幅优于最先进的基线。
相关工作
知识追踪
现有的知识追踪方法大致可以分为两类: 传统的机器学习方法和深度学习方法。本文主要研究深度KT方法。
传统的机器学习 KT 方法主要涉及两种类型:贝叶斯知识追踪(BKT)和因子分析模型。
BKT 是一种隐马尔可夫模型,它将每个技能视为一个二元变量,并使用贝叶斯规则来更新状态。几项工作扩展了vanilla BKT模型, 以更多信息纳入其中,例如失误和猜测概率、技能难度和学生个性化。另一方面,因子分析模型侧重于从历史数据中学习一般参数以进行预测。
在因子分析模型中,项目反应理论 (IRT) 为学生能力和问题难度建模参数,绩效因素分析 (PFA) 考虑了技能和知识追踪机的积极和消极反应的数量利用分解机将问题和用户的辅助信息编码到参数模型中。
最近,由于巨大的容量和有效的表示学习,KT 文献中已经利用了深度神经网络。深度知识追踪(DKT)是第一个深度知识追踪方法,它使用循环神经网络(RNN)来追踪学生的知识状态。动态键值记忆网络 (DKVMN) 可以发现每个技能的基本概念并跟踪每个概念的状态。基于这两个模型,已经提出了几种考虑更多信息的方法,例如学生的遗忘行为,被专家标记过的多技能信息、必备技能关系图和学生个性化。GKT构建技能关系图并明确学习它们的关系。然而,这些方法仅使用技能作为输入,这会导致信息丢失。
一些深度 KT 方法在预测中考虑了问题特征。记忆网络动态学生分类(DSCMN)利用问题难度来帮助区分与相同技能相关的问题。具有注意力机制的运动增强循环神经网络(EERNNA)使用问题的内容对问题嵌入进行编码,使问题嵌入可以包含问题的特征信息,但实际上很难收集问题的内容。由于数据稀疏性问题,DHKT通过使用问题和技能之间的关系来增强 DKT 来获得问题表示,但是,这未能捕获问题间和技能间的关系。在本文中,我们使用 GCN 来提取问题-技能图中包含的高阶信息。为了处理长期依赖性问题,顺序键值记忆网络 (SKVMN)使用带有跳跃的改进 LSTM 来增强捕获练习串行中长期依赖性的能力。 EERNNA假设当前学生的知识状态是所有历史学生状态的加权和聚合,基于当前问题和历史问题之间的相关性。我们的方法与这两项工作的不同之处在于它们将相关的隐藏状态聚合到一个新的状态中进行预测,而我们首先选择最有用的历史练习来减少噪声对当前状态的影响,然后我们执行成对交互以进行预测。
图神经网络
近年来,图数据在深度学习模型中得到广泛应用。然而,传统的神经网络存在复杂图的非欧结构。受 CNN 的启发,一些作品对图结构数据使用卷积方法。图卷积网络建议被用于(GCNs)半监督图分类,它根据自身及其邻居更新节点表示。这样,如果使用多个图卷积层,更新的节点表示包含邻居节点的属性和高阶邻居的信息。由于 GCN 的巨大成功,针对图数据进一步提出了一些变体。随着图神经网络(GNN)的发展,许多应用基于 GNN 的算法出现在各个领域,例如自然语言处理 (NLP)、计算机视觉(CV)和推荐系统。由于GNN有助于捕获高阶信息,我们在 GIKT 模型中使用 GCN 将技能和问题之间的关系提取到它们的表示中。据我们所知,我们的方法 GIKT 是第一个通过图形神经网络对问题技能关系进行建模的方案。
初步工作
知识追踪: 在知识追踪任务中,学生依次回答在线学习平台提供的一系列问题。学生回答每个问题后,将发出答案是否正确的反馈。在这里,我们将练习表示为 xi = (qi, ai), 其中 qi 是问题ID,ai ∈ {0, 1} 表示学生是否正确回答了 qi。给定一个练习序列 X = {x1, x2, ..., xt−1} 和新问题 qt,KT 的目标就是预测学生正确回答它的概率 p(at = 1|X, qt)。
问题-技能关系图: 每个问题对应一个或多个技能{s1, ..., sni},而一项技能 sj 通常与许多问题 {q1、...、qnj} 相关,其中 ni 是与问题 qi 相关的技能数量, nj 是与技能 sj 相关的问题数量。这里我们将关系表示为问题-技能关系二分图 G,定义为 { (q, rqs, s) | q ∈ Q, s ∈ S},其中 Q 和 S 分别对应于问题和技能集合。如果问题q与技能s相关,则rqs = 1。
GIKT方案
在本节中,我们将详细介绍我们的方法,整体框架如图 2 所示:
GCN: 学习问题-技能关系图上聚合的问题和技能表示
RNN: 模拟知识状态的顺序变化
回顾 (Recap) 模块: 捕获长期依赖性并全面利用有用的信息
交互 (Interaction) 模块: 进行最终预测
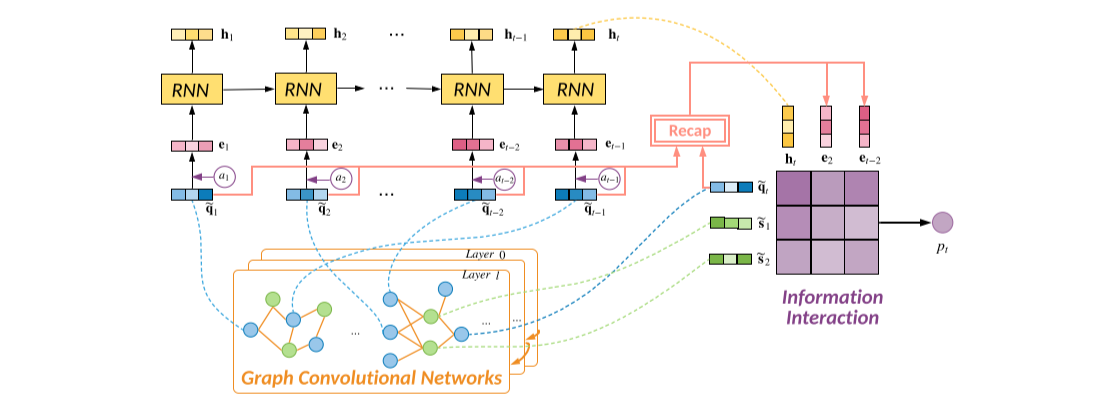
图2: GIKT在时间步骤t的图示,其中qt是新问题。首先,我们使用GCN来聚合问题和技能嵌入。然后使用RNN对顺序知识状态ht进行建模。在回顾模块中, 我们选择了与qt最相关的隐藏练习,它对应于软选择和硬选择实现。信息交互模块在学生当前状态、所选学生历史练习、目标问题和相关技能之间进行成对交互,以进行预测。
嵌入层
我们的GIKT方法使用嵌入来表示问题,技能和答案。三个嵌入矩阵 Es ∈ R(|S|×d), Eq ∈ R(|Q|×d), Ea ∈ R(2×d)表示查找操作,其中 d 代表嵌入大小。Es 或 Eq 中的每一行对应一个技能或一个问题。Ea中的两行分别表示错误和正确答案。对于矩阵中的第 i 行向量,我们分别使用 si、qi 和 ai 来表示它们。
在我们的框架中,我们不预训练这些嵌入,它们通过以端到端的方式,在优化最终目标时才被训练。
嵌入传播
从训练的角度来看,问题数据的稀疏性是对学习信息丰富的问题的巨大挑战,尤其是对于那些训练示例非常有限的问题。从推理的角度看,学生能否正确回答新问题,取决于其相关技能的掌握情况和问题的特点。当Ta以前解决过类似问题时,Ta更有可能正确回答新问题。在这个模型中,我们结合了问题-技能关系图 G 来解决稀疏性问题,并利用先验相关性来获得更好的问题表示。
考虑到问题-技能关系图是二分的,一个问题的第一跳邻居应该是它对应的技能,第二跳邻居应该是共享相同技能的其他问题。为了提取高阶信息,我们利用图卷积网络 (GCN) 将相关技能和问题编码为问题嵌入和技能嵌入。
图卷积网络堆叠多个图卷积层来编码高阶邻居信息,并且在每一层中,节点表示可以通过自身和邻居节点的嵌入来更新。将图中节点i的表示表示为xi(xi 可以表示技能嵌入si或问题嵌入 qi), 将其邻居节点的集合表示为 Ni,则第 l 层 GCN 层的公式可以表示为:
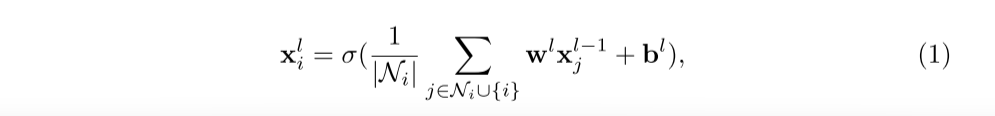
其中 wl 和 bl 是第 l 个GCN层中要学习的总权重和偏差,σ是非线性变换,例如ReLU。通过 GCN 进行嵌入传播后,我们得到问题和技能。我们使用~q 和~s 来表示嵌入传播后的问题和技能表示。为了便于实现和更好的并行化,我们为每个批次采样固定数量的问题邻居 nq和技能邻居 ns。在推理过程中,我们多次运行每个示例(对不同的邻居进行采样),并将模型输出取平均,以获得稳定的预测结果。
学生状态演变
对于每个历史时间 t, 我们将问题和回答嵌入连接 (并不是将两个向量直接连在一起) 起来,并通过非线性变换投影到 d 维作为练习的表示, 这里我们使用[ ,]来表示向量连接:
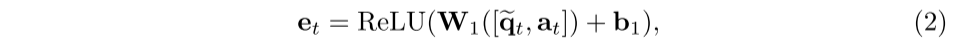
不同练习之间可能存在依赖关系,因此我们需要对整个练习过程进行建模,以捕捉学生状态的变化并了解练习之间的潜在关系。为了模拟学生做练习的顺序行为,我们使用 LSTM 从输入练习表示中学习学生状态:
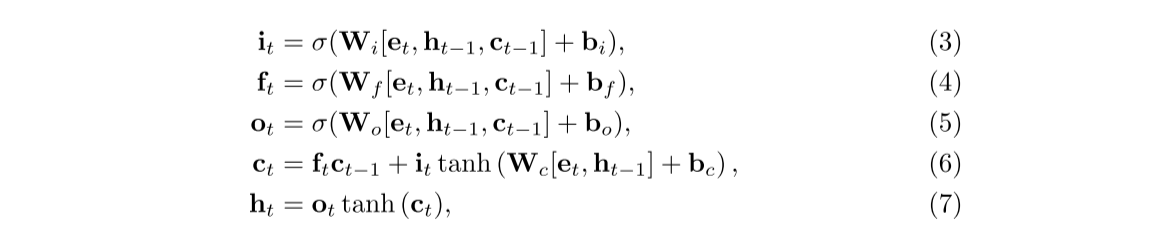
其中ht、ct、it、ft、ot分别表示隐藏状态、单元状态、输入门、遗忘门、输出门。值得一提的是,这一层对于捕捉粗粒度依赖关系 (例如技能之间的潜在关系等) 很重要,所以我们只是学习一个隐藏状态ht ∈ Rd 作为当前学生状态,其中包含技能的粗粒度掌握状态。
历史回顾模块
在学生的锻炼历史中,相关技能的问题很可能散落在很长的历史记录中。从另一个角度来看,连续的练习可能不会遵循一个连贯的主题。这些现象对传统 KT 方法中的 LSTM 串行建模提出了挑战:
众所周知,LSTM很难在很长的串行中捕获长期依赖关系,这意味着当前的学生状态ht可能会“忘记”与新目标问题qt相关的历史练习。
当前学生状态 ht 考虑更多关于最近的练习,这可能包含新目标问题 qt 的噪声信息。
当学生在回答一个新问题时,Ta可能会迅速回忆起Ta以前做过的类似问题,以帮助Ta理解新问题。受此行为启发,我们建议选择相关的历史练习(问题-答案对){ei | i ∈ [1, 2, ... , t − 1] } 以更好地表示学生在特定问题 qt 上的能力,即为历史回顾模块。
我们开发了两种方法来查找相关的历史练习。第一个是硬选择,即我们只考虑与新问题有相同技能的练习:
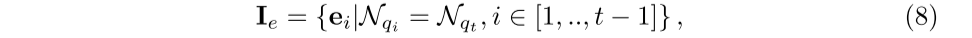
另一种方法是软选择,即我们通过注意力网络学习目标问题与历史状态之间的相关性,并选择top-k 注意力得分最高的状态:
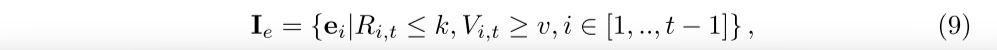
其中 Ri,t 是注意力函数 f(qi, qt) 的排名,就像余弦相似性一样,Vi,t 是注意力值,v 是过滤不太相关的练习的相似度下限。
广义交互模块
以前的KT方法主要根据学生状态 ht 和问题 qt, 即<ht, qt>之间的交互作用来预测学生的表现。我们将互动概括为以下几个方面:
我们用<ht, ~qt>来表示学生对问题qt的掌握程度程度,<ht, ~sj>来表示学生对相应技能的掌握程度sj ∈ Nqt,
我们将当前学生状态的互动推广到历史练习中,这反映了相关的历史掌握,即 <ei, ~qt> 和 <ei,~sj>, ei ∈ Ie,相当于让学生在历史时间步长中回答目标问题
我们尝试其他实现方法, 例如使用历史状态而不是历史练习, 结果表明使用 历史练习会产生更好的性能,因为历史状态包含其他不相关的信息。
然后我们考虑上述所有交互作用进行预测,并定义广义交互作用模块。为了促进相关交互并减少噪声,我们使用注意力网络来学习所有交互作用项的双注意力权重,并计算加权和作为预测:
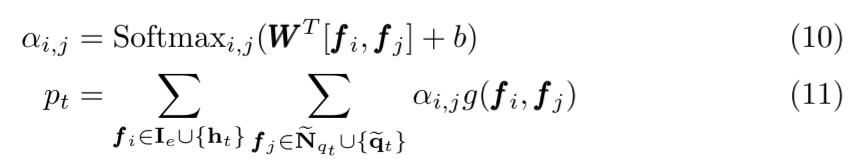
其中 pt 是正确回答新问题的预测概率,~Nqt 表示 qt 的聚合邻居技能嵌入,我们使用内积来实现函数 g。与在关系图中选择邻居类似,我们通过从这两个集合中采样来设置固定数量的 Ie 和 ~Nqt。
优化器
为了优化我们的模型,我们使用梯度下降法更新模型中的参数,通过最小化回答正确的预测概率和学生回答的真实标签之间的交叉熵损失来更新模型中的参数