填充(padding)
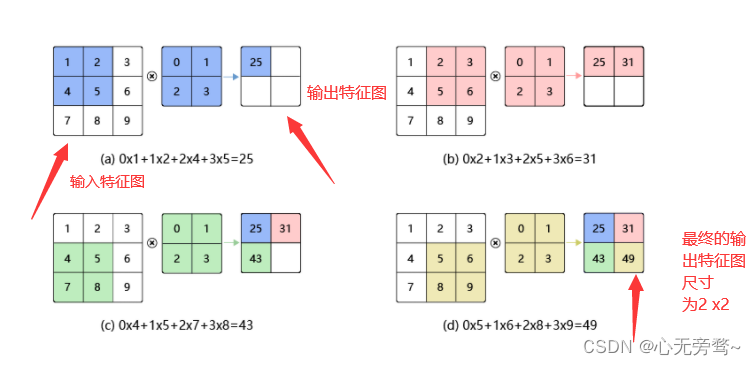
在上图中,输入图片尺寸为
3
×
3
3\times3
3×3,输出图片尺寸为
2
×
2
2\times2
2×2,经过一次卷积之后,图片尺寸为
2
×
2
2\times2
2×2,经过一次卷积之后,图片尺寸变小。卷积输出特征图的尺寸计算方法如下(卷积核的高和宽分别为
k
h
和
k
w
k_h和k_w
kh和kw):
H
o
u
t
=
H
−
k
h
+
1
W
o
u
t
=
W
−
k
w
+
1
H_{out}=H-k_h+1\\ W_{out}=W-k_w+1
Hout=H−kh+1Wout=W−kw+1
如果输入尺寸为4,卷积核大小为3时,输出尺寸为
4
−
3
+
1
=
2
4-3+1=2
4−3+1=2。读者可以自行检查当输入图片和卷积核为其他尺寸时,上述计算式是否成立。当卷积核尺寸大于1时,输出特征图的尺寸会小于输入图片尺寸。如果经过多次卷积,输出图片尺寸会不断减小。为了避免卷积之后图片尺寸变小,通常会在图片的外围进行填充(padding),如下图所示:
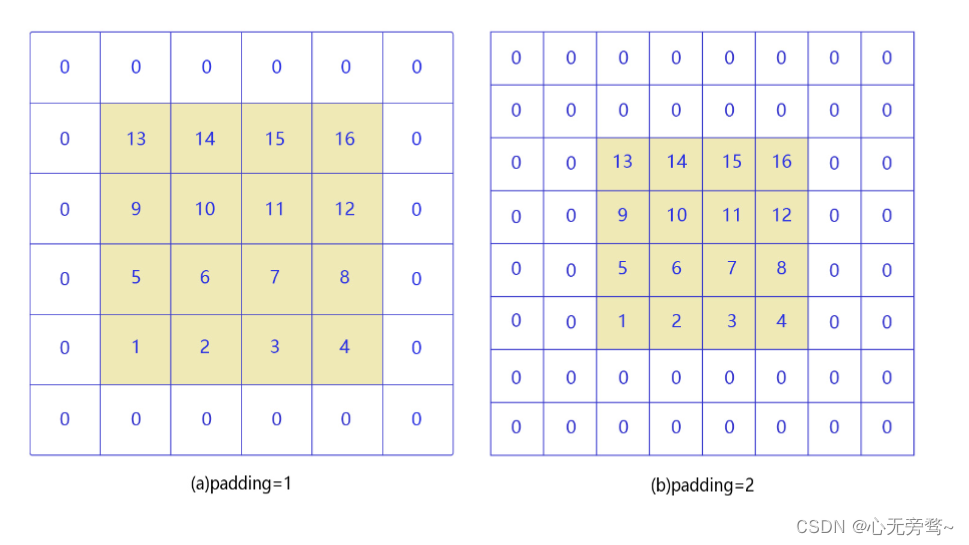
- 如图(a)所示:填充的大小为1,填充值为0。填充之后,输入图片尺寸从 4 × 4 4\times4 4×4变成了 6 × 6 6\times6 6×6,使用 3 × 3 3\times3 3×3的卷积核,输出图片尺寸为 4 × 4 4\times4 4×4。
- 如图(b)所示:填充的大小为2,填充值为0。填充之后,输入图片尺寸从 4 × 4 4\times4 4×4变成了 8 × 8 8\times8 8×8,使用 3 × 3 3\times3 3×3的卷积核,输出图片尺寸为 6 × 6 6\times6 6×6。
如果在图片高度方向,在第一行之前填充
p
h
1
p_{h1}
ph1行,在最后一行之后填充
p
h
2
p_{h2}
ph2行;在图片的宽度方向,在第1列之前填充
p
w
1
p_{w1}
pw1列,在最后1列之后填充
p
w
2
p_{w2}
pw2列;则填充之后的图片尺寸为
(
H
+
p
h
1
+
p
h
2
)
×
(
W
+
p
w
1
+
p
w
2
)
(H+p_{h1}+p_{h2})\times (W+p_{w1}+p_{w2})
(H+ph1+ph2)×(W+pw1+pw2)。经过大小为
k
h
×
k
w
k_h\times k_w
kh×kw的卷积核操作之后,输出图片的尺寸为:
H
o
u
t
=
H
+
p
h
1
+
p
h
2
−
k
h
+
1
W
o
u
t
=
W
+
p
w
1
+
p
w
2
−
k
w
+
1
H_{out}=H+p_{h1}+p_{h2}-k_h+1\\ W_{out}=W+p_{w1}+p_{w2}-k_w+1
Hout=H+ph1+ph2−kh+1Wout=W+pw1+pw2−kw+1
在卷积计算过程中,通常会在高度或宽度的两侧采取等量填充,即
p
h
1
=
p
h
2
=
p
h
,
p
w
1
=
p
w
2
=
p
w
p_{h1}=p_{h2}=p_h,p_{w1}=p_{w2}=p_w
ph1=ph2=ph,pw1=pw2=pw,所以上面的公式就变为了:
H
o
u
t
=
H
+
2
p
h
−
k
h
+
1
W
o
u
t
=
W
+
2
p
w
−
k
w
+
1
H_{out}=H+2p_h-k_h+1\\ W_{out}=W+2p_w-k_w+1
Hout=H+2ph−kh+1Wout=W+2pw−kw+1
卷积核大小通常使用1,3,5,7这样的奇数,如果使用的填充大小为
p
h
=
(
k
h
−
1
)
/
2
,
p
w
=
(
k
w
−
1
)
/
2
p_h=(k_h-1)/2,p_w=(k_w-1)/2
ph=(kh−1)/2,pw=(kw−1)/2,则卷积之后图像尺寸不变。
例如当卷积核大小为3时,padding大小为1,卷积之后图像尺寸不变,与图(a)一样;同理,如果卷积核大小为5,padding大小为2,也能保持图像尺寸不变。
步幅(stride)
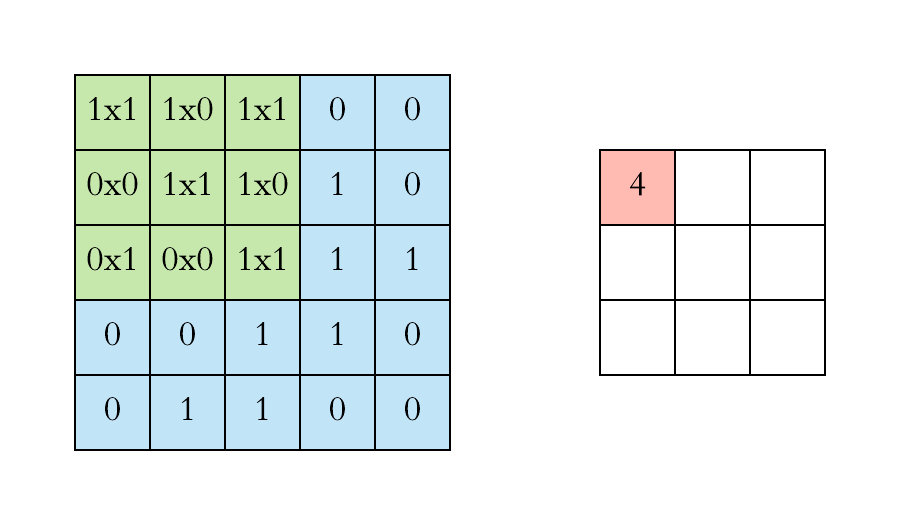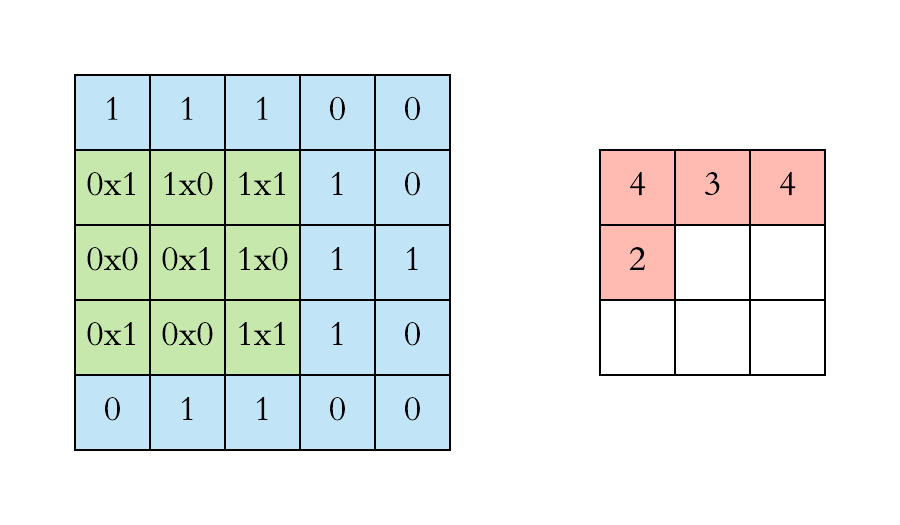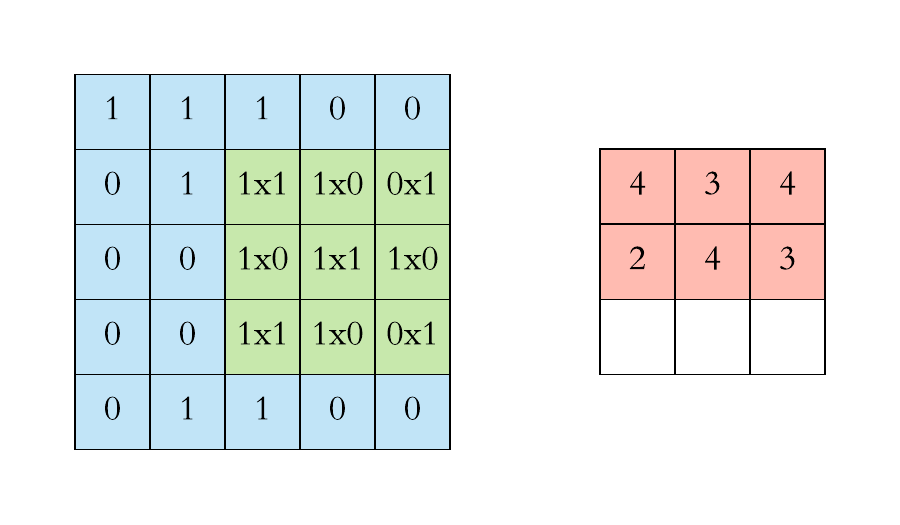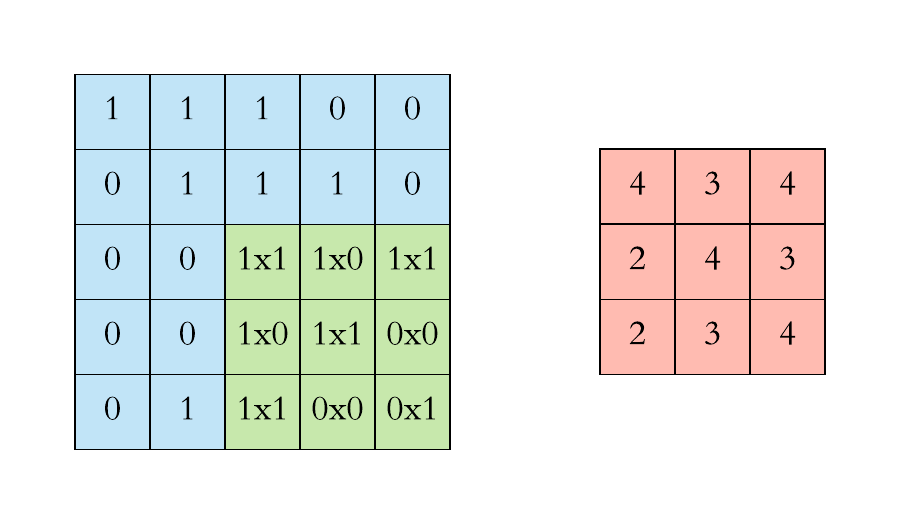
上图中卷积核每次滑动一个像素点,这是步幅为1的特殊情况,下面两张图是步幅为2的卷积过程,卷积核在图片上移动时,每次移动大小为2个像素点。


以第二张静态图为例子:
当宽和高的步幅分别为
s
h
和
s
w
s_h和s_w
sh和sw时,输出特征图尺寸的计算公式是:
H
o
u
t
=
H
+
2
p
h
−
k
h
s
h
+
1
W
o
u
t
=
W
+
2
p
w
−
k
w
s
w
+
1
H_{out}=\frac{H+2p_{h}-k_h}{s_h}+1\\ W_{out}=\frac{W+2p_w-k_w}{s_w}+1
Hout=shH+2ph−kh+1Wout=swW+2pw−kw+1
假设输入图片尺寸时
H
×
W
=
100
×
100
H\times W=100\times100
H×W=100×100,卷积核大小为
k
h
×
k
w
=
3
×
3
k_h\times k_w=3\times3
kh×kw=3×3,填充
p
h
=
p
w
=
1
p_h=p_w=1
ph=pw=1,步幅为
s
h
=
s
w
=
2
s_h=s_w=2
sh=sw=2,则输出特征图的尺寸为:
H
o
u
t
=
100
+
2
−
3
2
+
1
=
50
W
o
u
t
=
100
+
2
−
3
2
+
1
=
50
H_{out}=\frac{100+2-3}{2}+1=50\\ W_{out}=\frac{100+2-3}{2}+1=50
Hout=2100+2−3+1=50Wout=2100+2−3+1=50
总结:
1。卷积输出特征图的尺寸计算方法如下(卷积核的高和宽分别为 k h 和 k w k_h和k_w kh和kw): H o u t = H − k h + 1 W o u t = W − k w + 1 H_{out}=H-k_h+1\\ W_{out}=W-k_w+1 Hout=H−kh+1Wout=W−kw+1
2。当宽和高的步幅分别为 s h 和 s w s_h和s_w sh和sw时,输出特征图尺寸的计算公式是:
H o u t = H + 2 p h − k h s h + 1 W o u t = W + 2 p w − k w s w + 1 H_{out}=\frac{H+2p_{h}-k_h}{s_h}+1\\ W_{out}=\frac{W+2p_w-k_w}{s_w}+1 Hout=shH+2ph−kh+1Wout=swW+2pw−kw+1